Tóm tắt tài liệu
Sau khi đọc bài viết công thức logarit thì có lẽ các em đã làm quen với các khái niệm và định nghĩa logarit. Để hiểu hơn về chuyên đề này, đặc biệt là dạng bài tập tìm nghiệm của bất phương trình, các em hãy tìm hiểu trong bài viết này nhé. Bài viết tổng hơp khá nhiều bài tập về bất phương trình logarit. Các bài toán mang tính đặc trưng và phổ biến cho toàn dạng.
Phương pháp sử dụng biến đổi tương đương
Để giải bất phương trình Loga loại khó, điều đầu tiên cũng là quan trọng nhất, các em cần nắm vững cách giải của các loại bài tập cơ bản (bất phương trình cơ bản có chứa biểu thức logarit)
+) Dạng toán: logax > b (a>0)
+) Cách giải: Chia thành 2 trường hợp theo các khoảng của a. Mỗi trường hợp sẽ có cách giải riêng như ở dưới đây
-
Nếu a>1
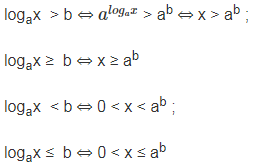
-
Nếu 0<a<1
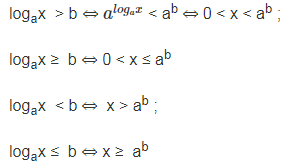
Dạng toán này gồm 2 loại:
- Loại 1: Cơ số là một hằng số
- Loại 2: Khi cơ số là một hàm của x
Sử dụng phương pháp logarit hóa và đưa về cùng cơ số
Để chuyển ẩn số khỏi số mũ luỹ thừa người ta có thể logarit theo cùng 1 cơ số cả 2 vế của phương trình, ta có
các dạng
- Dạng 1: Phương trình:
- Dạng 2: Phương trình: (cơ số khác nhau và số mũ khác nhau)
Sử dụng phương pháp đặt ẩn phụ
Phương pháp dùng ẩn phụ dạng 1 là việc sử dụng 1 ẩn phụ để chuyển phương trình ban đầu thành 1 phương
trình với 1 ẩn phụ.
Ta lưu ý các phép đặt ẩn phụ thường gặp sau:
- Dạng 1: Phương trình đặt ẩn phụ
- Dạng 2: Phương trình đặt cụm ẩn phụ
Sau khi nắm vững cách giải của bất phương trình cơ bản có chứa biểu thức logarit, các em có thể thực hành các bài toán khó hơn với lưu ý: Chuyển tư dạng phức tạp thành dạng cơ bản. Hãy cùng xem xét một số bài tập sau đây để có thể hiểu hơn về phương pháp giải bài toán này.
Xem thêm: Bất phương trình lượng giác
Bài tập bất phương trình logarit có lời giải
Dưới đây là các phương pháp giải cũng như bài tập thực hành cực kì chi tiết về chuyên đề mũ và logarit. Các bài tập mũ và logarit có sự chuyển hóa hỗ trợ nhau rất tốt, do đó để làm tốt các bài tập về phương trình logarit hay bất phương trình, các em cần phải nắm rõ kiến thức của hàm số mũ. Đó là lý do tài liệu này được lồng ghép hai kiến thức lại với nhau.
Cảm ơn các bạn đã xem bài viết bất phương trình logarit – Phương pháp giải và bài tập, mong rằng qua bài viết này có thể đem lại cho các bạn nhiều kiến thức nhất về chuyên đề này. Bạn có thể xem tài liệu tương tự, cùng chủ đề ở phía cuối trang.
Xem thêm: Bất phương trình chứa căn




 056.3753648
056.3753648
 Chat FB
Chat FB