Tóm tắt tài liệu
Để thuận tiện cho việc tra cứu và học thuộc, chúng tôi đã tổng hợp các công thức logarit và công thức mũ và công thức lũy thừa vào các bảng dưới đây. Mong rằng đây sẽ là một bộ tài liệu hiệu quả, giúp các em có thể thuận tiện tra cứu bất cứ khi nào. Để nhớ các công thức dưới đây, các em có thể in công thức này ra, sau đó làm bài tập chứa các công thức này thật nhiều, ôn lại vào mỗi tuần và trước khi thi. Đảm bảo sẽ nhớ cực lâu… đây chính là phương pháp mà các bạn học sinh giỏi chia sẽ. Chúc các em thành công nhé.
1. Bảng công thức logarit
| CÔNG THỨC LOGARIT | |
| 1. \[{{\log }_{a}}1=0\] | 8. \[{{\log }_{a}}{{N}^{2}}=2.{{\log }_{a}}\left| N \right|\] |
| 2. \[{{\log }_{a}}a=1\] | 9. \[{{\log }_{a}}N={{\log }_{a}}b.{{\log }_{b}}N\] |
| 3. \[{{\log }_{a}}{{a}^{m}}=m\] | 10. \[{{\log }_{a}}N=\frac{{{\log }_{a}}N}{{{\log }_{a}}b}\] |
| 4. \[{{a}^{{{\log }_{a}}n}}=n\] | 11. \[{{\log }_{a}}b=\frac{1}{{{\log }_{a}}b}\] |
| 5. \[{{\log }_{a}}({{n}_{1}}.{{n}_{2}})={{\log }_{a}}{{n}_{1}}+{{\log }_{a}}{{n}_{2}}\] | 12. \[{{\log }_{{{a}^{\alpha }}}}N=\frac{1}{\alpha }.{{\log }_{a}}N\] |
| 6. \[{{\log }_{a}}\left( \frac{{{n}_{1}}}{{{n}_{2}}} \right)={{\log }_{a}}{{n}_{1}}-{{\log }_{a}}{{n}_{2}}\] | 13. \[{{a}^{{{\log }_{b}}c}}={{c}^{{{\log }_{b}}a}}\] |
| 7. \[{{\log }_{a}}{{N}^{\alpha }}=\alpha .{{\log }_{a}}N\] | 14. \[{{\log }_{a}}x=\frac{{{\log }_{b}}x}{{{\log }_{b}}a}\] |
2. Bảng công thức mũ
| Công thức mũ | ||
| 1. \[{{a}^{m}}.{{a}^{n}}={{a}^{m+n}}\] | 6. \[\sqrt[n]{{{a}^{n}}}=\left\{\begin{matrix}a,n=2k+1 \\\left| a \right|,n=2k \\\end{matrix} \right.\] | 11. \[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\] |
| 2. \[{{(a.b)}^{n}}={{a}^{n}}.{{b}^{n}}\] | 7. \[\sqrt[n]{ab}=\sqrt[n]{a}.\sqrt[n]{b}\] | 12. \[\sqrt[n]{a}=\sqrt[mn]{{{a}^{m}}}\] |
| 3. \[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}}\] | 8. \[\sqrt[n]{{{a}^{p}}}={{\left( \sqrt[n]{a} \right)}^{p}}\] | 13. \[\sqrt[n]{{{a}^{m}}}={{a}^{\frac{m}{n}}},n>0\] |
| 4. \[{{\left( \frac{a}{b} \right)}^{n}}=\frac{{{a}^{n}}}{{{b}^{n}}}\] | 9. \[{{a}^{-\frac{m}{n}}}=\frac{1}{{{a}^{\frac{m}{n}}}}=\frac{1}{\sqrt[n]{{{a}^{m}}}}\] | 14. \[{{a}^{-n}}=\frac{1}{{{a}^{n}}}\] |
| 5. \[{{({{a}^{m}})}^{n}}={{({{a}^{n}})}^{m}}={{a}^{m.n}}\] | 10. \[\sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}\] | 15. \[\sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}\] |
3. Công thức lũy thừa
4. Công thức mở rộng
4.1. Công thức phương trình, bất phương trình mũ:
– \[{{a}^{f(x)}}={{a}^{g(x)}}\Leftrightarrow f(x)=g(x)\]
– \[{{a}^{f(x)}}=b={{a}^{{{\log }_{a}}b}}\Leftrightarrow f(x)={{\log }_{a}}b\]
– \[{{a}^{f(x)}}={{b}^{g(x)}}\Leftrightarrow f(x)=g(x).{{\log }_{a}}b\]
– \[{{a}^{f(x)}}>{{a}^{g(x)}}(1)\]
+) \[a>1\], \[(1)\Leftrightarrow f(x)>g(x)\]
+) \[0<a<1\], \[(1)\Leftrightarrow f(x)<g(x)\]
4.2. Phương trình logarit, bất phương trình logarit
– Vơi \[a>1\], \[{{\log }_{a}}f(x)>lo{{g}_{a}}g(x)\], \[\Leftrightarrow \left\{ \begin{matrix}f(x)>g(x) \\g(x)>0 \\\end{matrix} \right.\]
– Với \[0<a<1\], \[{{\log }_{a}}f(x)>lo{{g}_{a}}g(x)\], \[\Leftrightarrow \left\{ \begin{matrix}f(x)<g(x) \\f(x)>0 \\\end{matrix} \right.\]
– Xét bất phương trình: \[{{\log }_{a}}f(x)>b(1)\] với \[0<x\ne 1\]
+) Khi \[a>1\], \[(1)\Leftrightarrow f(x)>{{a}^{b}}\]
+) Khi \[0<a<1\], \[(1)\Leftrightarrow 0<f(x)<{{a}^{b}}\]
5. Tổng hợp tên gọi các công thức mũ, logarit, lũy thừa được đề cập trong bài viết
– Logarit của 1 thương: \[{{\log }_{a}}\left( \frac{{{n}_{1}}}{{{n}_{2}}} \right)={{\log }_{a}}{{n}_{1}}-{{\log }_{a}}{{n}_{2}}\]
– Logarit của 1 tích: \[{{\log }_{a}}({{n}_{1}}.{{n}_{2}})={{\log }_{a}}{{n}_{1}}+{{\log }_{a}}{{n}_{2}}\]
– Logarit tự nhiên: Kí hiệu là \[\ln \] và hiểu rằng: \[\operatorname{lnb}=lo{{g}_{e}}b\]
– Logarit nepe: được hiểu là một cái tên khác của logarit tự nhiên, kí hiệu \[\ln \]
– Logarit cơ số e: được hiểu là một cái tên khác của logarit tự nhiên, nhưng với ý nghĩa trực quan, dễ nhớ hơn.
– Logarit cơ bản: Các công thức trong bảng 1 và bảng 2 đều là những công thức cơ bản thường gặp trong các phép biến đổi đơn giản trong bài toán.
– Công thức đổi cơ số logarit: \[{{\log }_{a}}x=\frac{{{\log }_{b}}x}{{{\log }_{b}}a}\]
Bạn còn biết công thức logarit và công thức mũ nào khác không? Hãy bình luận bên dưới để bài viết thêm phong phú kiên thức nhé? Để giúp các em học sinh có thể nhớ công thức logarit và công thức mũ một cách tự nhiên nhất, chúng tôi đã tổng hợp 2 tài liệu sau để phục vụ các em:
6. Một số phương trình logarit cơ bản:
Khi giải phương trình logarit loại cơ bản ta thực hiện theo các bước sau:
+ Tìm điều kiện xác định: Đây là một bước khá quan trọng, khi điều kiện chưa chặt chẽ, kết quả của bài toán dễ bị loại bỏ. Hàm số logarit có điều kiện xác định khá khó chịu.
+ Dùng các phép biến đổi tương đương, áp dụng công thức logarit để biến đổi tương đương. Các phương trình hệ quả sau cùng có thể là phương trình bậc nhất, bậc 2, bậc 3 hoặc phương trình vô tỉ. Chúng ta cùng tham khảo một số ví dụ sau để có thể dễ dàng hình dung hơn:
1. \[{{\log }_{3}}(3x-2)=3\]
– Điều kiện: \[x>\frac{2}{3}\]
– Giải: \[{{\log }_{3}}(3x-2)=3\] \[\Leftrightarrow 3x-2={{3}^{3}}\] \[\Leftrightarrow x=\frac{29}{3}(TM)\]
2. \[{{\log }_{2}}({{\log }_{4}}x)=1\]
– Điều kiện: \[\left\{ \begin{matrix}x>0 \\{{\log }_{4}}x>0 \\\end{matrix} \right.\] \[\Leftrightarrow \left\{ \begin{matrix}x>0 \\x>1 \\\end{matrix} \right.\] \[\Leftrightarrow x>1\]
– Giải: \[{{\log }_{2}}({{\log }_{4}}x)=1\] \[\Leftrightarrow {{\log }_{4}}x=2\] \[\Leftrightarrow x={{4}^{2}}=16\] (TM)
3. \[{{\log }_{\sqrt{3}}}\left| x+1 \right|=2\]
– Điều kiện: \[\left| x+1 \right|>0\] \[\Leftrightarrow x\ne -1\]
– Giải: \[{{\log }_{\sqrt{3}}}\left| x+1 \right|=2\] \[\Leftrightarrow \left| x+1 \right|=3\] \[\Leftrightarrow \left[ \begin{matrix}x+1=3 \\x+1=-3 \\\end{matrix}, \right.\] \[\Rightarrow S=\left\{ -4;2\} \right.\]
4. Giải phương trình: \[{{\log }_{x}}(x+2)=2\]
– Điều kiện: \[\left\{ \begin{matrix}x+2>0 \\x>0 \\x\ne -1 \\\end{matrix},\Leftrightarrow \left\{ \begin{matrix}x>-2 \\x>0 \\x\ne -1 \\\end{matrix},\Leftrightarrow \right. \right.\left\{ \begin{matrix}x>0 \\x\ne -1 \\\end{matrix} \right.\]
– Giải: \[{{\log }_{x}}(x+2)=2,\Leftrightarrow x+2={{x}^{2}},\Leftrightarrow \left[ \begin{matrix}x=1(TM) \\
x=-1(KTM) \\\end{matrix}, \right.S=\text{ }\!\!\{\!\!\text{ }1\}\]
6. Một số phương trình mũ cơ bản
Về phương pháp giải loại phương trình này, không khác quá nhiều so với loại phương trình logarit mà mục 5 chúng ta đã tìm hiểu. Một số ví dụ sau đây sẽ giúp các bạn hiểu rõ hơn:
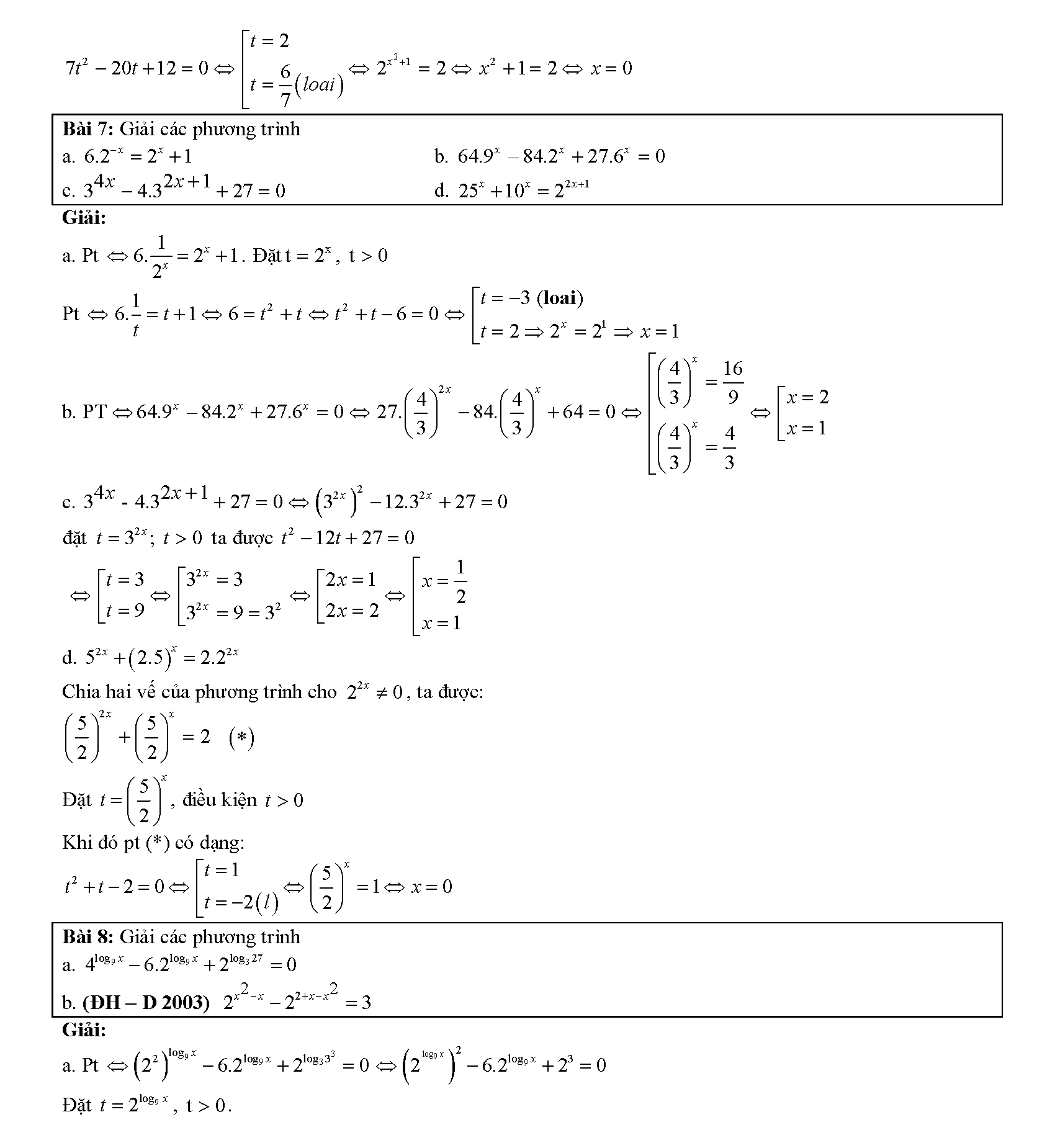
Vậy là chúng ta vừa tìm hiểu xong bộ công thức logarit – công thức mũ – công thức lũy thừa. Để thuận tiện hơn cho việc học, bạn có thể tải bảng công thức mà chúng tôi đã tổng hợp. Công thức toán học là khô khan, tuy nhiên nếu nắm vững thì sẽ giúp các em giải quyết nhiều bài tập. Hiện tại chúng tôi đang tìm giáo viên dạy kèm tại nhà, nếu bạn muốn kiếm thêm thu nhập có thể liên hệ với chúng tôi tại địa chỉ email: admin@tailieure.com.
Xem thêm video
video trên Thầy Linh dạy toán
Ôn tập GK2 Toán 11 chương trình mới năm học 2024-2025
056.3753648
Chat FB