Tóm tắt tài liệu
Một trong những chuyên đề quan trọng trong chương 2 toán 10, hàm số bậc hai lớp 10 xoáy sâu vào nhiều vấn đề hơn hàm số bậc nhất rất là nhiều. Do đó, tài liệu dưới đây không chỉ trình bày cho các em về những vấn đề lý thuyết cơ bản mà nó còn trình bày rất nhiều dạng bài tập đặc trưng, quan trọng. Tải file về để có thể xem chi tiết và đầy đủ tài liệu nhé.
Xem thêm:
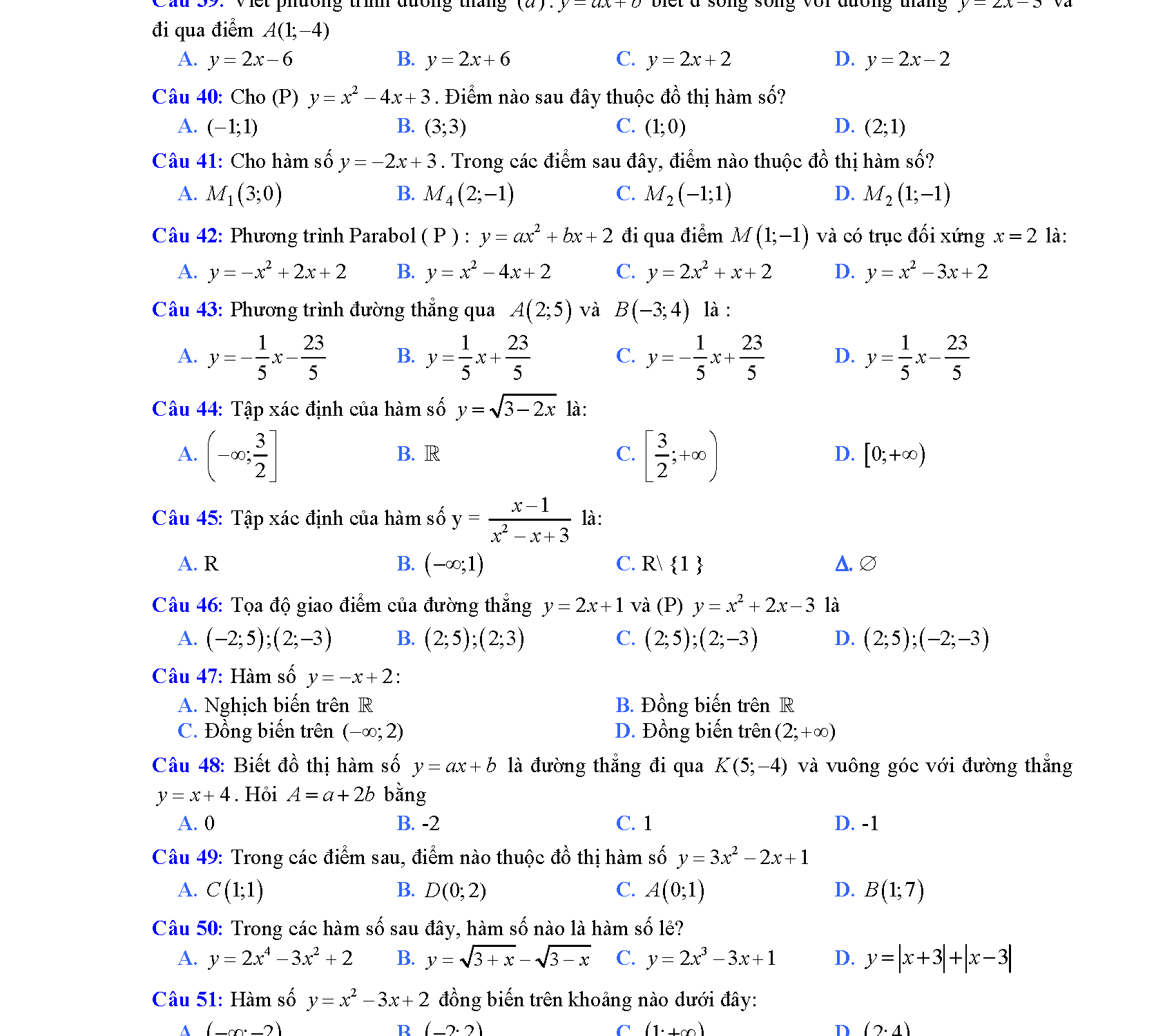
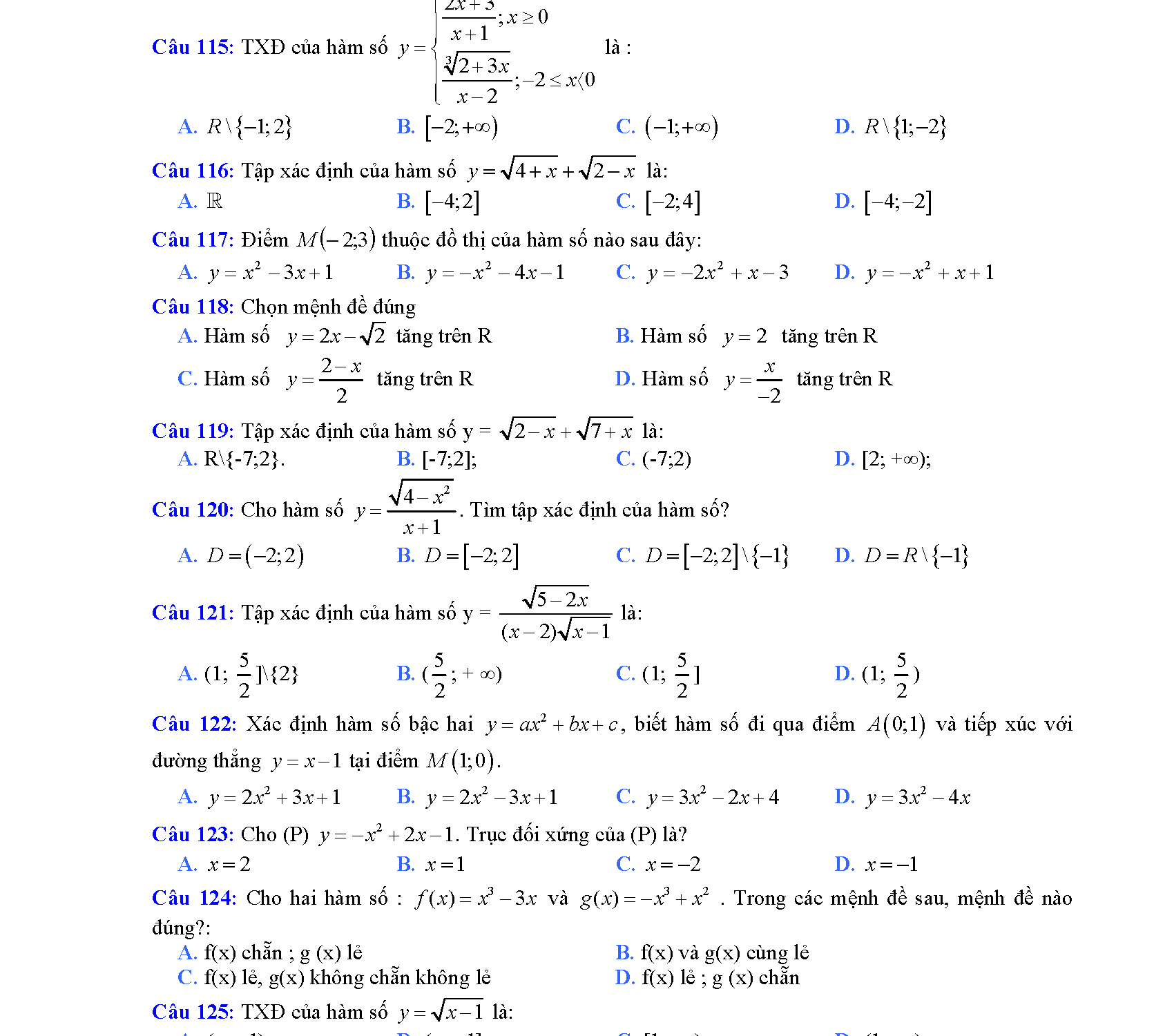
Lý thuyết hàm số bậc hai lớp 10
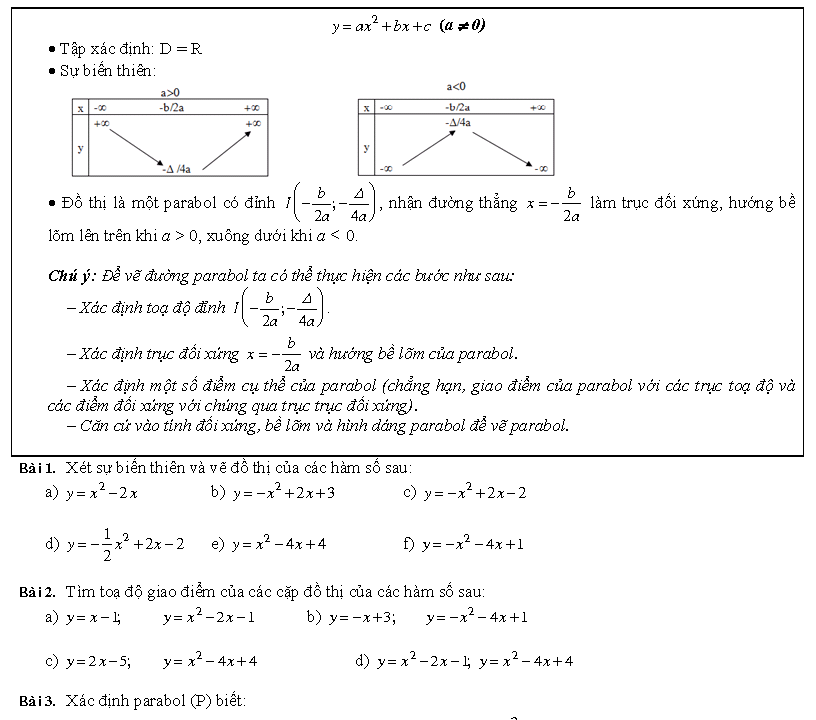
- Tập xác định: D = R
- Sự biến thiên:
Đồ thị là một parabol có đỉnh và nhận đường thẳng x = – b / 2a làm trục đối xứng, hướng bề lõm lên trên khi a > 0, xuông dưới khi a < 0.
Chú ý: Để vẽ đường parabol ta có thể thực hiện các bước như sau:
- Xác định toạ độ đỉnh
- Xác định trục đối xứng và hướng bề lõm của parabol.
- Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng).
- Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
Dạng 1: Xét sự biến thiên và vẽ đồ thị hàm số bậc hai
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
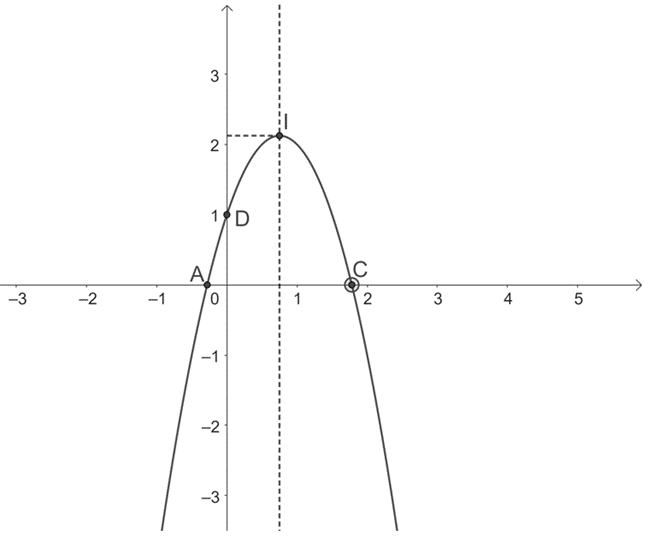
Dạng 2: Tương giao đồ thị hàm số
Tìm toạ độ giao điểm của các cặp đồ thị của các hàm số sau:
Dạng 3: Xác định hàm số bậc hai (Xác định Parabol)
Câu 1: Xác định Parabol (P) khi biết rằng:
- Đi qua điểm A(1; 0) và có trục đối xứng x = 3/2
- Đi qua điểm A(–1; 9) và có trục đối xứng x = -2
- Đi qua điểm A(0; 5) và có đỉnh I(3; –4).
- Đi qua điểm A(2; –3) và có đỉnh I(1; –4).
- Đi qua các điểm A(1; 1), B(–1; –3), O(0; 0).
- đi qua điểm A(1; 0) và đỉnh I có tung độ bằng –1.
Câu 2: Tìm Parabol (P): biết rằng
a) (P) đi qua A(0;-1) ; B(1;-1) ; C(-1;1).
b) (P) đi qua A(8;0) và có đỉnh I(6;-12)
Dạng 4: Vẽ đồ thị hàm số
Câu 2: Vẽ đồ thị của hàm số. Hãy sử dụng đồ thị để biện luận theo tham số m, số điểm chung của parabol và
đường thẳng y = m.
Bài tập trắc nghiệm hàm số bậc hai
Câu 1: Cho parabol (P) có phương trình y = x^2 – 2x + 4 . Tìm điểm mà parabol đi qua.
A. M(- 3;19)
B. N(- 3;1)
C. P(4;0)
D. Q(4;2)
Câu 2: Cho parabol (P) có phương trình y = 3x^2 – 2x + 4 . Tìm trục đối xứng của parabol.
Câu 3: Cho parabol (P) có phương trình y = – x^2 – 2x + 4 . Tìm tọa độ đỉnh I của parabol.
A. I (- 1;5) .
B. I(1;1) .
C. I(- 1;1) .
D. I(- 2;4) .
Câu 4: Tìm tọa độ đỉnh của đồ thị hàm số y = x^2 – 2x + 3 .
A. I (1;2).
B. I (2;3).
C. I (- 1;6).
D. I (- 2;11).
Câu 5: Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây.
Câu 6: Tìm tọa độ giao điểm của đồ thị hàm số y = x^2 – 2019x + 2018 với trục tung.
A. Q (0;2018).
B. P(1;0).
C. (2018;0).
D. (1;2018).
Câu 7: Tìm giá trị M lớn nhất của hàm số y = – x^2 + 6x + 8 .
A. M=17.
B. M=8.
C. M=14.
D. M=48.
Câu 8: Tìm tọa độ giao điểm của đồ thị hàm số y = x^2 – 2018x + 2017 với trục hoành.
A. M(1;0) và N(2017;0) .
B. P(0;1) và Q(0;2017) .
C. O(0;0) và M(1;2017) .
D. N(2017;0) và O(0;0) .
Câu 9: Tìm hàm số bậc hai có đồ thị tiếp xúc với trục hoành.
A. y = 4x^2 + 4x + 1 .
B. y = – 4x^2 – 4x + 1.
C. y = x^2 + 4x – 4 .
D. y = x^2 + 4x + 7 .
Câu 10: Cho parabol (P) có phương trình y = 3x^2 – 6x + 2017 . Mệnh đề nào sau đây sai?
A. Parabol (P) có đỉnh I(0;2017) .
B. Parabol (P) không cắt trục hoành.
C. Parabol (P) luôn cắt trục tung.
D. Parabol (P) có trục đối xứng x = 1.
Câu 11: Đồ thị hàm số y = x^2 + bx + c là một parabol (P) có đỉnh I nằm trên trục tung đồng thời cắt trục hoành
tại hai điểm phân biệt A và B sao cho tam giác IAB có diện tích là 2căn2 . Tìm parabol (P).
A. 2 y = x – 2 .
B. 2 y = x + 2
C. 2 3 y = x – 2 .
D. 2 y = x – 4x + 1 .
Câu 12: Cho Parabol y = x² + x – 3 và đường thẳng y = 2x – 1. Khi đó
A. Parabol cắt đường thẳng tại hai điểm phân biệt
B. Parabol tiếp xúc với đường thẳng tại điểm (2; 3)
C. Parabol không cắt đường thẳng.
D. Parabol tiếp xúc với đường thẳng tại điểm (–1; –3)
Câu 13: Cho hàm số y = x^2 – 4x + 3, khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
B. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
C. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
Câu 14: Cho hàm số y = f (x) = 3x^4 + x^2 + 2 . Trong các mệnh đề sau, mệnh đề nào đúng?
A. y = f(x) là hàm số không có tính chẵn lẻ
B. y = f(x) là hàm số chẵn
C. y = f(x) là hàm số lẻ
D. y = f(x) là hàm số vừa chẵn vừa lẻ
Câu 15: Cho hàm số y = x^2 + 2x – 2. Khẳng định nào sau đúng?
A. Đồ thị của hàm số có đỉnh I (1;-4) .
B. Đồ thị hàm số có tung độ đỉnh I (-1;3).
C. Đồ thị hàm số có trục đối xứng: x = 1 .
D. Đồ thị hàm số có trục đối xứng: x = – 1 .
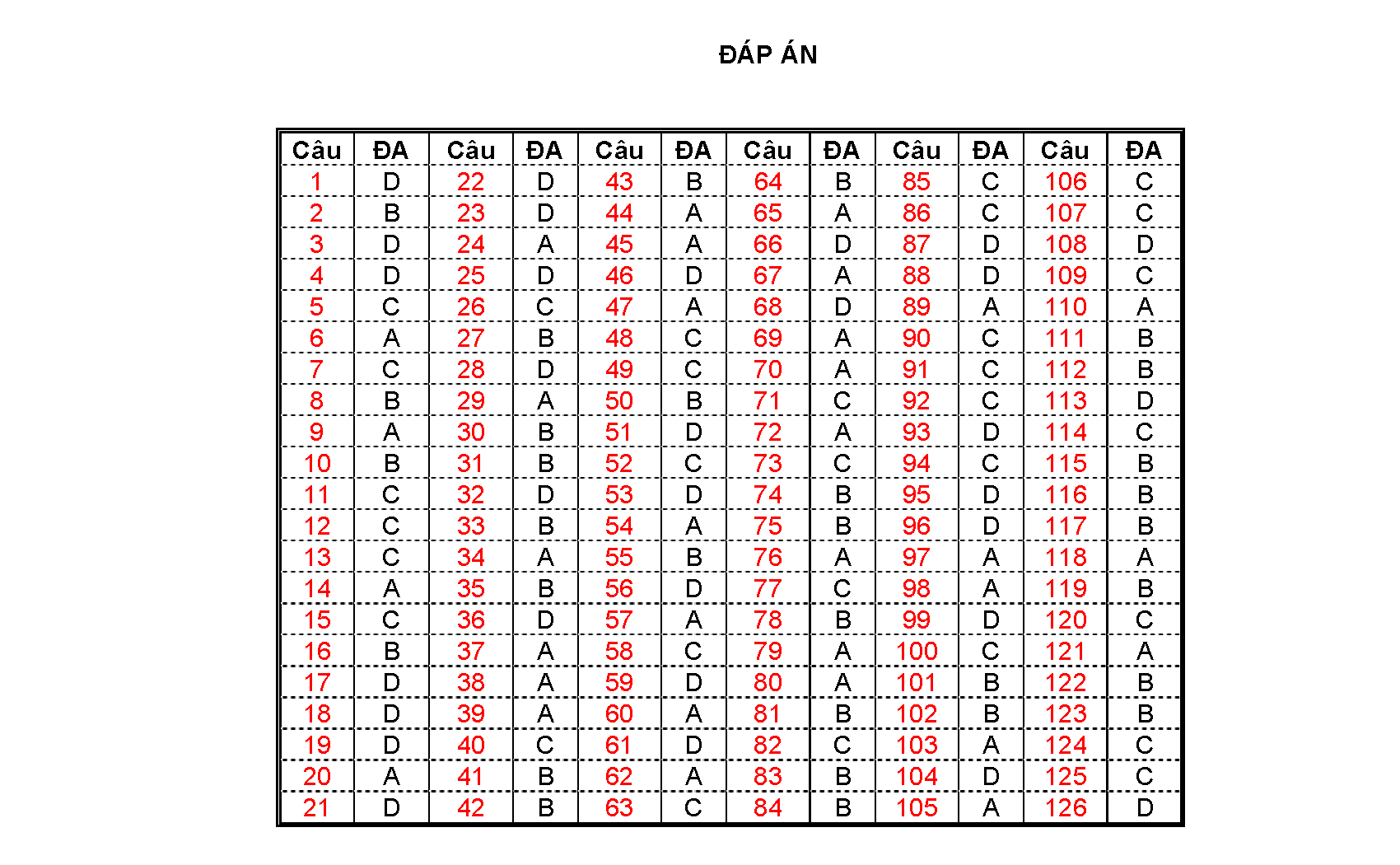
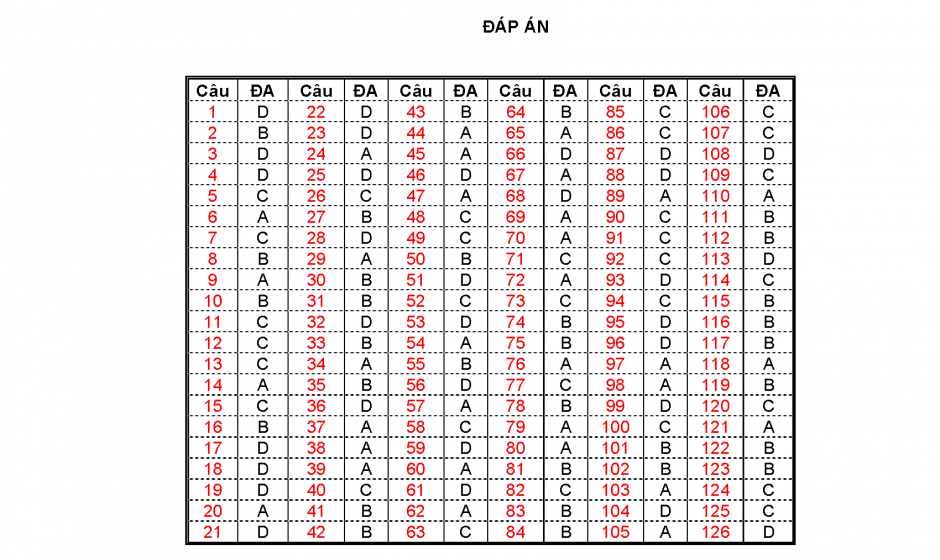
Đáp án trắc nghiệm
1 D 22 D 43 B 64 B 85 C 106 C
2 B 23 D 44 A 65 A 86 C 107 C
3 D 24 A 45 A 66 D 87 D 108 D
4 D 25 D 46 D 67 A 88 D 109 C
5 C 26 C 47 A 68 D 89 A 110 A
6 A 27 B 48 C 69 A 90 C 111 B
7 C 28 D 49 C 70 A 91 C 112 B
8 B 29 A 50 B 71 C 92 C 113 D
9 A 30 B 51 D 72 A 93 D 114 C
10 B 31 B 52 C 73 C 94 C 115 B
11 C 32 D 53 D 74 B 95 D 116 B
12 C 33 B 54 A 75 B 96 D 117 B
13 C 34 A 55 B 76 A 97 A 118 A
14 A 35 B 56 D 77 C 98 A 119 B
15 C 36 D 57 A 78 B 99 D 120 C
16 B 37 A 58 C 79 A 100 C 121 A
17 D 38 A 59 D 80 A 101 B 122 B
18 D 39 A 60 A 81 B 102 B 123 B
19 D 40 C 61 D 82 C 103 A 124 C
20 A 41 B 62 A 83 B 104 D 125 C
21 D 42 B 63 C 84 B 105 A 126 D
Qua tài liệu trên, mong rằng các bạn đã nắm vững hơn về phần kiến thức hàm số bậc hai lớp 10. Ngoài ra, tài liệu còn tổng hợp khá nhiều bài tập giúp các bạn có thể rèn luyện kiến thức một cách Logic nhất.
Tham khảo
1. https://vi.wikipedia.org/wiki/H%C3%A0m_s%E1%BB%91_b%E1%BA%ADc_hai
2. https://www.youtube.com/watch?v=X2SZm4bVMHU
Xem thêm video
video trên TOÁN THẦY TÙNG
( Phương pháp giải bài tập hàm số bậc hai lớp 10)
056.3753648
Chat FB