Tóm tắt tài liệu
Hệ phương trình đối xứng loại 2 là một dạng bài tập quan trọng trong chương trình toán học lớp 11 Đại số. Ở bài viết này, tailieure.com sẽ hướng dẫn cách nhận dạng và cách giải hệ phương trình đối xứng loại 2 cùng các bài toán có liên quan đến hệ phương trình đối xứng loại 2. Các em có thể tải tài liệu và in ra để tiện làm bài tập nhé. Chúc các em học tốt! Bạn đọc cũng có thể xem lại bài viết về hệ phương trình đối xứng loại 1
Lý thuyết về hệ phương trình đối xứng loại 2
Định nghĩa
Hệ phương trình đối xứng loại 2 là hệ phương trình có dạng: f(x;y) = a (*)
f(y;x) = a
Cách giải hệ phương trình đối xứng loại 2
Trừ hai phương trình của hệ cho nhau ta được: f(x; y)– f(y; x) = 0 ⇔ (x– y)g(x; y) = 0
Chú ý
- Nếu hệ phương trình ( ∗ ) có nghiệm x0 ; y0 thì y0 ; x0 cũng là nghiệm của hệ phương trình ( ∗ ). Từ đó suy ra, nếu hệ
phương trình ( ∗ ) có nghiệm duy nhất thì điều kiện cần là x0 = y0 - f(x; y) + f(y; x) = 2a là một phương trình đối xứng.
Ví dụ minh họa
Ví dụ 1
Giải các hệ phương trình sau.
1, x^3 + 1 = 2y
y^3 + 1 = 2x
Ví dụ 2
Giải các hệ phương trình sau.
1, 3/x^2 = 2x + y Điều kiện: x,y ≠ 0
3/y^2 = 2y + x
Ví dụ 3
Giải các hệ phương trình sau.
1, √x + √2– y = 2
√y + √2– x = 2
2, √5x + 1 + √12– y = 7 Điều kiện: 0 ≤ x, y ≤ 2.
√5y + 1 + √12– x = 7
Ví dụ 4
Giải các hệ phương trình sau.
1, x^3 = 2x + y
y^3 = 2y + x
2, (x – 1)(y^2 + 6) = y(x^2 + 1)
(y – 1)(x^2 + 6) = x(y^2 + 1)
Ví dụ 5
Tìm m để hệ phương trình sau có nghiệm: 2x + √y– 1 = m
2y + √x– 1 = m
Điều kiện: x, y ≥ 1.
Ví dụ 6
Tìm m để các hệ phương trình sau có nghiệm duy nhất:
1, x = y^2 – y + m.
y = x^2 – x + m.
2, 3x^2 = y^3 – 2y^2 + my.
3y^2 = x^3 – 2x^2 + mx.
1. Điều kiện cần: Giả sử hệ có nghiệm (x0; y0) thì (y0; x0) cũng là nghiệm của hệ nên để hệ có nghiệm duy nhất thì trước hết x0 = y0
Thay vào hệ ta được: x^2o – 2xo + m = 0, phương trình này có nghiệm duy nhất ⇔ Δ′ = 1– m = 0 ⇔ m = 1.
Điều kiện đủ: Với m = 1 hệ trở thành: x = y^2 – y + 1.
y = x^2 – x + 1.
Vậy hệ phương trình đã cho có nghiệm duy nhất khi và chỉ khi m = 1.
Ví dụ 7
Chứng minh rằng hệ phương trình 2x^2 = y + a^2/y có nghiệm duy nhất với mọi a ≠ 0.
2y^2 = x + a^2/x
Hệ phương trình ⇔2x^2 = y + a^2/y ⇒ 2xy(x – y) = y^2 – x^2 = (x -y)(2xy + x + y) = 0 ⇔ x = y (x,y>0 ⇒2xy+x+y>0)
2y^2 = x + a^2/x
Thay vào hệ phương trình, ta được: a^2 = 2x^3 – x^2 = f(x) ( ∗ ).
Xét hàm số: f(x) = 2x^3 – x^2 với x > 0
Ta có: f(x) = 2x(3x -1) ⇒ f′(x) = 0 ⇔ x =1/3
Mà f(0) = 0, f(1/3) = -1/27 và a^2 > 0 nên phương trình ( ∗ ) chỉ có duy nhất một nghiệm.
Vậy hệ đã cho luôn có nghiệm duy nhất với mọi a ≠ 0
Bài tập giải hệ phương trình đối xứng loại 2

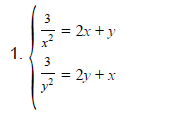
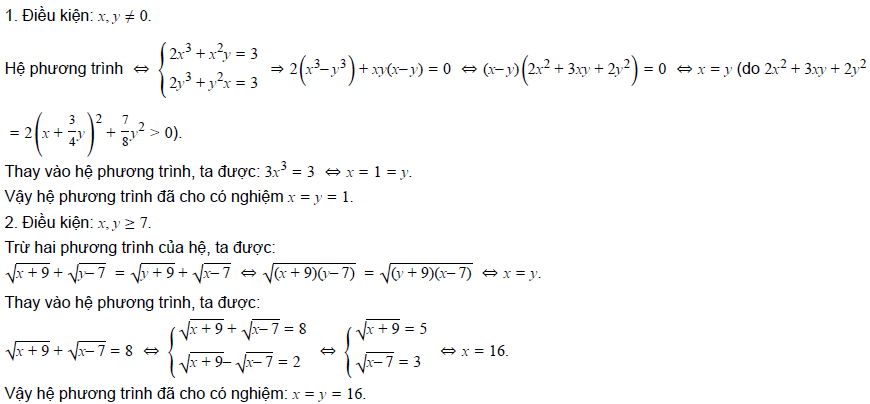

Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập về hệ phương trình đối xứng loại 2. Mong rằng với những bài toán bên trên có thể giúp các em một phần chinh phục chuyên đề này. Để đạt được kết quả cao nhất trong quá trình học chương về hệ phương trình, các em cần cẩn thận trong cách làm và phải làm nhiều dạng bài tập này. Cảm ơn các em đã đọc và tải tài liệu. Chúc các em học tốt!
Xem thêm: Các phương pháp giải hệ phương trình lớp 10




 056.3753648
056.3753648
 Chat FB
Chat FB