Tóm tắt tài liệu
Xét tính đúng sai của mệnh đề là một dạng bài tập thiết yếu nằm trong chương 1 phần Đại số lớp 10. Tài liệu dưới đây sẽ giúp các em hiểu rõ hơn về cách xét tính đúng sai của mệnh đề cũng như một số dạng bài tập đặc trưng nhất trong chuyên đề. Các em có thể tải tài liệu và in ra để tiện làm bài tập nhé.








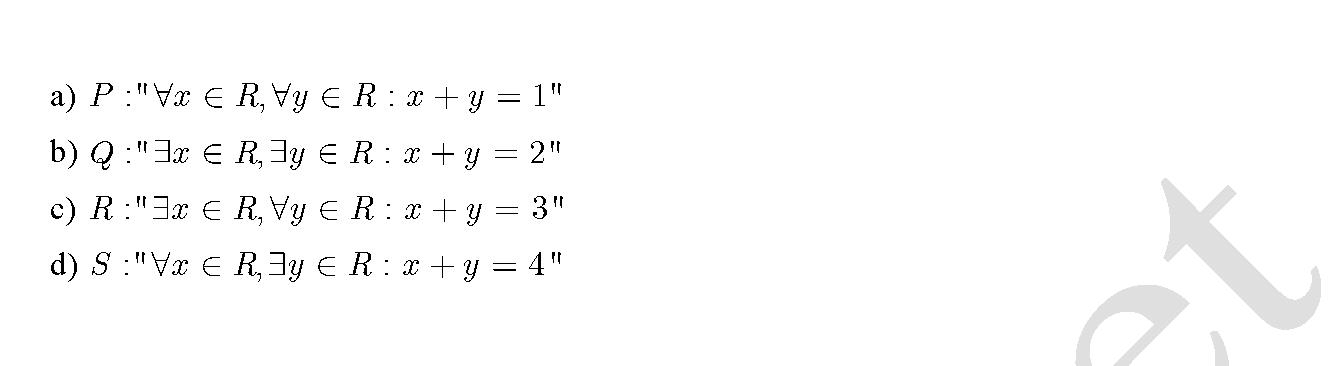
Dạng toán 1: Xác định mệnh đề và tính đúng sai của mệnh đề
Ví dụ 1: Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.
(1) Ở đây đẹp quá!
(2) Phương trình x^2 – 3x + 1 = 0 vô nghiệm.
(3) 16 không phải là số nguyên tố.
(4) Italia vô địch Worldcup 2006.
(5) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(6) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
Lời giải
Câu (1) không phải là mệnh đề (vì là câu cảm thán)
Các câu (3), (4), (6) là những mệnh đề đúng.
Câu (2), (5) là những mệnh đề sai.
Ví dụ 2: Cho ba mệnh đề sau, với n là số tự nhiên
(1) n + 8 là số chính phương
(2) Chữ số tận cùng của n là 4
(3) n – 1 là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai.
Lời giải
Ta có số chính phương có các chữ số tận cùng là 0, 1, 4, 5, 6, 9. Vì vậy
- Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn.
- Tương tự nhận thấy mệnh đề (2) và (3) cũng có mâu thuẫn.
Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Ví dụ 3: Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.
a) Không được đi lối này!
b) Bây giờ là mấy giờ?
c) Chiến tranh thế giới lần thứ hai kết thúc vào năm 1946.
d) 16 chia 3 dư 1.
e) 2003 không phải là số nguyên tố.
f) Hai đường tròn phân biệt có nhiều nhất là hai điểm chung.
Ví dụ 4: Tại Tiger Cup 98 có 4 đội lọt vào vòng bán kết: Vietnam, Singapore, Thailand và Indonesia. Trước khi thi đấu vòng bán kết, ba bạn Dung, Quang, Trung dự đoán như sau:
Dung: Singapore nhì, Thailand ba.
Quang: Vietnam nhì, Thailand tư.
Trung: Singapore nhất, Indonesia nhì.
Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy ?
Dạng toán 2: Các phép toán về mệnh đề
Lý thuyết
Các phép toán mệnh đề được sử dụng nhằm mục đích kết nối các mệnh đề lại với nhau tạo ra một mệnh đề mới. Một số các phép toán mệnh đề là: Mệnh đề phủ định (phép phủ định), Mệnh đề kéo theo (phép kéo theo), mệnh đề đảo, mệnh đề tương đương (phép tương đương).
Các ví dụ minh họa
Ví dụ 1: Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?
P :” Hình thoi có hai đường chéo vuông góc với nhau”
Q :” 6 là số nguyên tố”
R :” Tổng hai cạnh của một tam giác lớn hơn cạnh còn lại”
S :”5 3″
K :” Phương trình 4 2 x x2 2 0 có nghiệm “
Lời giải
Ta có các mệnh đề phủ định là
P :” Hai đường chéo của hình thoi không vuông góc với nhau”, mệnh đề này sai
Q :” 6 không phải là số nguyên tố”, mệnh đề này đúng
R :” Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại”, mệnh đề này sai
S : “5 3 “, mệnh đề này sai
K : “phương trình trên vô nghiệm”, mệnh đề này đúng.
Ví dụ 2: Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?
P: ”Trong tam giác tổng ba góc bằng 180 độ
Q: “2327 là số nguyên”
R: “Việt Nam vô địch Worldcup 2020”
K:” Bất phương trình 2013 x 2030 vô nghiệm “
Dạng toán 3: Mệnh đề chứa biến và mệnh đề chứa kí hiệu ∀, ∃
Ví dụ 1: Cho mệnh đề chứa biến “P x: x > x^3 ” , xét tính đúng sai của các mệnh đề sau:
a) P 1 b) P (1/3) c) ∀x N, P x d) ∃x N, P x
Lời giải
a) Ta có P 1 : 1 > 1^3 đây là mệnh đề sai.
b) Ta có P(1/3) : 1/3 > (1/3)^3 đây là mệnh đề đúng.
c) Ta có ∀x N, x > x^3 là mệnh đề sai vì P 1 là mệnh đề sai.
d) Ta có ∃x N, x > x^3 là mệnh đúng vì x – x^3 = x 1 – x 1+ x < hoặc = 0 ∀ số tự nhiên.
Ví dụ 2: Cho mệnh đề P : “Với mọi số thực x, nếu x là số hữu tỉ thì 2x là số hữu tỉ”.
Dùng kí hiệu viết P, P và xác định tính đúng – sai của nó.
b) Phát biểu MĐ đảo của P và chứng tỏ MĐ đó là đúng. Phát biểu MĐ dưới dang MĐ tương đương
Ví dụ 3: Cho số tự nhiên n. Xét hai mệnh đề chứa biến:
A(n) : “n l à số chẵn”, B(n) : “n2 là số chẵn”.
a) Hãy phát biểu mệnh đề A(n) B(n). Cho biết mệnh đề này đúng hay sai ?
b) Hãy phát biểu mệnh đề “ n , B(n) A(n) ”.
c) Hãy phát biểu mệnh đề “ n , A(n) B(n)”.
Ví dụ 4: Xét tính đúng sai của một số mệnh đề dưới đây..
Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập xét tính đúng sai của mệnh đề. Mong rằng với những bài toán trên sẽ giúp các em giải được những bài tập của chuyên đề này. Đây là một chuyên đề không quá khó nhưng nó tạo nền tảng cho các em giải các bài toán sau này. Do đó, cần phải nắm chắc kiến thức phần này. Cảm ơn các em đã xem và tải tài liệu.
Video giải bài tập
Tham khảo
1. https://www.youtube.com/watch?v=7UI5eGAhxpE
2. https://vi.wikipedia.org/wiki/M%E1%BB%87nh_%C4%91%E1%BB%81_to%C3%A1n_h%E1%BB%8Dc


 N, P x d) ∃x
N, P x d) ∃x 

 056.3753648
056.3753648
 Chat FB
Chat FB