Tóm tắt tài liệu
Trong quá trình học toán, không ít lần bạn nhận được câu hỏi từ bạn bên cạnh về các tập hợp số. Hôm nay TàiLiệuRẻ.com sẽ cùng tìm hiểu một tập khá quan trọng trong chương trình toán học. Đó là tập hợp z – tập hợp số nguyên. Bài viết này sẽ giúp các bạn hiểu hơn về tập hợp Z cũng như một số vấn đề liên quan.
TẢI XUỐNG↓
Định nghĩa tập hợp Z
Tập hợp Z hay còn gọi với các tên khác là số nguyên. Tập hợp số nguyên chỉ ra các số nguyên là miền xác định nguyên duy nhất mà các phần tử dương của nó được sắp thứ tự tốt và các thứ tự đó được bảo toàn dưới phép cộng. Tương tự như các tập hợp số khác, tập hợp Z cũng là một tập hợp vô hạn.
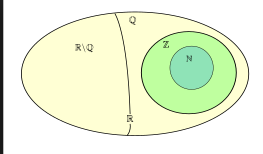
Ví dụ: -10; -9; -8; 100 ; 0
Tập hợp Z+ và Z-
Số nguyên được chia thành 2 trường phái là số nguyên dương và số nguyên âm. Sự phân chia này không chỉ có ý nghĩa về hình thức mà còn có ý nghĩa đại số vô cùng to lớn. Số nguyên dương được kí hiệu Z+, số nguyên âm kí hiệu là Z-. Đây là những kí hiệu không chính thống do mỗi quốc gia, mỗi nền giáo dục khác nhau qui định.
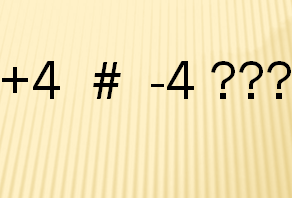
Ví dụ về tập hợp Z+: 1, 2, 3, 4, 5…
Ví dụ về tập hợp Z-: -10; -11; -8; -7…
Lưu ý rằng: Số 0 chẳng thuộc Z+ và cũng chẳng thuộc Z- mà là thuộc Z!
Định nghĩa về số nguyên và ví dụ
Tập hợp số nguyên chỉ ra các số nguyên là miền xác định nguyên duy nhất mà các phần tử dương của nó được sắp thứ tự tốt và các thứ tự đó được bảo toàn dưới phép cộng.
Tập hợp số nguyên là một tập vô hạn.
Các bài toán sử dụng tập hợp số nguyên
Trong toán học, các dạng bài tập về số nguyên thường rất đa dạng. Nhưng loại tập hợp này thường chỉ được ra điều kiện trong một bài toán khó. Hoặc ở các chương trình nhỏ hơn chẳng hạn toán lớp 6, số nguyên lại được sử dụng như một bài toán thực thụ:
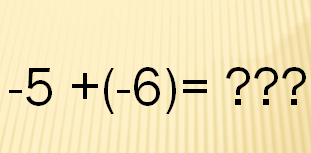
Tính hợp lý các biểu thức số nguyên sau
A = (-37) + 14 + 26 + 37
B= (-24) + 6 + 10 + 24
C = 15 + 23 + (-25) + (-23)
D = 60 + 33 + (-50) + (-33)
E = (-16) + (-209) + (-14) + 209
F = (-12) + (-13) + 36 + (-11)
G = -16 + 24 + 16 – 34
H = 25 + 37 – 48 – 25 – 37
I = 2575 + 37 – 2576 – 29
J = 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17
Vậy là chúng ta vừa tìm hiểu xong tập hợp Z hay còn gọi là tập hợp số nguyên. Nếu còn thắc mắc gì về tập hợp số trên, bạn đọc vui lòng để lại bình luận bên dưới bài viết. TàiLiệuRẻ.com nhất định sẽ giải đáp!
Câu hỏi về Tập hợp Z thường gặp
Tập hợp Z là gì ?
Tập hợp Z trong toán học ký hiệu cho tập hợp các số nguyên, bao gồm tất cả các số nguyên dương (1, 2, 3, ...), các số nguyên âm (-1, -2, -3, ...) và số 0. Ký hiệu Z bắt nguồn từ từ "Zahlen" trong tiếng Đức, có nghĩa là "số".
Cách biểu diễn của Tập hợp Z ?
Tập hợp Z được biểu diễn bằng ký hiệu Z và viết dưới dạng: {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Vị trí trên trục số:
- Số 0 nằm ở giữa.
- Các số nguyên dương nằm ở phía bên phải của 0.
- Các số nguyên âm nằm ở phía bên trái của 0.
Ví dụ:
- Các số -3, 0, 25 đều thuộc tập hợp Z.
- Các số như 1.3, 2/5, -3/6 thì không thuộc tập hợp Z, vì chúng không phải là số nguyên.
Z là tập hợp số gì lớp 6?
Trong chương trình Toán lớp 6, Z là ký hiệu của tập hợp các số nguyên, bao gồm các số nguyên dương (1, 2, 3,...), số nguyên âm (-1, -2, -3,...) và số 0. Tập hợp này được viết là {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Giải thích chi tiết:
- Số nguyên dương: Là các số tự nhiên khác 0, ví dụ: 1, 2, 3, ...
- Số nguyên âm: Là các số đối của các số nguyên dương, ví dụ: -1, -2, -3, ...
- Số 0: Là số trung tâm, nằm giữa các số nguyên dương và số nguyên âm.
Từ 1 đến 10 có bao nhiêu số nguyên tố?
Số nguyên tố nhỏ nhất và lớn nhất từ 1 đến 10 là bao nhiêu? Có tổng cộng 4 số nguyên tố từ 1 đến 10. Đó là 2, 3, 5 và 7. Trong danh sách này, 2 là số nguyên tố nhỏ nhất và 7 là số nguyên tố lớn nhất từ 1 đến 10.
R là tập hợp những số gì?
R là tập hợp các số thực, bao gồm tất cả các số có thể biểu diễn trên trục số, tức là bao gồm cả số hữu tỉ (như số tự nhiên, số nguyên, phân số) và số vô tỉ (như √2, π). Mỗi điểm trên trục số đều tương ứng với một số thực, và ngược lại.
Chi tiết về các loại số trong tập hợp R:
- Số tự nhiên (N): Bao gồm các số đếm 0, 1, 2, 3,...
- Số nguyên (Z): Bao gồm các số tự nhiên, số 0 và các số đối của chúng (ví dụ: ..., -3, -2, -1, 0, 1, 2, 3, ...).
- Số hữu tỉ (Q): Là các số có thể viết dưới dạng phân số a/b, với a và b là số nguyên và b khác 0.
- Số vô tỉ (I):Là các số không phải là số hữu tỉ, có biểu diễn thập phân vô hạn không tuần hoàn. Ví dụ điển hình là các số π và √2.
Xem thêm video
Tập hợp các số nguyên – Cô Nguyễn Diệu Linh (HAY NHẤT)
056.3753648
Chat FB