Lý thuyết hàm số bậc 2

Hàm số bậc 2 là một chủ đề thuộc chương II – Đại số lớp 10. Ở bài viết này Tài Liệu Rẻ sẽ tóm tắt lại tất cả kiến thức chuyên mục này. Để tìm hiểu về phần này, ta cần phải làm rõ các vấn đề: Định nghĩa hàm số bậc 2, đồ thị hàm số bậc 2.

Dưới đây là những tài liệu cần thiết để bạn có thể luyện tập để nắm chắc hơn mảng kiến thức này:

1. Định nghĩa hàm số bậc 2:

Hàm số bậc hai là hàm số có công thức: \[y=a{{x}^{2}}+bx+c(a\ne 0)\] có miền xác định \[D=R\].

2. Bảng biến thiên:

Bảng biến thiên đồ thị hàm số bậc 2

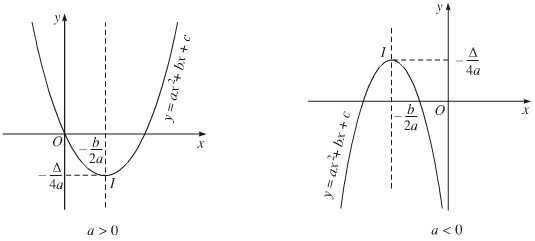
Đồ thị hàm số bậc 2

3. Đồ thị hàm số bậc 2:

Đồ thị hàm số \[y=a{{x}^{2}}+bx+c(a\ne 0)\] là đường thẳng parabol có: đỉnh \[I\left( \frac{-b}{2a};\frac{-\Delta }{4a} \right)\], trục đối xứng là đường thẳng \[x=\frac{-b}{2a}\].

Giao điểm với trục: \[A(0;c)\]. Hoành độ giao điểm với trục hoành là nghiệm của \[a{{x}^{2}}+bx+c=0\].

Đồ thị hàm số \[y=a{{x}^{2}}+bx+c(a\ne 0)\] suy ra từ đồ thị hàm số \[y=a{{x}^{2}}\] bằng cách:

+ Tịnh tiến song song với trục hoành \[\left| \frac{b}{2\text{a}} \right|\] đơn vị bên trái nếu \[\frac{b}{2\text{a}}\], về bên phải nếu \[\frac{b}{2\text{a}}\].

+ Tịnh tiến song song với trục tung \[\left| -\frac{\text{ }\!\!\Delta\!\!\text{ }}{4\text{a}} \right|\] đơn vị lên trên nếu \[-\frac{\text{ }\!\!\Delta\!\!\text{ }}{4\text{a}}\], và xuống dưới nếu \[-\frac{\text{ }\!\!\Delta\!\!\text{ }}{4\text{a}}\].

Vậy là chúng đã vừa tìm hiểu xong tất tần tật các khái niệm xoay quanh chương 2 hàm số lớp 10. Nếu có bất kì thắc mắc gì về phần kiến thức của chúng tôi tổng hợp, bạn có thể bình luận xuống dưới bằng cách đăng nhập bằng facebook để chúng tôi kịp thời sửa chữa.

• Chuyên mục: Hàm số bậc nhất và hàm số bậc hai