Tóm tắt tài liệu
Sau khi nắm vững khái niệm hàm số ở bài viết trước mà Win2888 uy tín đã giới thiệu. Bài viết này sẽ giúp các em hiểu rõ hơn về lý thuyết hàm số bậc nhất. Là một chuyên đề nền tảng khi các em đi sâu vào chương hàm số của đại số. Qua bài viết mong các em sẽ nắm bắt được hầu hết các kiến thức của chuyên đề hàm số cũng như phương pháp giải các loại bài tập này.
1. Định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số của một hay nhiều biến biểu diễn dưới dạng đa thức với bậc cao nhất của tất cả các biến là 1. Ví dụ với 3 biến \[x,y,z\] thì hàm số bậc nhất có dạng:
\[f(x,y,z)=ax+by+cz+d\]
Đối với trường hợp đặc biệt đơn biến thì hàm này có dạng:
\[f(x)=ax+b.\]
Và đây cũng là dạng các em sẽ tiếp xúc trong chương trình hàm số bậc nhất lớp 10: \[y=ax+b.\]
2. Sự biến thiên của hàm số
Hàm số bậc nhất \[y=ax+b(a\ne 0)\] có tập xác định \[D=\mathbb{R}\], đồng biến trên \[R\] nếu \[a>0\] và nghịch biến trên \[\mathbb{R}\] nếu \[a<0\].
Bảng biến thiên của hàm số bậc nhất tùy theo \[a\] như sau:
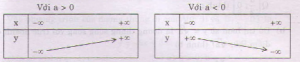
Sự biến thiên hàm số
3. Đồ thị hàm số bậc nhất
Đồ thị hàm số bận nhất \[y=ax+b(a\ne 0)\] là một đường thẳng không song song cũng không trùng với các trục tọa độ, cắt trục tung tại điểm \[P(0;b)\] và cắt trục hoành tại điểm \[Q=\left( \frac{-b}{a};0 \right)\]
Đồ thị hàm số bậc nhất
Ta gọi đồ thị của hàm số \[y=ax+b\] là đường thẳng \[ax+b\]. Số \[a\] gọi là hệ số góc của đường thẳng \[y=ax+b\].
4. Hàm số hằng (hàm hằng)
Kí hiệu: \[y=b\]
Khi \[a=0\] hàm số \[y=ax+b\] trở thành hàm hằng \[y=b\] là đường thẳng song song với trục hoành cắt trục tung tại điểm \[P(0;b)\]. Ta gọi đường thẳng này là đường thẳng \[y=b\].
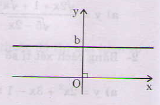
Đồ thị hàm hằng
5. Hàm số bậc nhất dưới dạng hàm trị tuyệt đối
Kí hiệu: \[y=|x|\]
\[y=|x|=x\] , Nếu x>0
\[y=|x|=-x\], Nếu x<0
Hàm số có tập xác định \[D=R\], đồng biến trên khoảng \[(0;+\infty )\] và nghịch biến trên khoảng \[(-\infty ;0)\].
Đồ thị là đường thẳng; trên nửa khoảng \[[0;+\infty )\] trùng với đồ thị hàm số \[y=x\] và trên khoảng \[(-\infty ;0)\] trùng với đồ thị hàm số \[y=-x\].
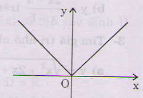
Đồ thị hàm số y=|x|
Các kiến thức do tailieure.com biên soạn một cách chi tiết rõ ràng và thống nhất. Bất cứ lỗi sai nào được phát hiện mong các em bình luận xuống phía cuối bài viết (đăng nhập để bình luận). Bài viết có sử dụng tài liệu tham khảo. Các em có thể xem thêm tại hướng dẫn đăng ký win2888.
Từ khóa bài viết:
