Tóm tắt tài liệu
Bất đẳng thức bunhiacopxki là một trong những bất đẳng thức khá dễ lầm lẫn. Thực chất mà nói đây chỉ là một nhánh nhỏ trong một bất đẳng thức lớn. Đó là: Bất đẳng thức Cauchy-Schwarz. Để tìm hiểu rõ bất đẳng thức này, chúng ta sẽ tìm hiểu thông qua các dạng công thức cơ bản ở dạng thông thường và dạng 2 – 3 – 4 bộ số. Tuy nhiên khi nắm vũng thì chỉ cần nhớ một dạng duy nhất, các dạng còn lại có thể tự suy luận tương ứng
Bất đẳng thức Bunhiacôpxki (BCS)
Cho 2 bộ số thực \[({{a}_{1}};{{a}_{2}};{{a}_{3}};…;{{a}_{n}})\] và \[({{b}_{1}};{{b}_{2}};{{b}_{3}};…;{{b}_{n}})\], mỗi bộ gồm n số. Khi đó ta có:
\[{{({{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+…+{{a}_{n}}{{b}_{n}})}^{2}}\le ({{a}_{1}}^{2}+{{a}_{2}}^{2}+{{a}_{3}}^{2}+…+{{a}_{n}}^{2})({{b}_{1}}^{2}+{{b}_{2}}^{2}+{{b}_{3}}^{2}+…+{{b}_{n}}^{2})\]
Dấu đẳng thức xảy ra khi và chỉ khi: \[\frac{{{a}_{1}}}{{{b}_{1}}}=\frac{{{a}_{2}}}{{{b}_{2}}}=…=\frac{{{a}_{n}}}{{{b}_{n}}}\] với quy ước nếu mẫu bằng 0 thì tử phải bằng 0.
Các hệ quả mở rộng
Hệ quả 1
Nếu \[{{a}_{1}}{{x}_{1}}+…+{{a}_{n}}.{{x}_{n}}=C\] (không đổi) thì \[\min (x_{1}^{2}+..+{{x}_{n}}^{2})=\frac{C}{a_{1}^{2}+…+a_{n}^{2}}\] đạt được khi \[\frac{{{x}_{1}}}{{{a}_{1}}}=\frac{{{x}_{2}}}{{{a}_{2}}}=…=\frac{{{x}_{n}}}{{{a}_{n}}}\]
Xem thêm: Bất đẳng thức tam giác
Kĩ thuật sử dụng bất đẳng thức bunhiacopxki


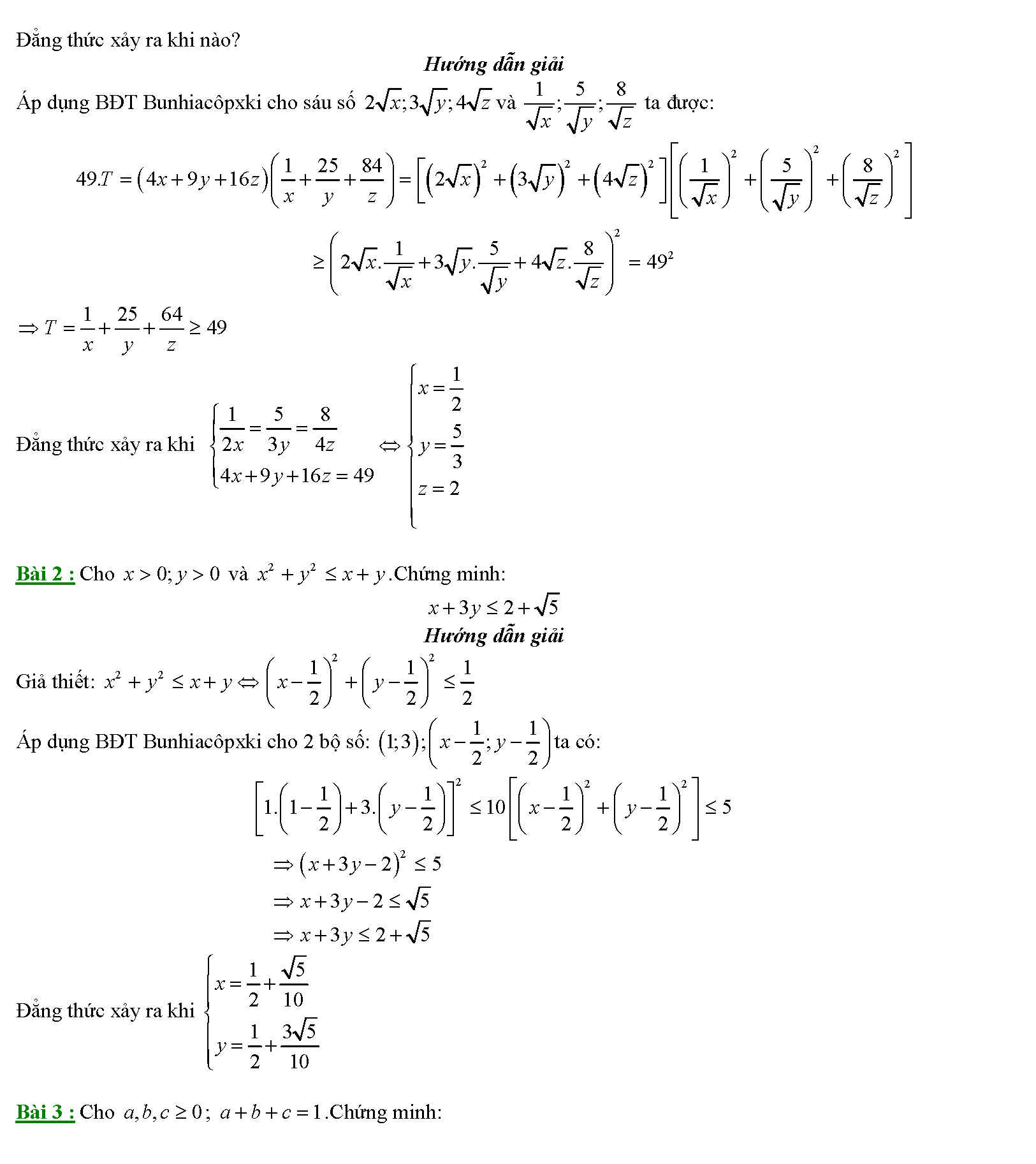
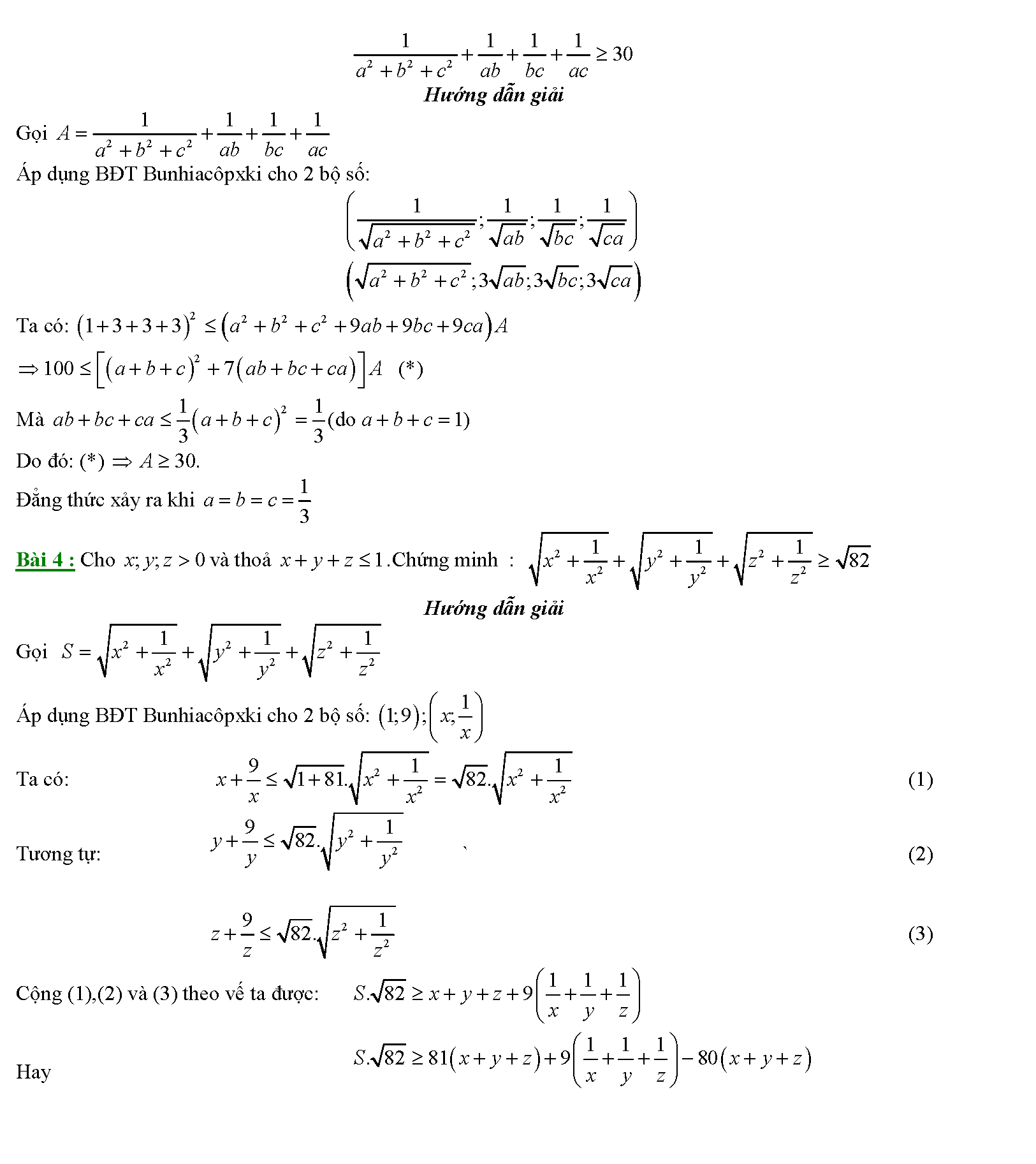



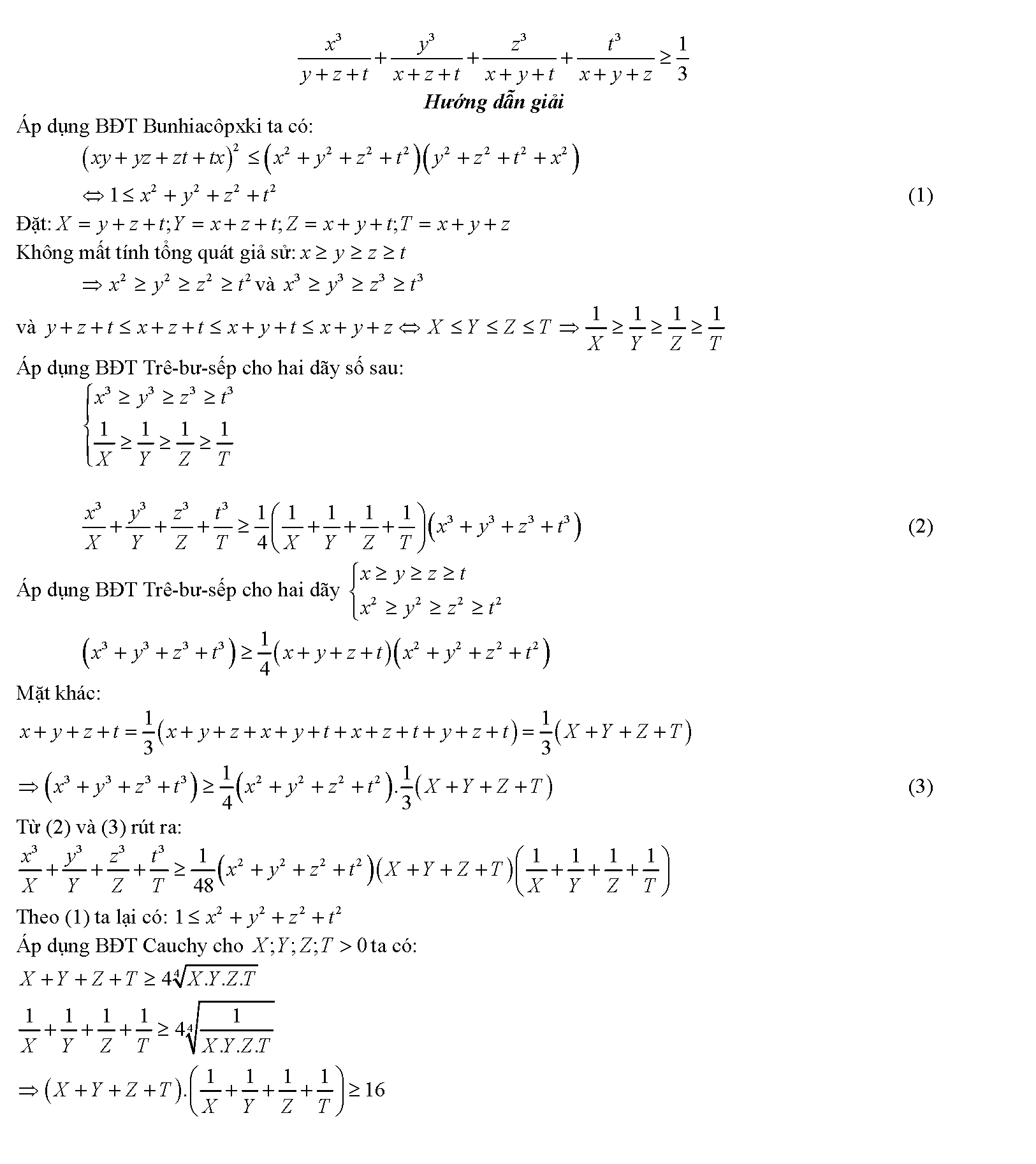
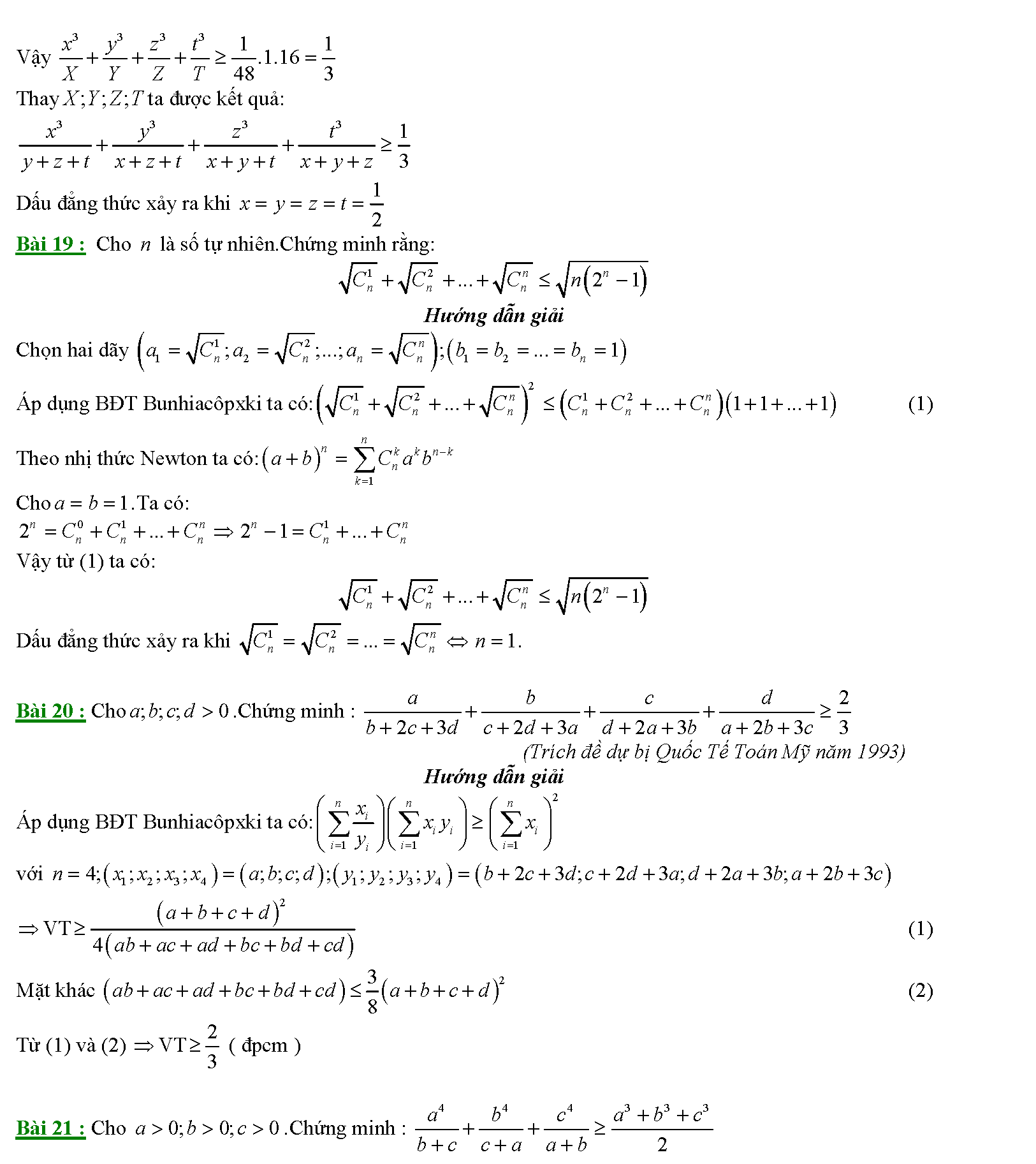

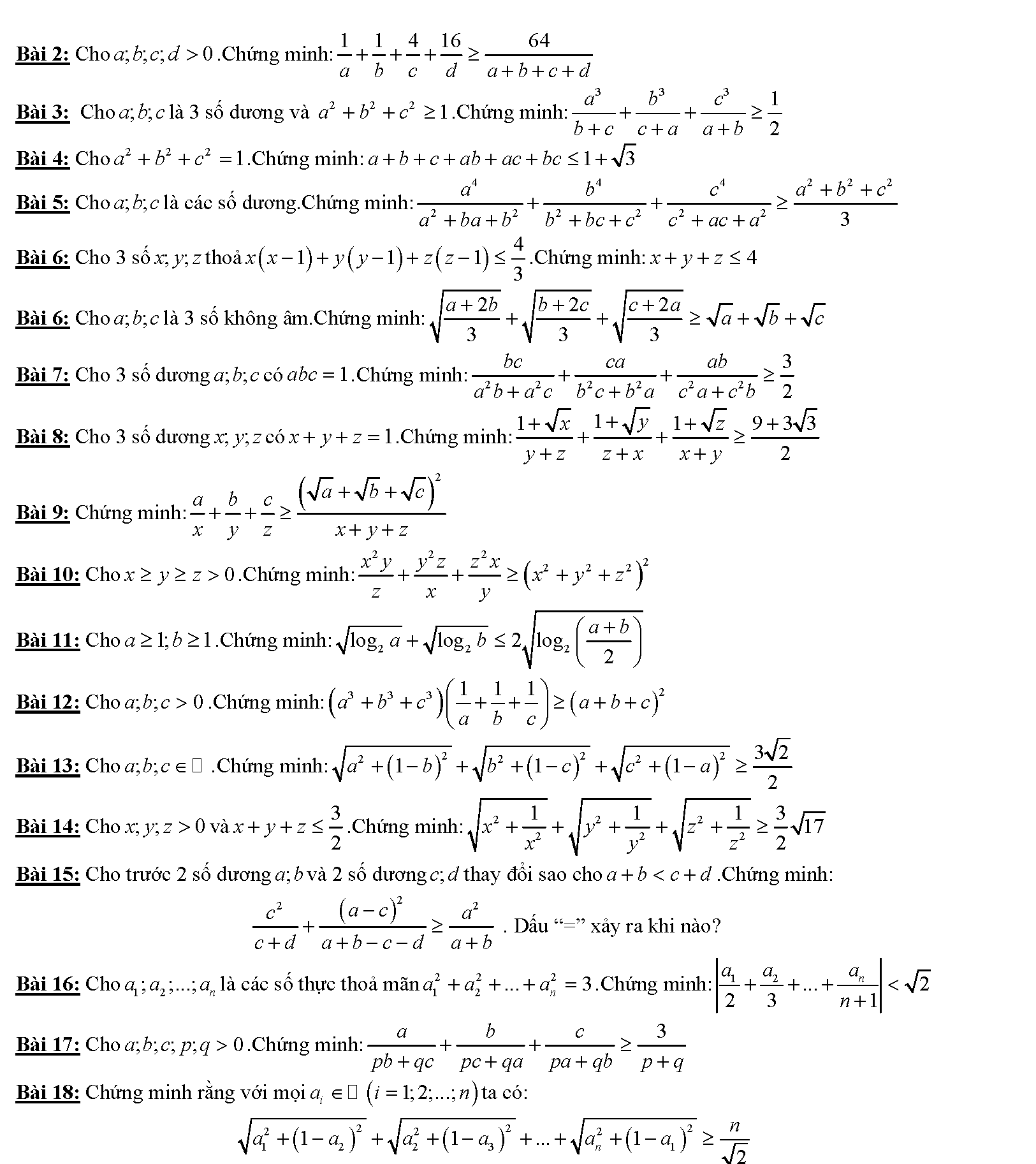















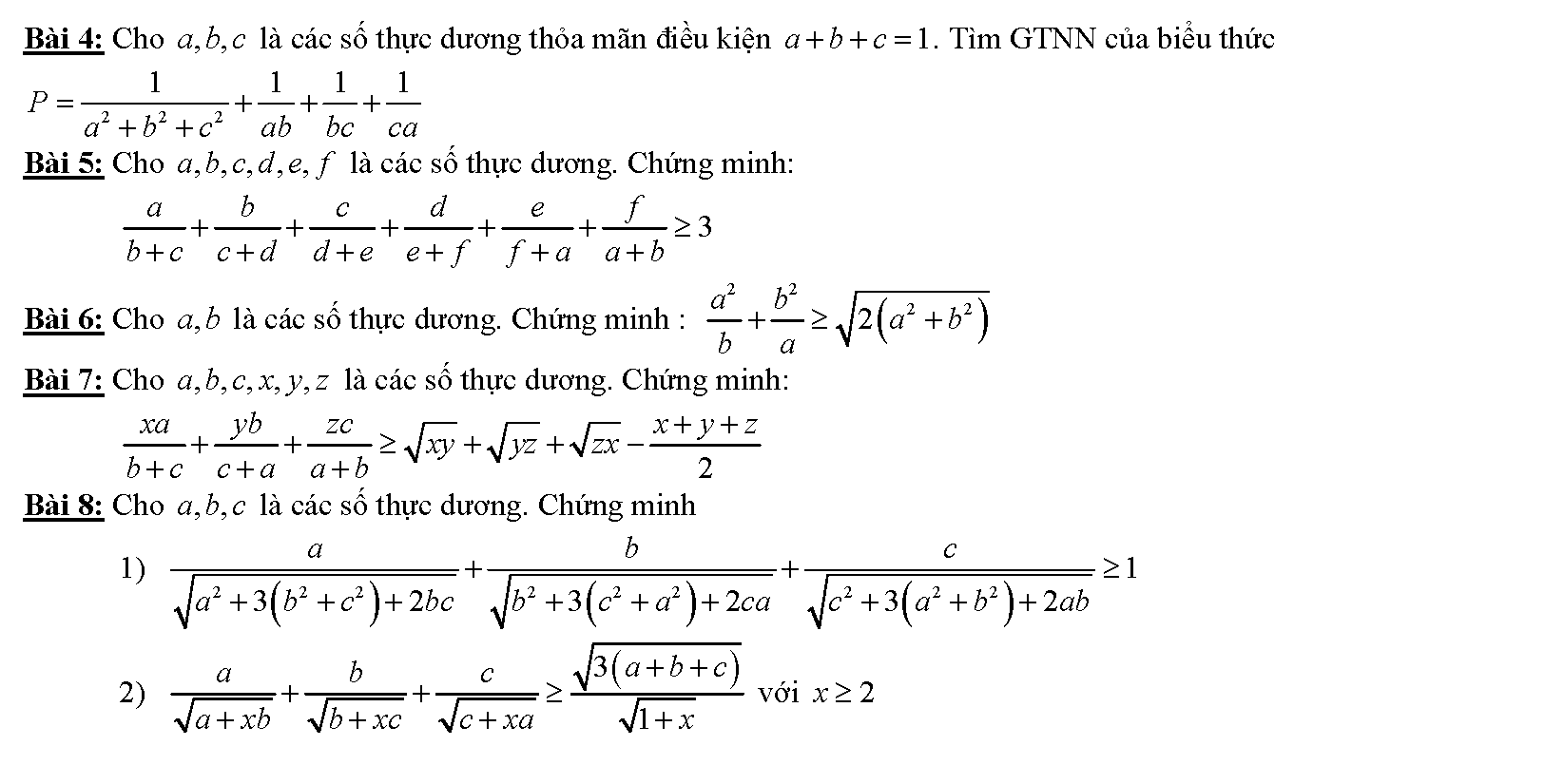
Vậy là chúng ta vừa tìm hiểu xong khá nhiều phương pháp cũng như bài tập liên quan đế bất đẳng thức bunhiacopxki. Để hiểu hơn về cách làm cũng như các phương pháp chứng minh bất đẳng thức khác, chúng ta cần phải thực hiện thật nhiều bài tập. Mỗi bài tập qua đó sẽ giúp hình thành tư duy, phản xạ liên kết. Giúp chúng ta thực hiện các dạng toán một cách dễ dàng hơn. Đặc biệt các bài toán trong các đề thi hsg có mức độ khó hơn rất nhiều thì tài liệu này lại có ý nghĩa hơn rất nhiều.
Xem thêm: Bất đẳng thức cosi



 056.3753648
056.3753648
 Chat FB
Chat FB