Tóm tắt tài liệu
Bất đẳng thức cosi hay còn gọi là bất đẳng thức trung bình cộng và trung bình nhân. Tên đúng chuẩn quốc tế của bất đẳng thức này là AM-GM. Có nhiều cách để chứng minh bất đẳng thức này nhưng hay nhất là cách chứng minh quy nạp của Cauchy. Vì vậy, nhiều người nhầm lẫn rằng Cauchy phát hiện ra bất đẳng thức này và đưa ra tên gọi đó. Tài liệu dưới đây cung cấp cho các bạn đầy đủ kiến thức cũng như những kỹ thuật để giải quyết bài tâp bất đẳng thức liên quan đến BĐT CÔ SI.
1. Công thức cô si
a) Dạng tổng quát:
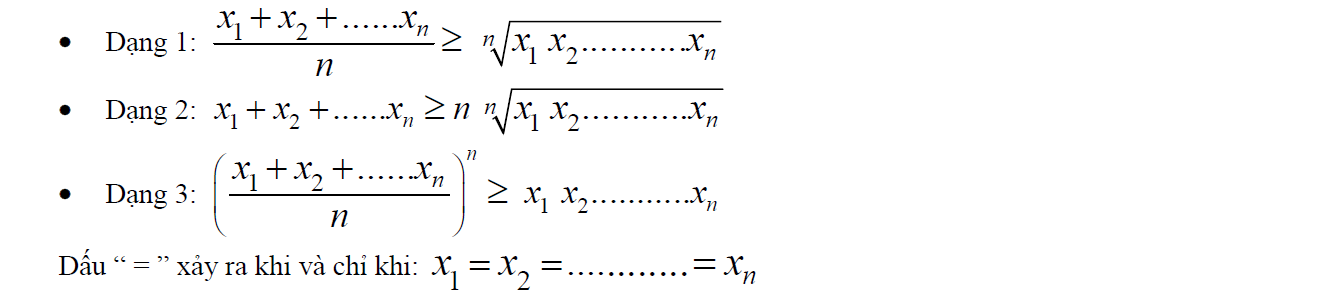b) Dạng cụ thể
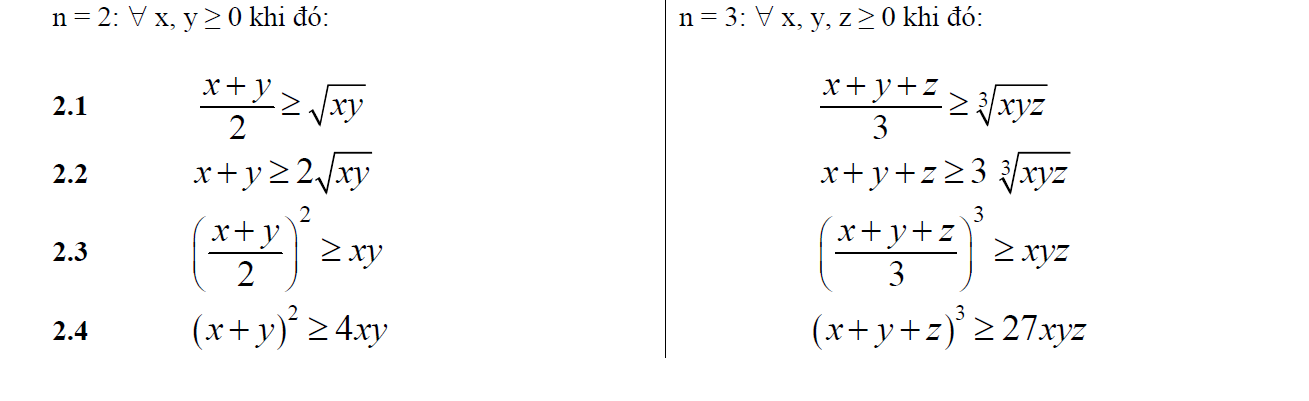
2. Kỹ thuật sử dụng bđt cô si
Để sử dụng thuần thục một bất đẳng thức cổ điển nào đó trong việc chứng minh các bất đẳng thức. Điều quan trọng nhất không phải là học thuộc lòng công thức và các tính chất của nó. Mà chính là ứng dụng các kĩ thuật riêng biệt của bất đẳng thức đó như thế nào cho hợp lí, logic. Dưới đây là một số kĩ thuật sử dụng bất đẳng thức cô si cực hay trong tài liệu, các em hãy cùng chú ý như sau:
- 2.1. Đánh giá từ trung bình cộng sang trung bình nhân
- 2.2. Kĩ thuật tách nghịch đảo
- 2.3. Kỹ thuật chọn điểm rơi
- 2.4. Đánh giá từ trung bình nhân sang trung bình cộng
- 2.5. Nhân thêm hằng số khi đánh giá TBN sang TBC
- 2.6. Ghép đối xứng
- 2.7. Kĩ thuật ghép cặp nghịch đảo cho 3 số, n số
- 2.8. Kỹ thuật đổi biến số
Xem thêm: Bất đẳng thức bunhiacopxki
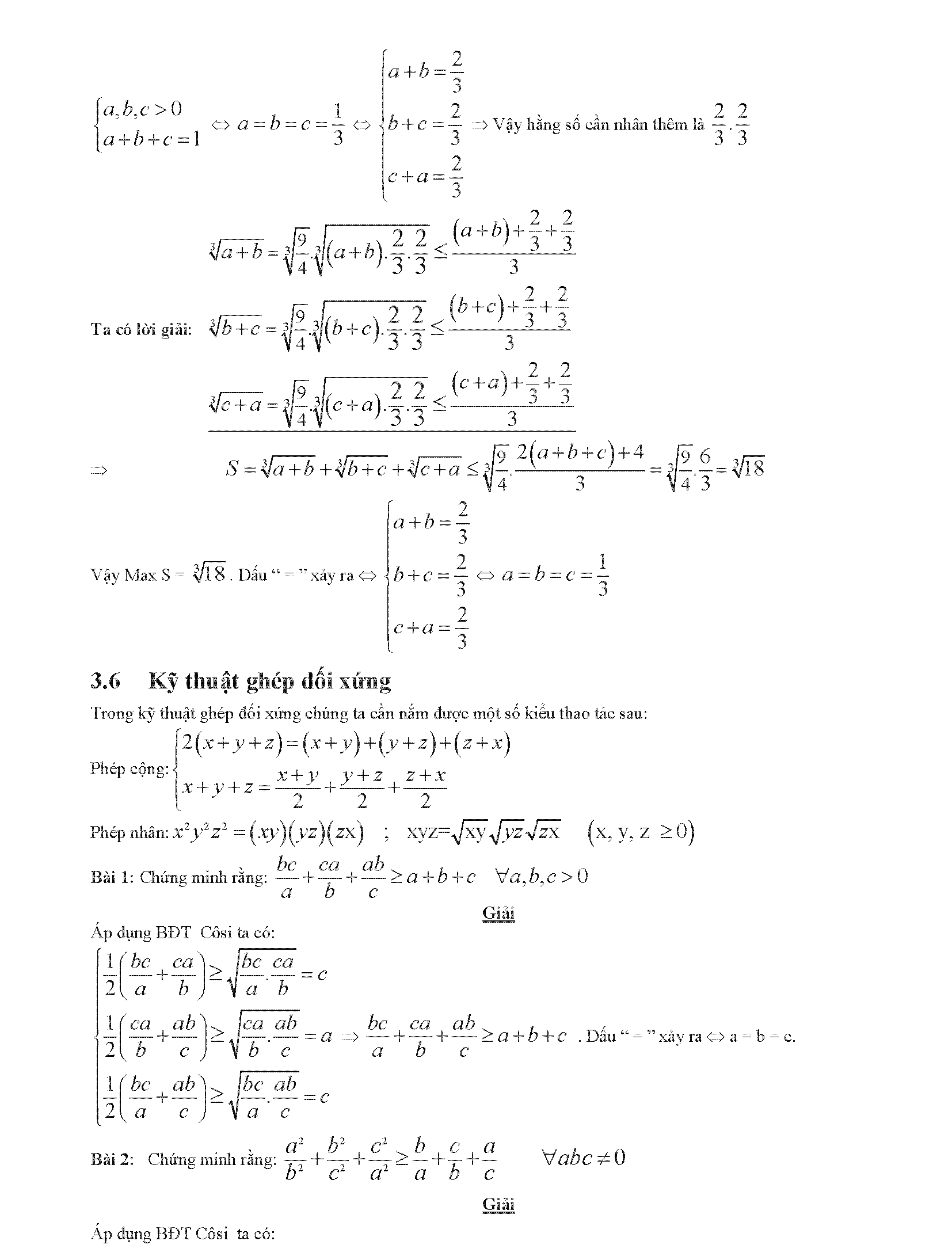
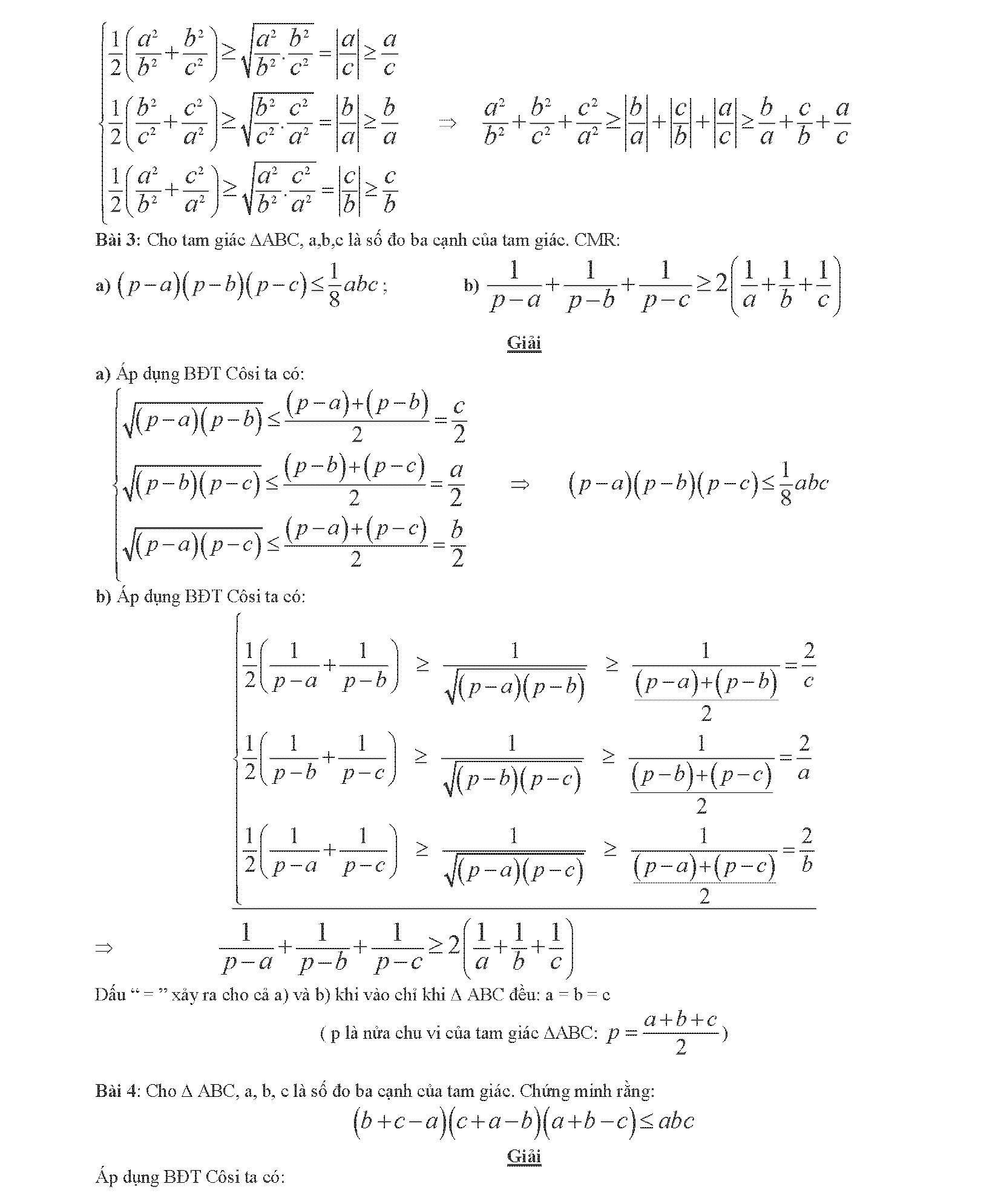
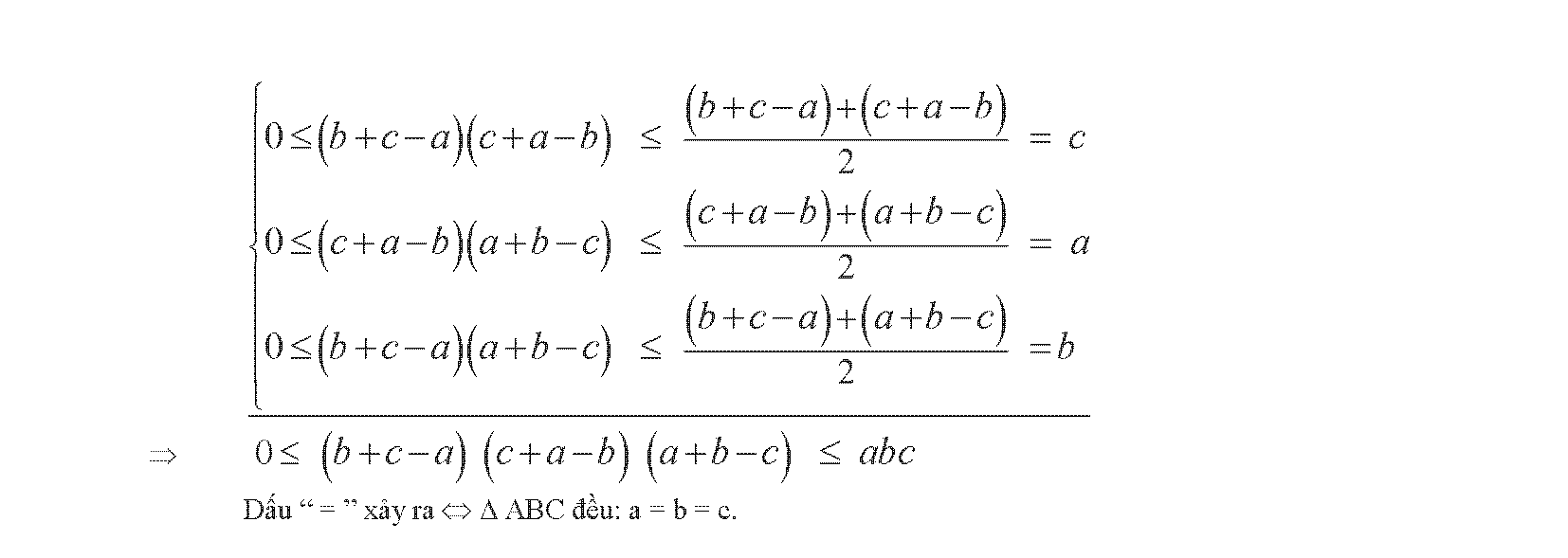
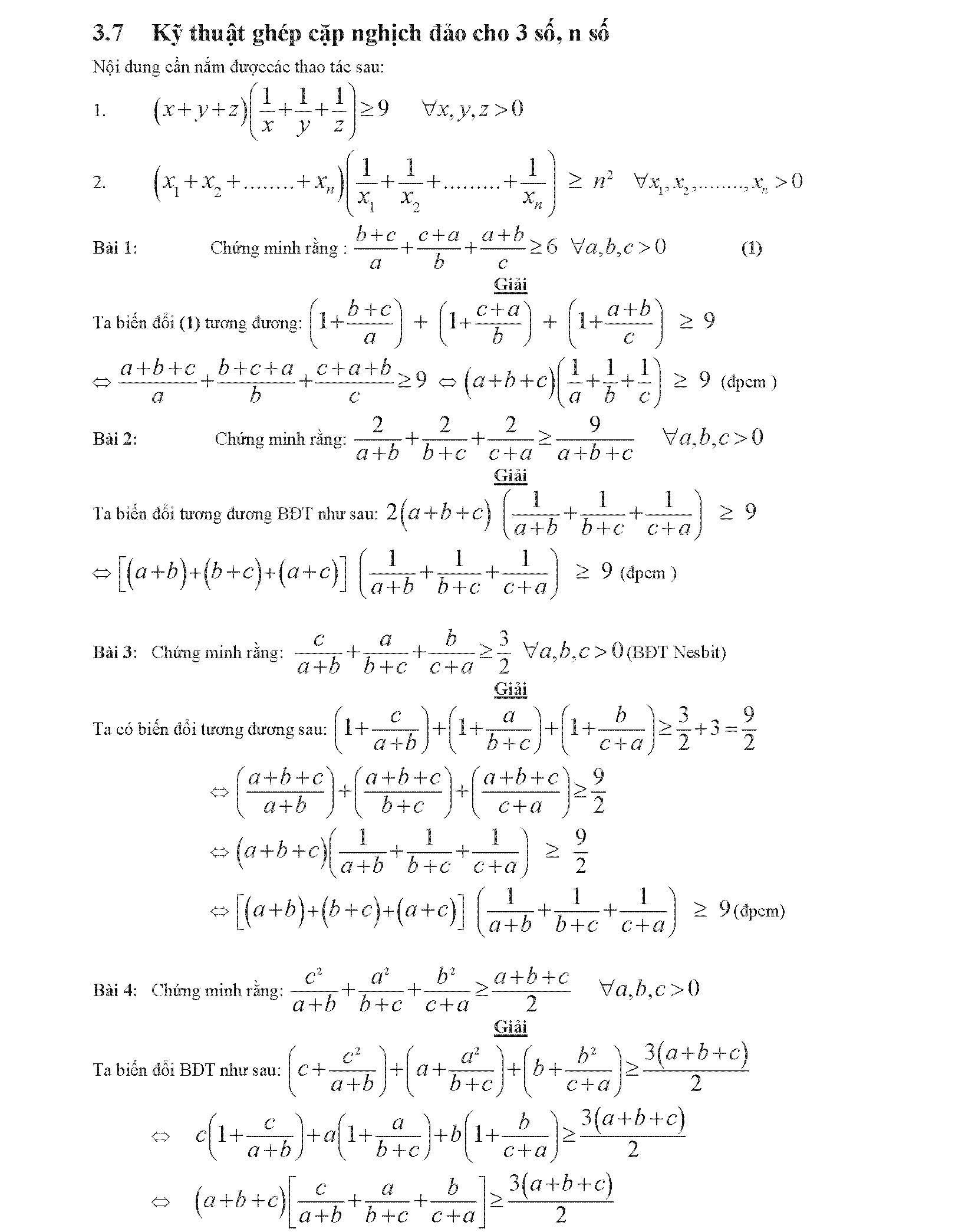
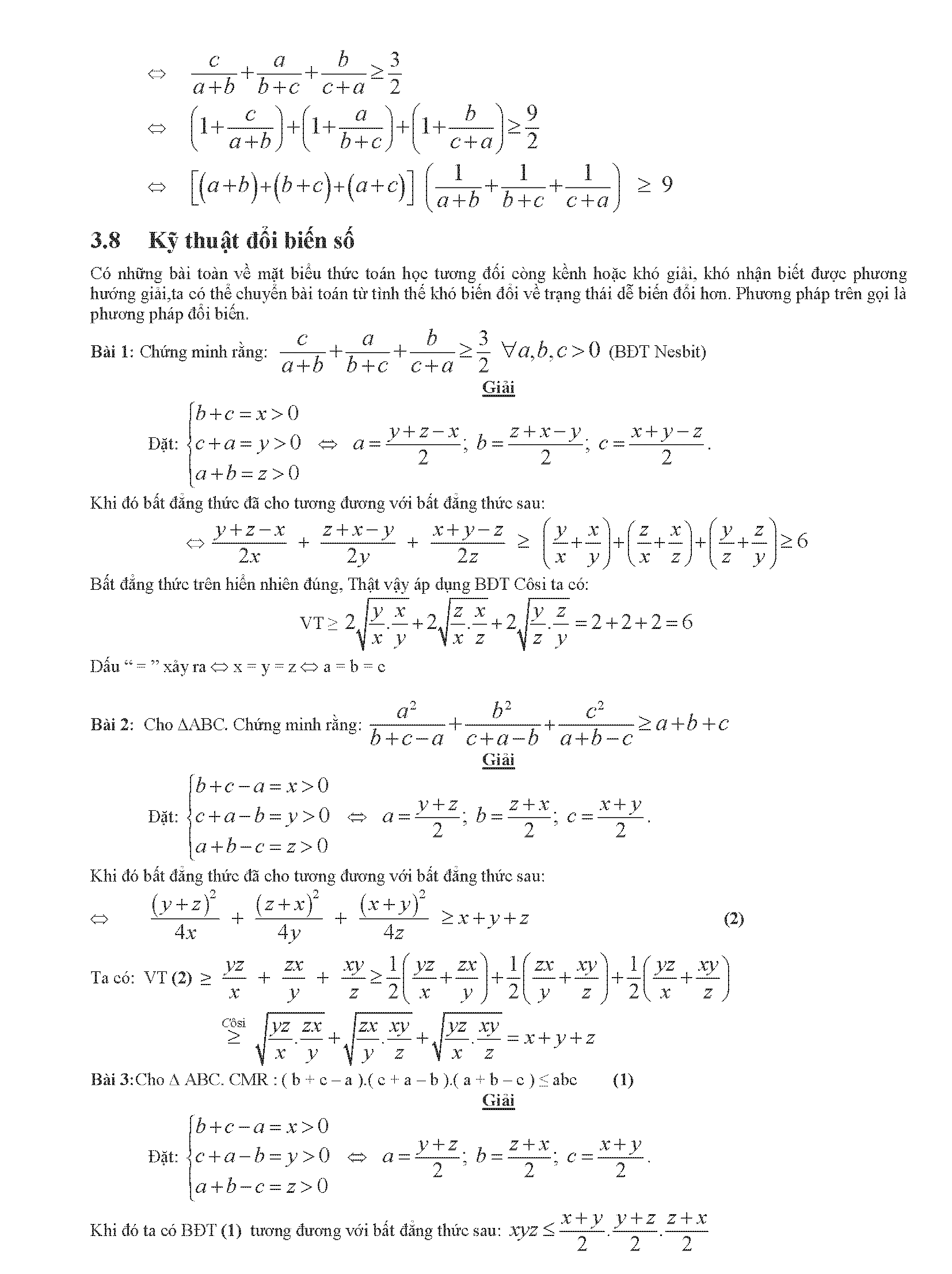
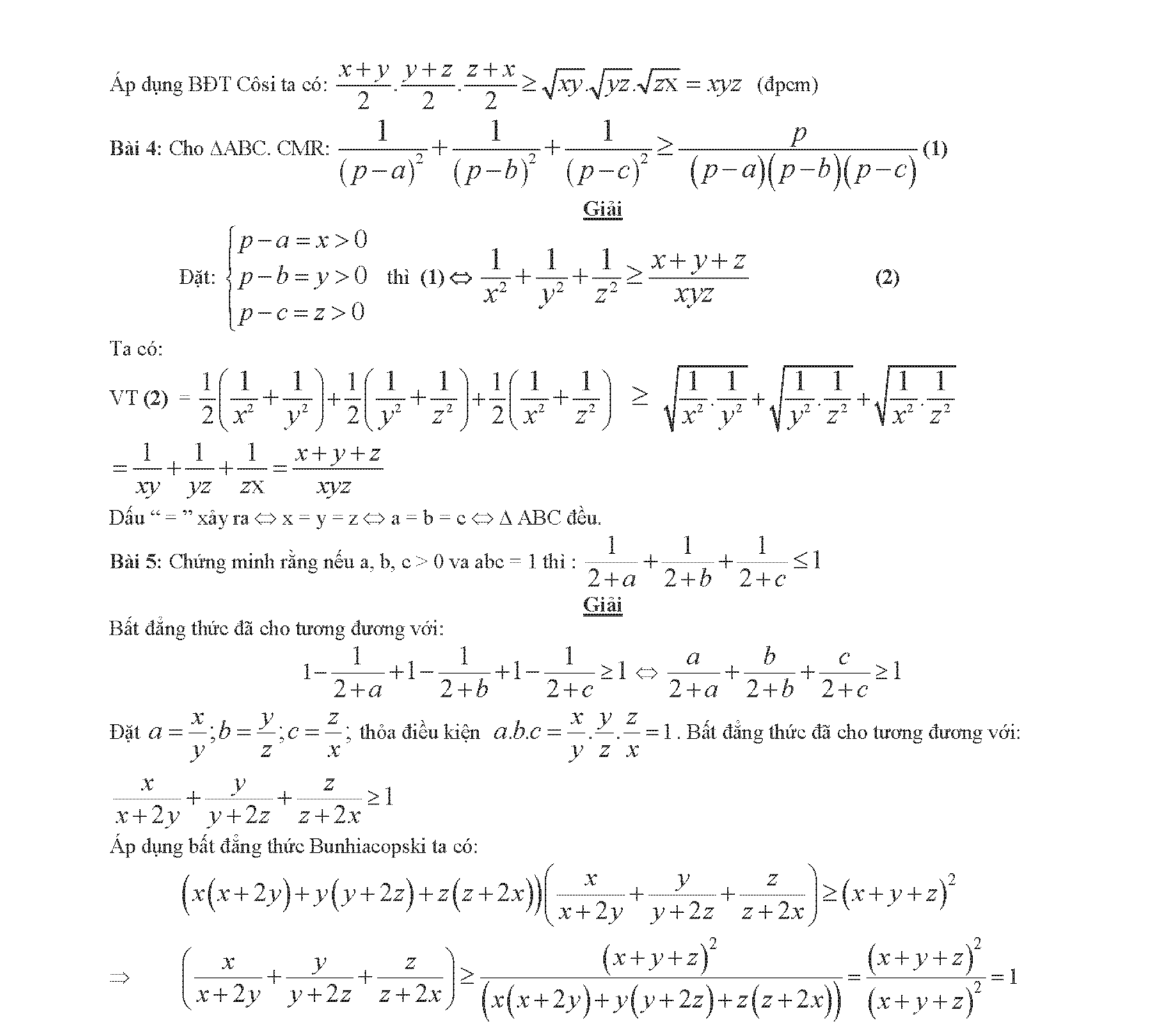
3. Ứng dụng bất đẳng thức cô si để giải phương trình và hệ phương trình
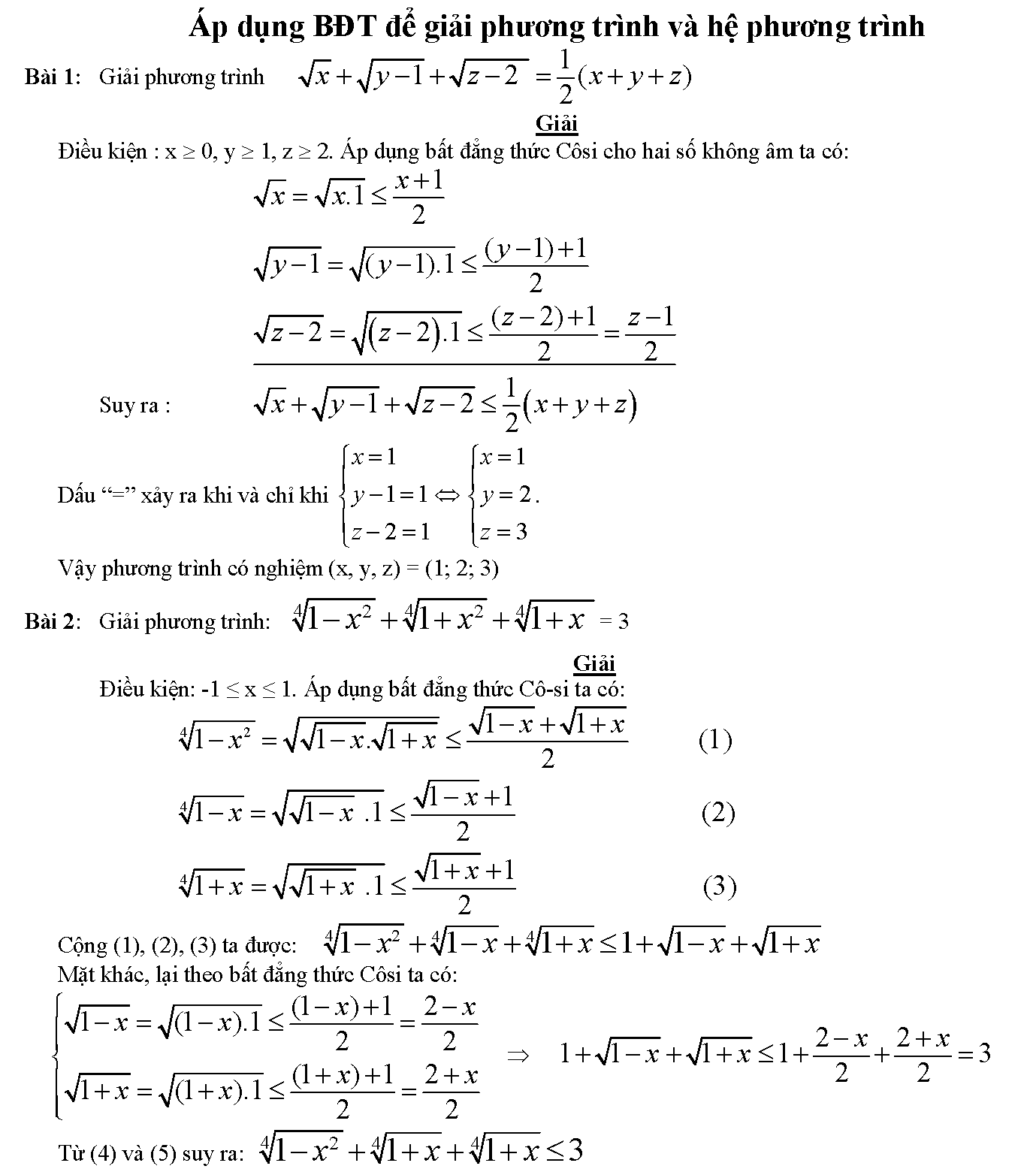
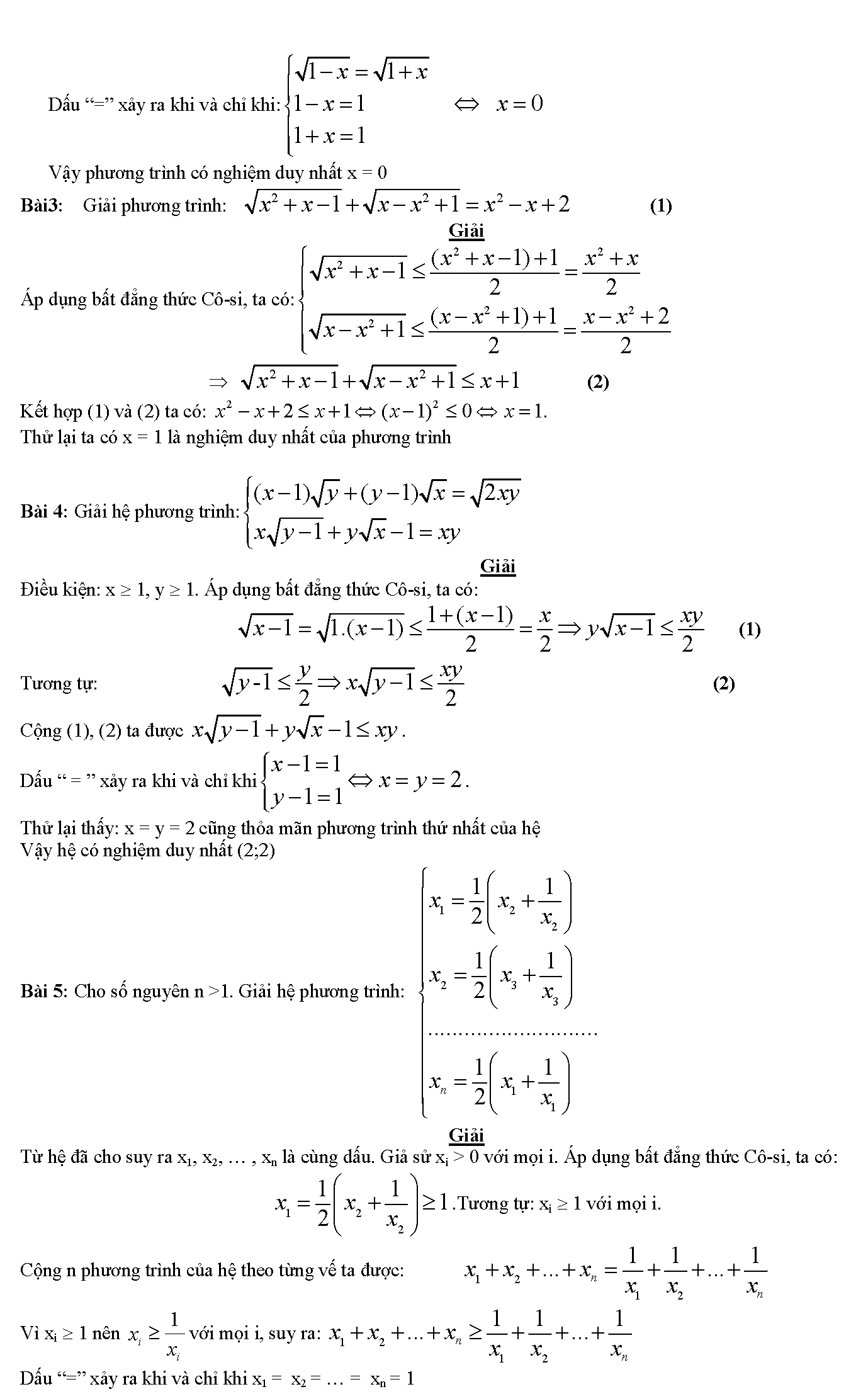
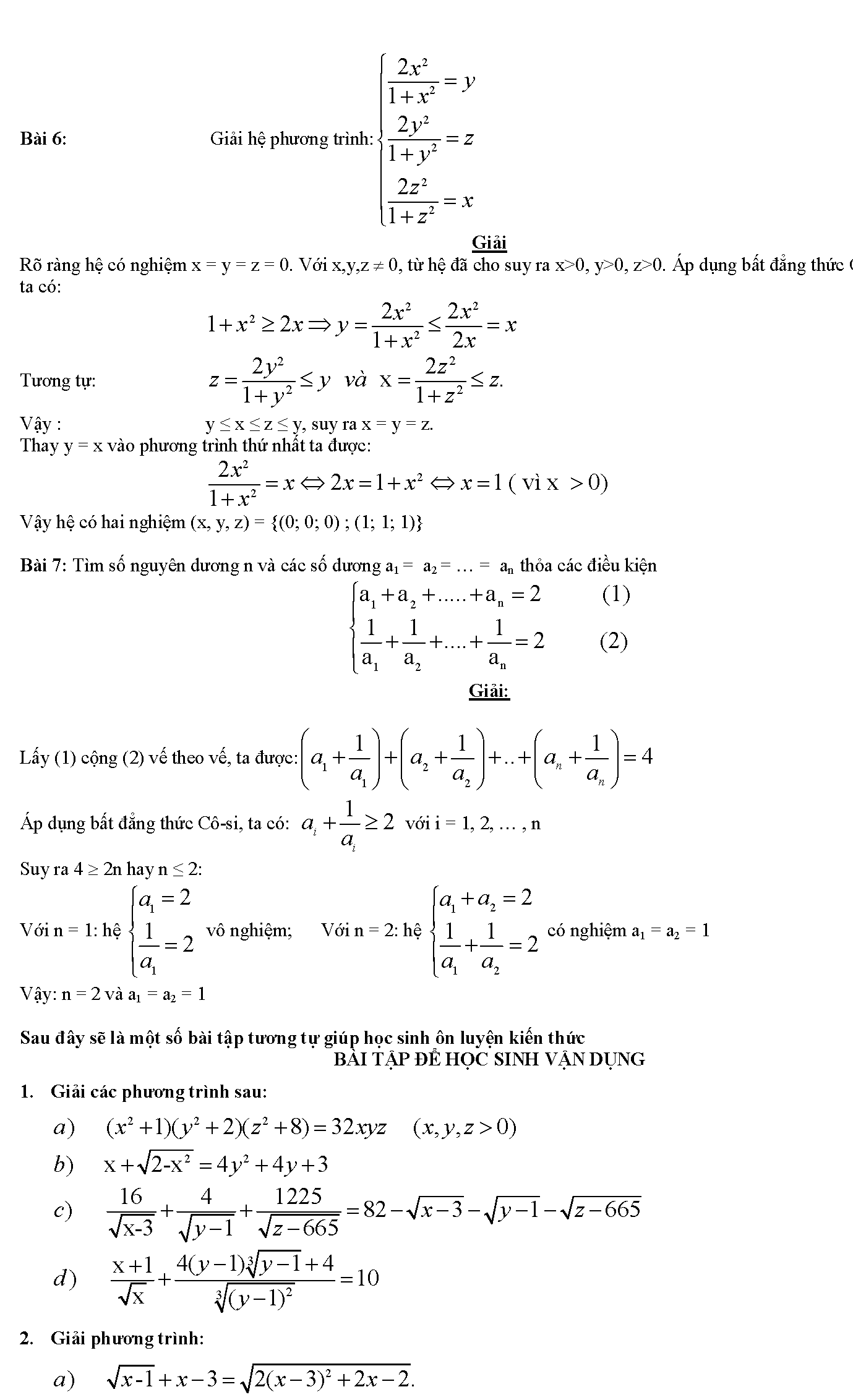
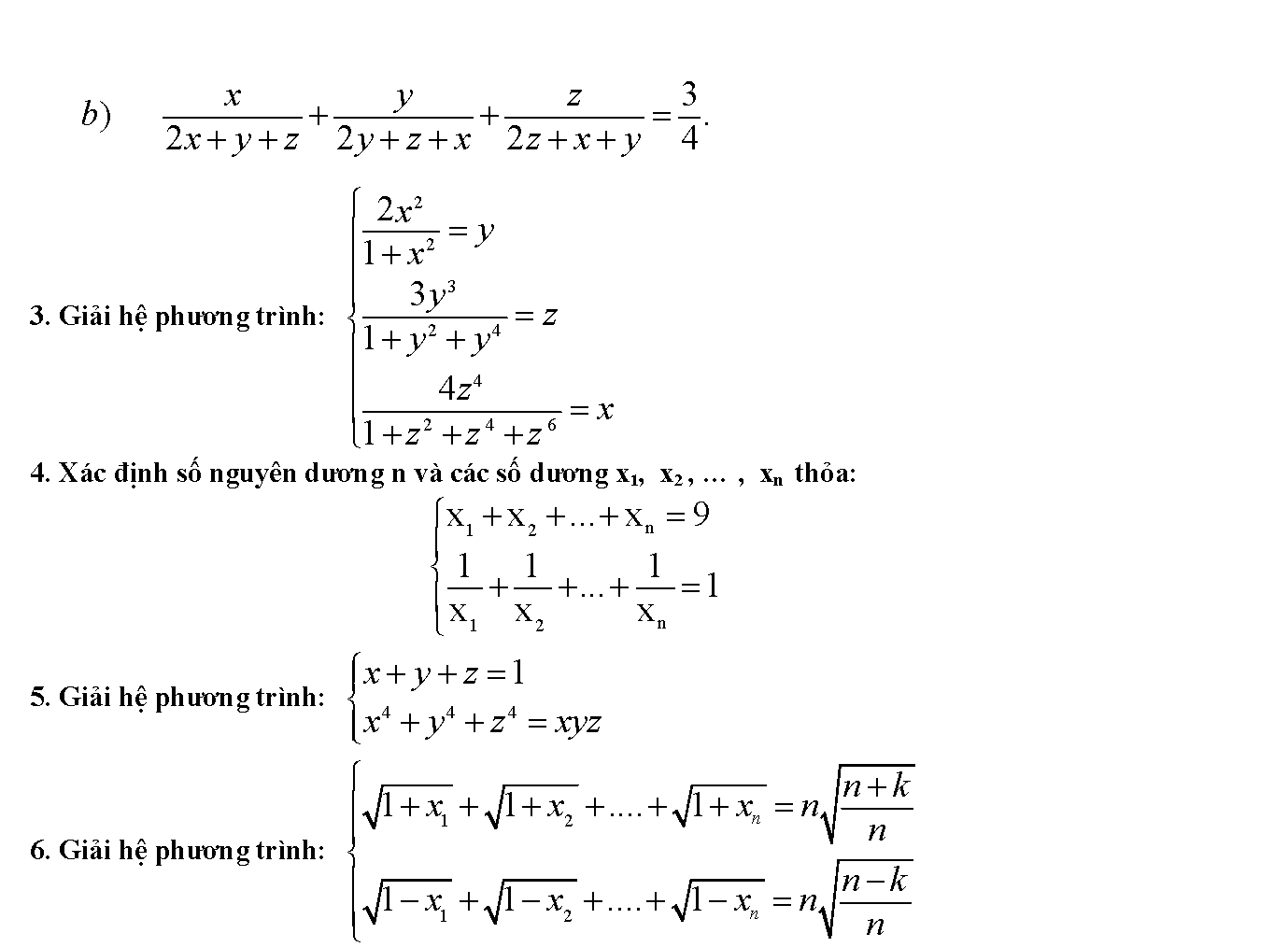
4. Bài tập bất đẳng thức cô si có lời giải
Bài 1: Chứng minh rằng \[({{a}^{2}}+{{b}^{2}})({{b}^{2}}+{{c}^{2}})({{c}^{2}}+{{a}^{2}})\ge 8{{a}^{2}}{{b}^{2}}{{c}^{2}},\forall a,b,c\]
Bài 2: Chứng minh rằng \[{{(\sqrt{a}+\sqrt{b})}^{8}}\ge 64ab{{(a+b)}^{2}},\forall a,b\ge 0\]
Bài 3: Chứng minh rằng \[(1+a+b)(a+b+ab)\ge 9ab,\forall a,b\ge 0\]
Bài 4: Chứng minh rằng \[3{{a}^{3}}+6{{b}^{3}}\ge 9a{{b}^{2}},\forall a,b\ge 0\]
Bài 5: Chứng minh rằng \[(a+b)(1+ab)\ge 4ab,\forall a,b\ge 0\]
Bài 6: Chứng minh rằng \[\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\]
Bài 7: Chứng minh rằng \[a+b+c\ge \sqrt{ab}+\sqrt{bc}+\sqrt{ca},\forall a,b,c\ge 0\]
Bài 8: Chứng minh rằng \[{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}\ge abc(a+b+c),\forall a,b,c\]
Bài 9: Chứng minh rằng \[(a+1)(b+1)(a+c)(b+c)\ge 16abc,\forall a,b,c\ge 0\]
Bài 10: Chứng minh rằng \[a+b+c\le \frac{1}{2}\left( {{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a+\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right),\forall a,b,c>0\]
Bài 11: Chứng minh rằng \[\frac{{{a}^{4}}}{b}+\frac{{{b}^{4}}}{c}+\frac{{{c}^{4}}}{a}\ge 3abc,\forall a,b,c>0\]
Bài 12: Chứng minh rằng \[a\left( \frac{a}{2}+\frac{1}{bc} \right)+b\left( \frac{b}{2}+\frac{1}{ca} \right)+c\left( \frac{c}{2}+\frac{1}{ab} \right)\ge \frac{9}{2},\forall a,b,c>0\]
Bài 13: Chứng minh rằng \[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}\ge {{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a,\forall a,b,c>0\]
Bài 14: Chứng minh rằng \[{{a}^{3}}{{b}^{3}}+{{b}^{3}}{{c}^{3}}+{{c}^{3}}{{a}^{3}}\ge abc\left( a{{b}^{2}}+b{{c}^{2}}+c{{a}^{2}} \right),\forall a,b,c>0\]
Bài 15: Chứng minh rằng \[\frac{{{a}^{3}}}{{{b}^{3}}}+\frac{{{b}^{3}}}{{{c}^{3}}}+\frac{{{c}^{3}}}{{{a}^{3}}}\ge \frac{{{a}^{2}}}{bc}+\frac{{{b}^{2}}}{ac}+\frac{{{c}^{2}}}{ab},\forall a,b,c>0\]
Bài 16: Chứng minh rằng \[\frac{{{a}^{5}}}{{{b}^{2}}}+\frac{{{b}^{5}}}{{{c}^{2}}}+\frac{{{c}^{5}}}{{{a}^{2}}}\ge {{a}^{3}}+{{b}^{3}}+{{c}^{3}},\forall a,b,c>0\]
Bài 17: Chứng minh rằng \[\frac{{{a}^{4}}}{{{b}^{2}}c}+\frac{{{b}^{4}}}{{{c}^{2}}a}+\frac{{{c}^{4}}}{{{a}^{2}}b}\ge a+b+c,\forall a,b,c>0\]
Bài 18: Chứng minh rằng \[\frac{{{a}^{5}}}{b{{c}^{2}}}+\frac{{{b}^{5}}}{c{{a}^{2}}}+\frac{{{c}^{5}}}{a{{b}^{2}}}\ge {{a}^{2}}+{{b}^{2}}+{{c}^{2}},\forall a,b,c>0\]
Bài 19: Chứng minh rằng \[\frac{{{a}^{4}}}{a+b}+\frac{{{b}^{4}}}{b+c}+\frac{{{c}^{4}}}{c+a}\ge \frac{a{{b}^{2}}+b{{c}^{2}}+c{{a}^{2}}}{2},\forall a,b,c>0\]
Bài 20: Chứng minh rằng \[\frac{{{a}^{6}}}{{{b}^{2}}c}+\frac{{{b}^{6}}}{{{c}^{2}}a}+\frac{{{c}^{6}}}{{{a}^{2}}b}\ge {{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a,\forall a,b,c>0\]
Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập và kĩ thuật liên quan đến bất đẳng thức cô si. Để đạt kết quả cao khi thực hành các dạng toán liên quan đến bất đẳng thức. Các em cần có một nền tảng kiến thức về biến đổi đại số vững chắc. Ngoài ra, việc ghi nhớ các bất đẳng thức cũng như những kĩ thuật sử dụng cũng là một yếu vô cùng quan trọng trên con đường chinh phục bất đẳng thức. Bất đẳng thức cô si là một bất đẳng thức khá dễ nhớ, tuy nhiên độ ảnh hưởng cũng như tầm quan trọng của nó là cực kì lớn. Do đó, các em học sinh có nguyện vọng thi học sinh giỏi thì không thể bỏ qua bất đẳng thức siêu kinh điển này.
Xem thêm: Bất đẳng thức vecto
Video học tập
Toán nâng cao lớp 8 – Bất đẳng thức Cauchy (Cô si) – Thầy Trần Tuấn Việt
056.3753648
Chat FB