Mệnh đề toán 10 là chương khởi động của chương trình toán trung học phổ thông. Qua bài viết này tailieure sẽ giúp bạn đọc tìm hiểu được thế nào là mệnh đề, mệnh đề được ứng dụng trong toán học như thế nào cũng như một số bài tập mệnh đề quan trọng.












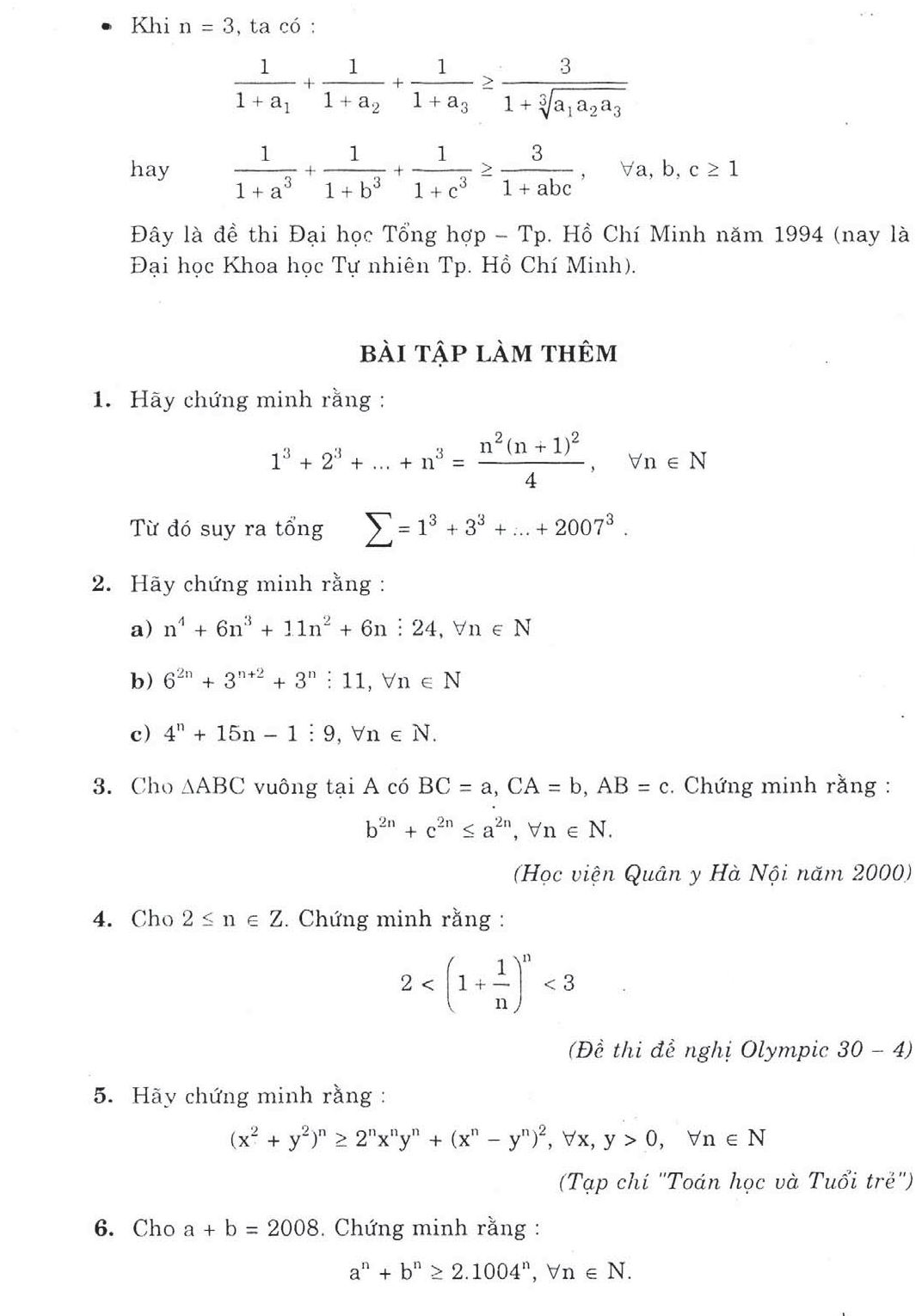




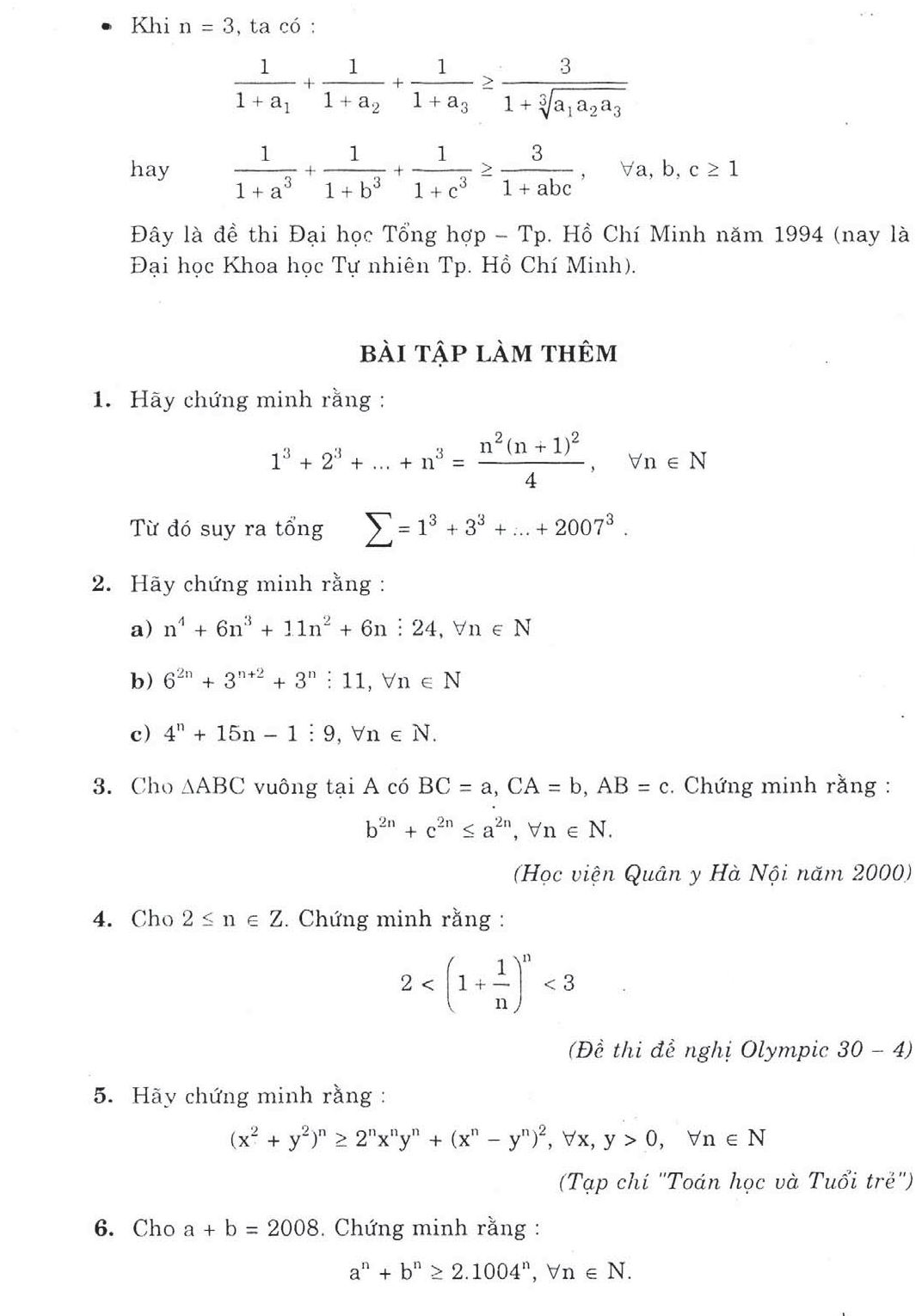
Kiến thức cơ bản mệnh đề
Lý thuyêt mệnh đề
Ở đây ta hiểu một mệnh đề là một phát biểu mà ta có thể gán cho nó một giá trị logic: Đúng hoặc sai.
Ví dụ:
1. ” Số 9 là số nguyên tố ” (Sai)
2. ” Thành phố Hồ Chí Minh không phải là Thủ Đô nước Việt Nam ” (đúng)
3. ” Maradona đã từng là cầu thủ bóng đá nổi tiếng nhất thê giới ” (đúng)
4. ” Nha Trang là một tỉnh của thành phố Ninh Thuận ” (Sai)
5. ” Một học sinh nếu học giỏi môn Toán thì sẽ học giỏi môn Vật Lí ” (Cái này chưa chắc chắn)
Kết luận: 1,2,3,4 là các mệnh đề còn 5 không phải là mệnh đề.
Các phép toán trên mệnh đề
1. Phép phủ định trong mệnh đề toán 10
Cho mệnh đề P. Khi đó ta gọi phủ đệnh của mệnh đề P là mệnh đề \[\overline{P,}\] (đọc là: không P), đúng nếu P sai, sai nếu như P đúng.
Ví dụ 1:
P: “10 chia hết cho 3” = > Mệnh đề phủ định của P là \[\overline{P,}\]: “10 không chia hết cho 3”
Ví dụ 2:
P: ” \[{{2005}^{2}}+{{2006}^{2}}\ge 2.2005.2006\] ” (mệnh đề đúng) => \[{{2005}^{2}}+{{2006}^{2}}<2.2005.2006\] là mệnh đề sai
2. Phép giao
Cho hai mệnh đề p và q. Khi đó ta gọi giao của hai mệnh đề p và q là mệnh đề mà đúng khi cả p và q và đúng và sai trong các trường hợp còn lại. Kí hiệu là: \[P\cap Q\]
Ví dụ: Giao của hai mệnh đề ” p > 2 ” và ” p <3 ” là: ” 2 < p < 3 ”
3. Phép hợp
Cho hai mệnh đề P và Q. Khi đó ta gọi hợp của hai mệnh đề P và Q là mệnh đề mà sai khi của P và Q đều sai và đúng trong các trường hợp còn lại. Kí hiệu \[P\cup Q\]
Ví dụ: Hợp của hai mệnh đề ” p > 2 ” và ” p = 2 ” là mệnh đề ” \[p\ge 2\] “.
4. Phép kéo theo
Cho hai mệnh đề P và Q. Khi đó ta gọi P kéo theo Q là mệnh đề sai nếu P đúng và Q sai và đúng trong các trường hợp còn lại. Kí hiệu là: \[P\Rightarrow Q\]
Nhận xét:
- Từ một mệnh đề sai ta luôn suy ra được mọi khẳng định đúng, vì vậy trong thực tế không bao giờ bàn luận về những vấn đề đã có giả thiết sai
- Thông thường ta có \[P\Rightarrow Q\], ta thường phát biểu là: Nếu P… thì Q…, trong đó P là điều kiện đủ để có Q và ngược lại Q là điều kiện cần để có P.
- Ví dụ: Nếu như \[a=b\] thì \[{{a}^{2008}}={{b}^{2008}}\]
5. Phép tương đương trong các mệnh đề
Cho hai mệnh đề P và Q. Khi đó ta gọi P tương đương Q là mệnh đề đúng khi P và Q cùng đúng hoặc cùng sai, sai trong các trường hợp còn lại. Kí hiệu: \[P\Leftrightarrow Q\]
Nhận xét: Thông thường ta đọc \[P\Leftrightarrow Q\] là: ” P là điều kiện cần và đủ để có Q ”
Ví dụ: \[”a=b\Leftrightarrow {{a}^{2007}}={{b}^{2007}}”\]
Các dạng toán về mệnh đề toán 10
Dạng 1: Dùng trực tiếp định nghĩa
Dạng toán này dựa trên các kiến thức sơ cấp về toán học để nhận biết đâu là mệnh đề đúng, đâu là mệnh đề sai.
Ví dụ 1: Nếu 12 > 25 thì nước sôi ở 100 độ C
Ví dụ 2: Nếu 3 < 4 thì 5 < 1
Ví dụ 3: Nếu 1 + 1 = 2 thì 1 + 3 = 5
Lời giải:
- Ví dụ 1: Mệnh đề đúng vì 12 > 15 là mệnh đề sai
- Ví dụ 2: Mệnh đề sai vì 3 < 4 đúng còn 5 < 1 thì sai
- Ví dụ 3: Mệnh đề sai vì 1 + 1 =2 là đúng còn 1 + 3 =5 là sai
Dạng 2: Dùng phép phản chứng
Để chứng minh một bài toán bằng phép phản chứng ta thực hiện như sau:
- Giả sử kết luận sai
- Ta chứng minh dẫn đến điều vô lí
- Kết luận điều phải chứng minh
Bài 1: Cho \[\left\{ \begin{matrix}a+b+c>0 \\ab+bc+ca>0 \\abc>0 \\\end{matrix} \right.\]. Chứng minh rằng \[a,b,c>0\]
Lời giải: Giả sử ngược lại, trong 3 số a,b,c có ít nhất một số \[\le 0\]. Vì a,b,c có vai trò như nhau, nên ta chỉ xem xét a \[\le 0\].
Khi đó: abc > 0 \[\Rightarrow a<0,bc<0\]
\[\Rightarrow a(b+c)=ab+ac>-bc>0\]
\[\Rightarrow a(b+c)=ab+ac>-bc>0\]
\[\Rightarrow a(b+c)>0\]
\[\Rightarrow b+c>0\] ( Vì chứng minh trên ta có a < 0)
\[\Rightarrow a+b+c<0\] ( vô lí)
Vậy ta kết luận: \[a,b,c>0\]
Bài 2: Chứng minh rằng nếu \[n\in N\] không phải là số chính phương thì \[\sqrt{n}\] là số vô tỉ
Dạng 3: Dùng phép qui nạp
Muốn chứng minh mệnh đề p(n) phụ thuộc vào n (\[n\in N\]) \[\forall n\ge {{n}_{0}}\]. Ta thực hiện 3 bước sau:
- Bước 1: \[n={{n}_{0}}\], Chứng minh p(no) đúng
- Bước 2: Giả sử \[n=k(k\in N,k\ge {{n}_{0}})\], chứng minh rằng p(n=k) đúng
- Bước 3: Giả sử \[n=k+1\], chứng minh p(k +1) đúng
Nguyên lí qui nạp cho phép chúng ta kết luận p(n) đúng \[\forall n\ge {{n}_{0}}\] đặc biệt khi no = 1 thì ta kết luận p(n) đúng với mọi n thuộc N.
Bài 1: Chứng minh rằng
\[{{1}^{2}}+{{2}^{2}}+…+{{n}^{2}}=\frac{n(n+1)(2n+1)}{6},\forall n\in N\]
Từ đó suy ra kết quả \[\sum ={{2}^{2}}+{{4}^{2}}+…+{{2004}^{2}}\]
Lời giải:
Với \[n=1\] ta có \[{{1}^{2}}=\frac{1.(1+2).(2.1+1)}{6}\] (đẳng thức này luôn đúng)
Giả sử \[n=k(k\in N)\] đẳng thức này đúng: \[{{1}^{2}}+{{2}^{2}}+…+{{k}^{2}}=\frac{k(k+1)(2k+1)}{6}\]
Ta chứng minh đẳng thức đúng với \[n=k+1\] tức \[{{1}^{2}}+{{2}^{2}}+…+{{k}^{2}}+{{(k+1)}^{2}}=\frac{k(k+1)(2k+1)}{6}+{{(k+1)}^{2}}\]
Ta có: \[{{1}^{2}}+{{2}^{2}}+…+{{k}^{2}}+{{(k+1)}^{2}}=\frac{k(k+1)(2k+1)}{6}+{{(k+1)}^{2}}\]
\[=\frac{1}{6}(k+1)\text{ }\!\![\!\!\text{ }k(2k+1)+6(k+1)\text{ }\!\!]\!\!\text{ }\]
\[=\frac{1}{6}(k+1).(\text{2}{{\text{k}}^{2}}+7k+6)\]
\[=\frac{(k+1)(k+2)(2k+3)}{6}\]
Theo nguyên lí qui nạp bài toán được chứng minh được như sau:
Áp dụng vào tính: \[\sum ={{2}^{2}}+{{4}^{2}}+…+{{2004}^{2}}={{2}^{2}}.({{1}^{2}}+{{2}^{2}}+…+{{1002}^{2}})=4.\frac{1002.(1002+1).(2004+1)}{6}=1343358020\]
Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập và kiến thức xoay quanh chuyên đề mệnh đề toán 10. Có lẽ giờ các bạn đã có thể hiểu hơn về chương khởi động này của chương trình đại số THPT. Nếu còn thắc mắc gì về bất cứ mảng kiến thức nào trong chuyên đề, các bạn có thể để lại câu hỏi xuống phía bên dưới nhé!
Xem thêm video
Lý thuyết mệnh đề toán 10
- Phép phủ định
- Phép giao
- Phép kéo theo
- Phép hợp
Bài tập mệnh đề toán lớp 10
- Chứng minh tính đúng sai của mệnh đề bằng phương pháp dùng trực tiếp định nghĩa.
- Chứng minh tính đúng sai mệnh đề bằng phương pháp qui nạp
- Chứng minh tính đúng sai mệnh đề bằng phương pháp phản chứng
Tham khảo
1. ↑https://vi.wikipedia.org/wiki/M%E1%BB%87nh_%C4%91%E1%BB%81_to%C3%A1n_h%E1%BB%8Dc
2. ↑https://toanhoc247.com/ly-thuyet-va-bai-tap-ve-menh-de-toan-lop-10-a3836.html
3. ↑https://loigiaihay.com/ly-thuyet-ve-menh-de-c45a4751.html



 056.3753648
056.3753648
 Chat FB
Chat FB