Tóm tắt tài liệu
Góc giữa hai đường thẳng chéo nhau trong không gian là một dạng toán khá quan trọng trong chương trình toán THPT. Đặc biệt là chương trình hình học lớp 11 chương số 3. Tài liệu dưới đây sẽ cung cấp các phương pháp giải bài tập loại này và một số ví dụ điển hình. Qua tài liệu có thể giúp các em hiểu hơn về hình học không gian cũng như một số tư duy và kĩ năng được trình bày.
1. Phương pháp xác định góc giữa hai đường thẳng chéo nhau
- Góc giữa đường thẳng SA và mặt phẳng (P) là góc tạo bởi đường thẳng SA và hình chiếu SB của nó trên mặt phẳng (P). Tức là
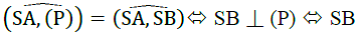chính là hình chiếu của SA trên mặt phẳng (P) . - Góc giữa hai mặt phẳng là góc giữa hai đường thẳng cắt nhau nằm trong hai mặt phẳng đó và cùng vuông góc với giao tuyến của hai mặt phẳng
- Góc giữa hai đường thẳng chéo nhau là góc tạo bởi một đường thẳng này và một đường thẳng song song với đường thẳng kia
- Hoặc giữa hai đường thẳng chéo nhau là góc giữa hai đường thẳng cắt nhau và cùng song song với hai đường thẳng kia
2. Bài tập minh họa
Bài 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA = a , SB = a√3 và mặt phẳng (SAB) vuông góc với mặt phẳng đáy . Gọi M , N lần lượt là trung điểm của các cạnh AB , BC . Tính theo a thể tích của khối chóp S.BMDN và tính cosin của góc giữa hai đường thẳng SM , DN .
Bài 2:
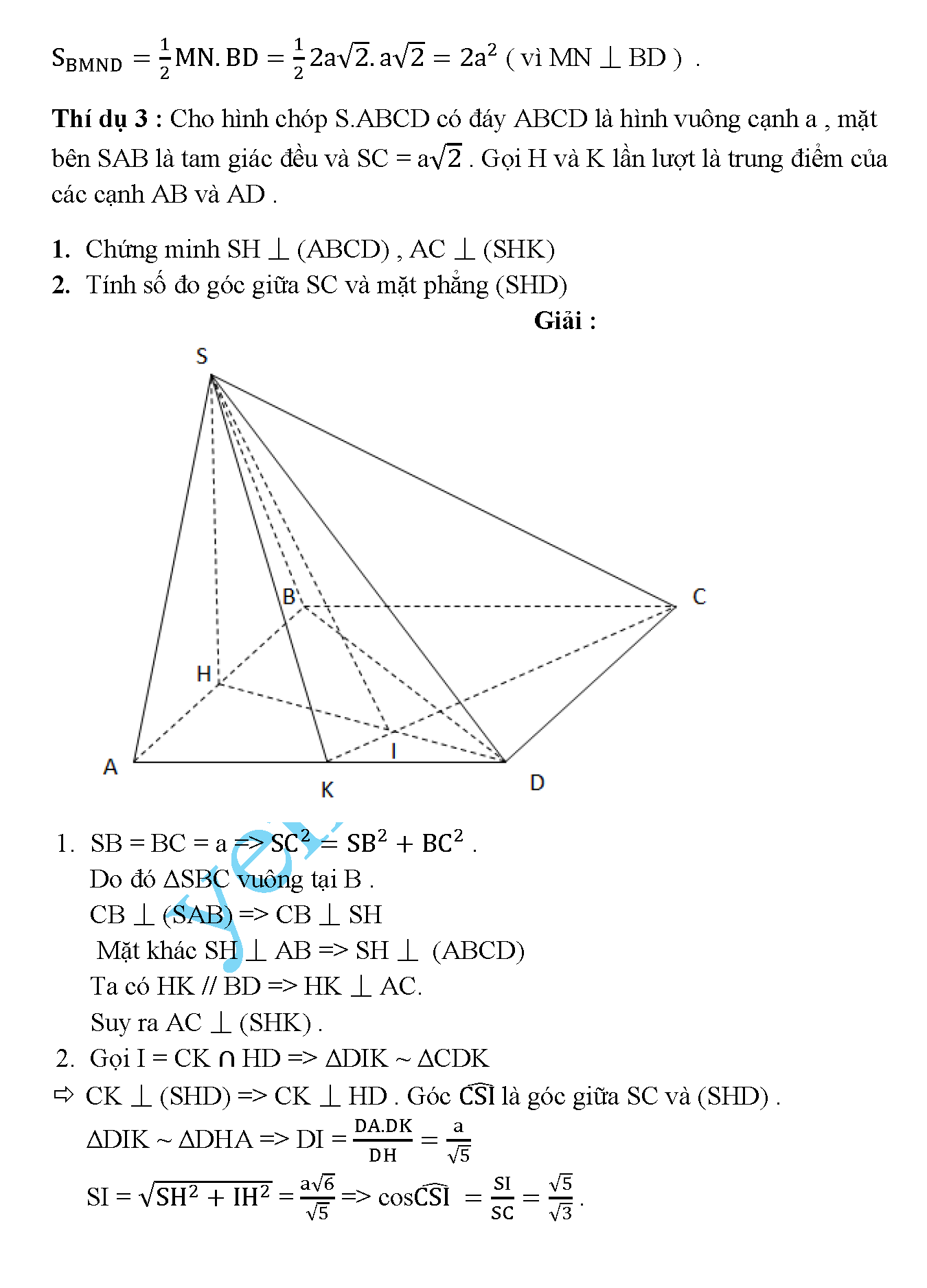
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều và SC = a√3 . Gọi H và K lần lượt là trung điểm của các cạnh AB và AD.
1.Chứng minh SH ⏊ (ABCD) , AC ⏊ (SHK)
2.Tính số đo góc giữa SC và mặt phẳng (SHD)
Bài 3:
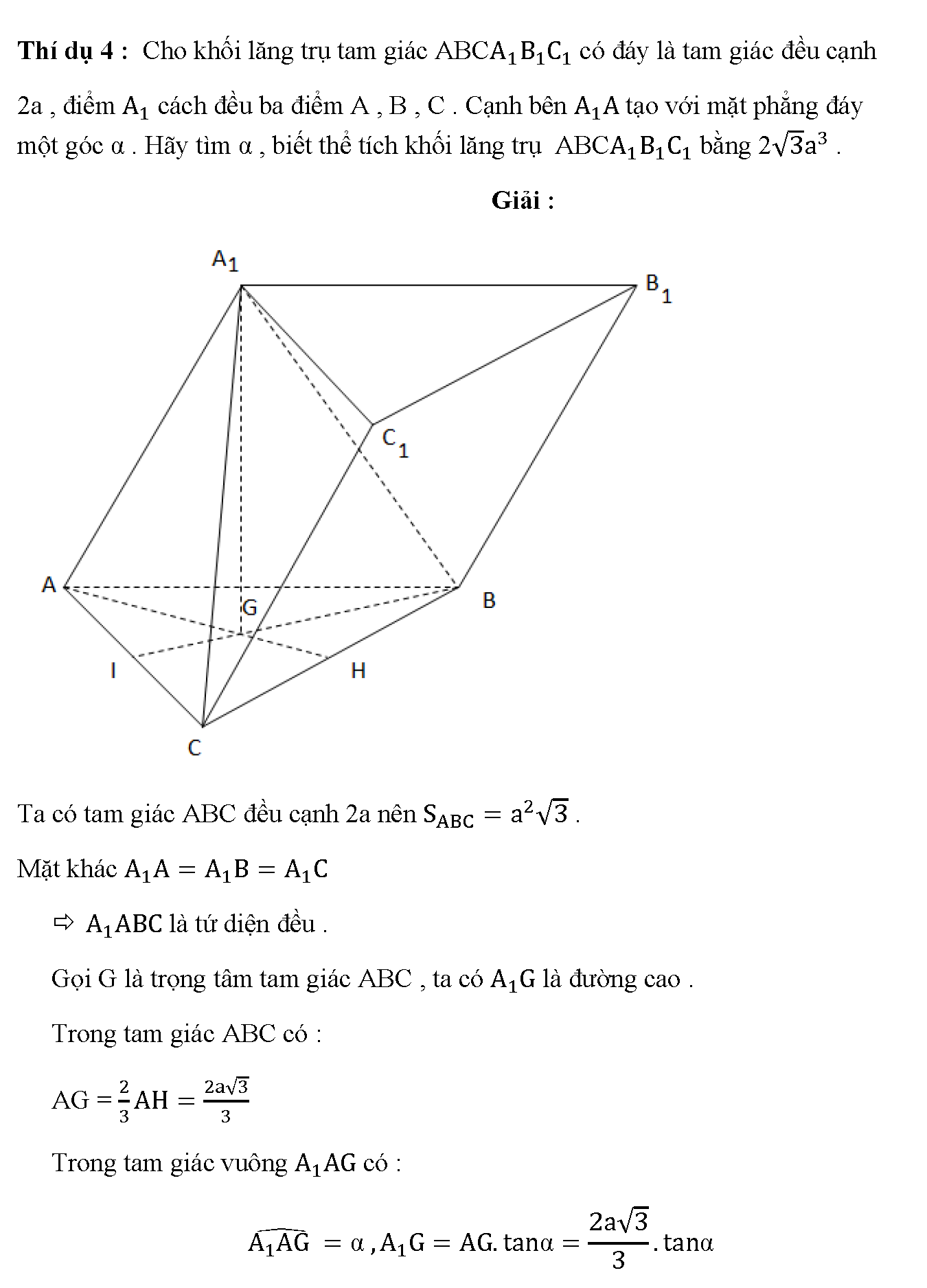
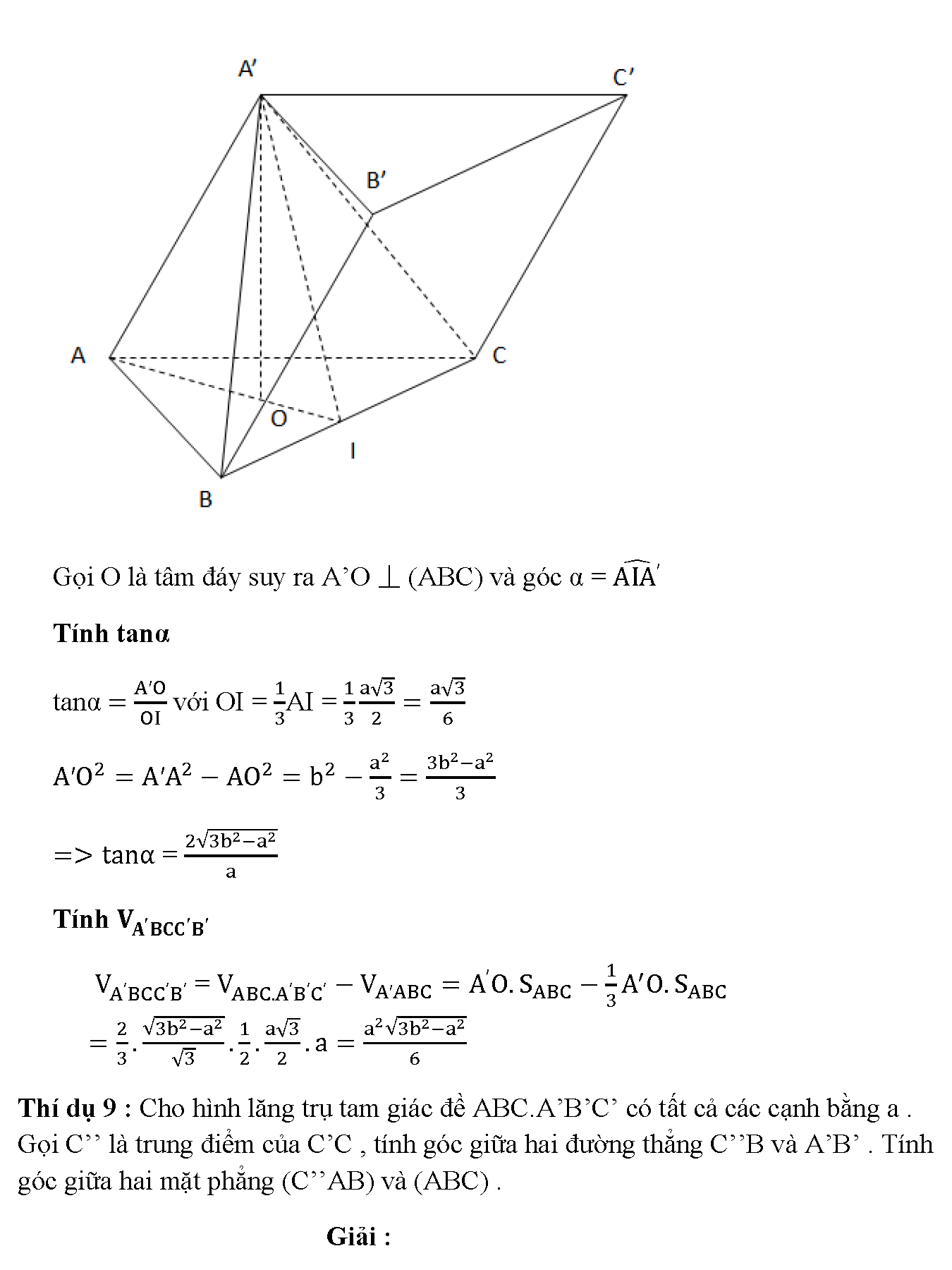
Cho khối lăng trụ tam giác ABC.A1B1C1 có đáy là tam giác đều cạnh 2a, điểm cách đều ba điểm A , B , C . Cạnh bên tạo với mặt phẳng đáy một góc α . Hãy tìm α , biết thể tích khối lăng trụ ABC bằng 2√3.
Bài 4:
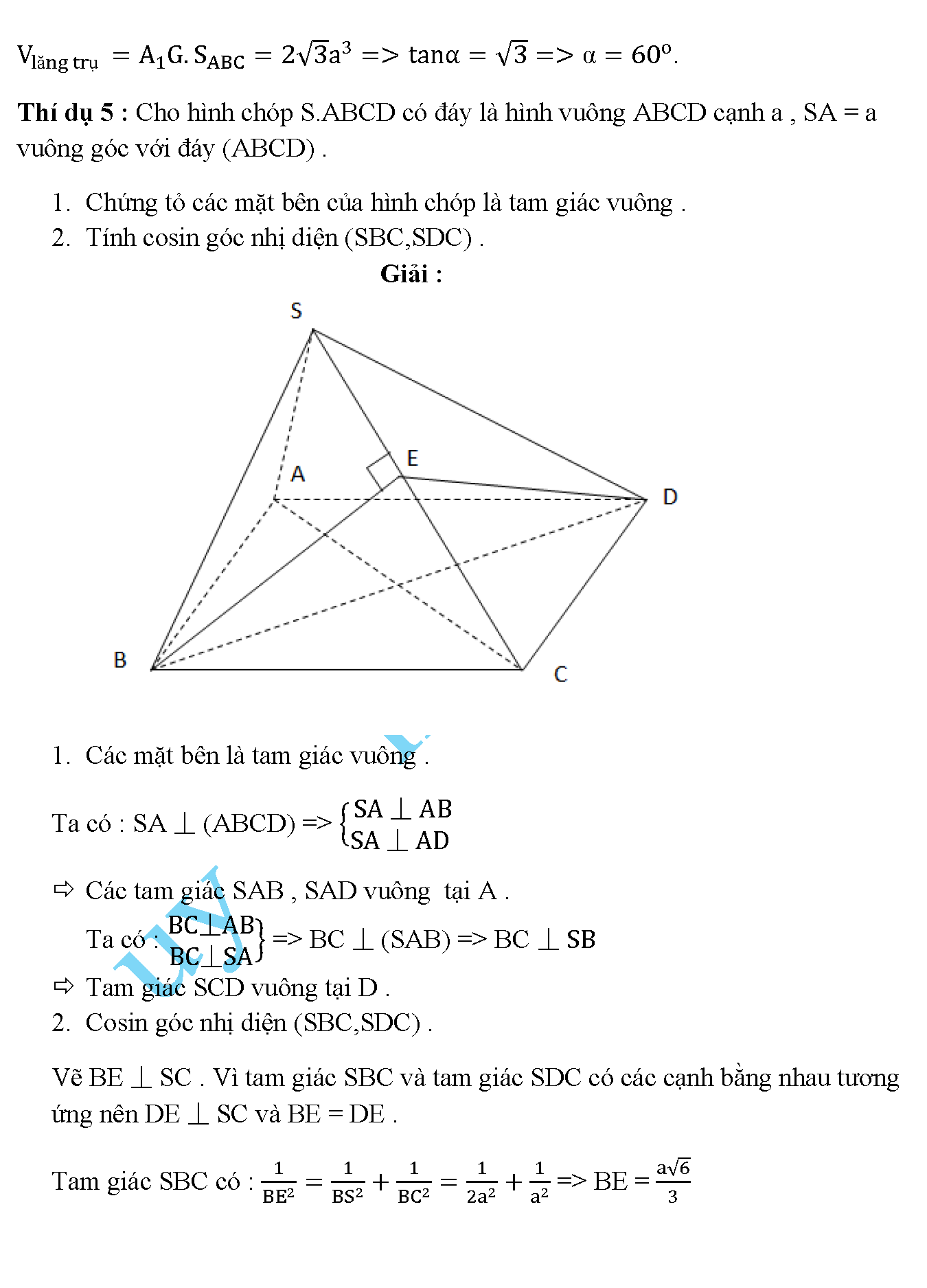
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a , SA = a vuông góc với đáy (ABCD) .
1.Chứng tỏ các mặt bên của hình chóp là tam giác vuông .
2.Tính cosin góc nhị diện (SBC,SDC) .
Bài 5:
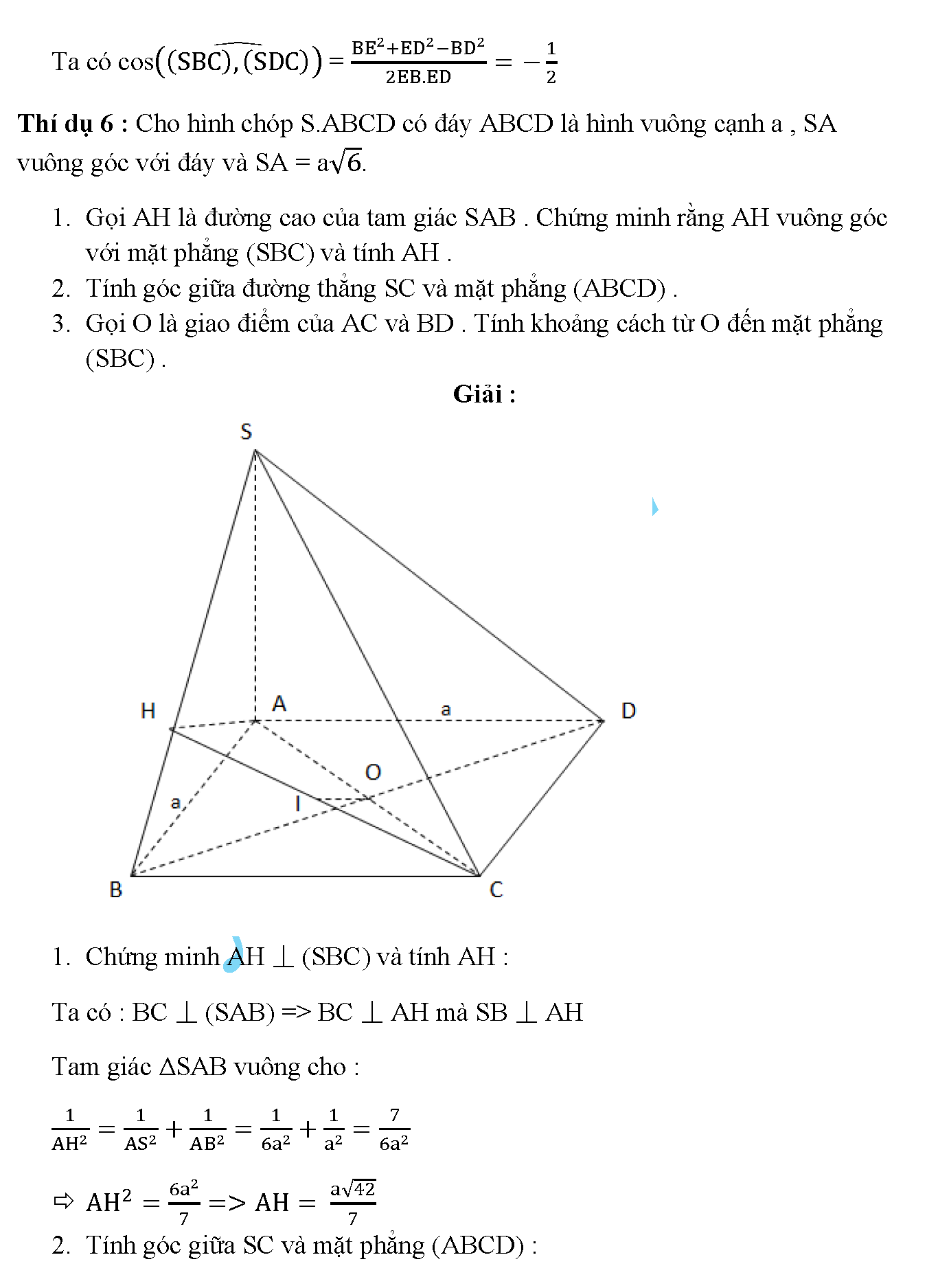
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA = a√3 .
1.Gọi AH là đường cao của tam giác SAB. Chứng minh rằng AH vuông gócvới mặt phẳng (SBC) và tính AH.
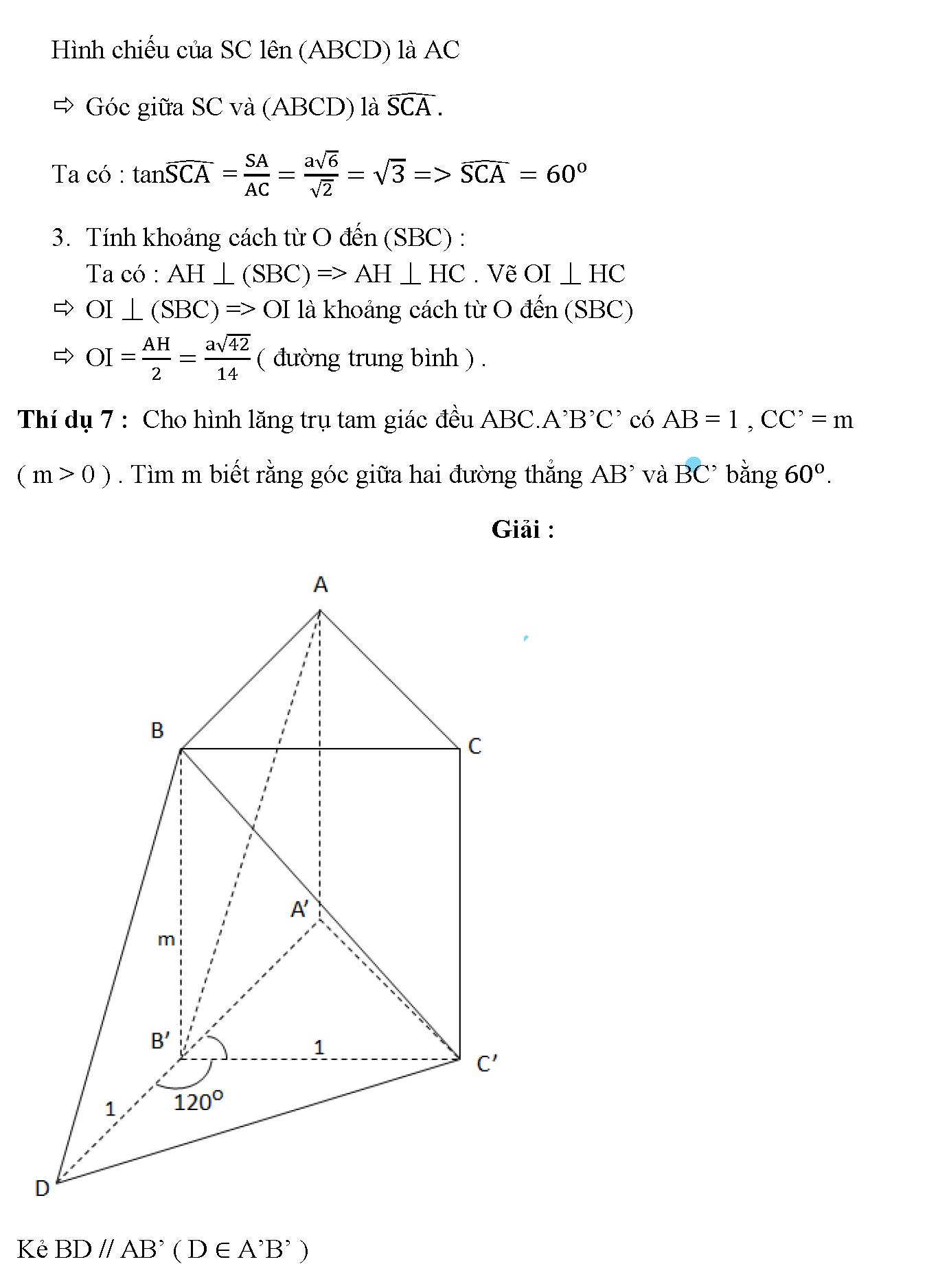
2.Tính góc giữa đường thẳng SC và mặt phẳng (ABCD) .
3.Gọi O là giao điểm của AC và BD . Tính khoảng cách từ O đến mặt phẳng(SBC).
3. Bài tập có lời giải về cách xác định góc giữa 2 đường thẳng chéo nhau
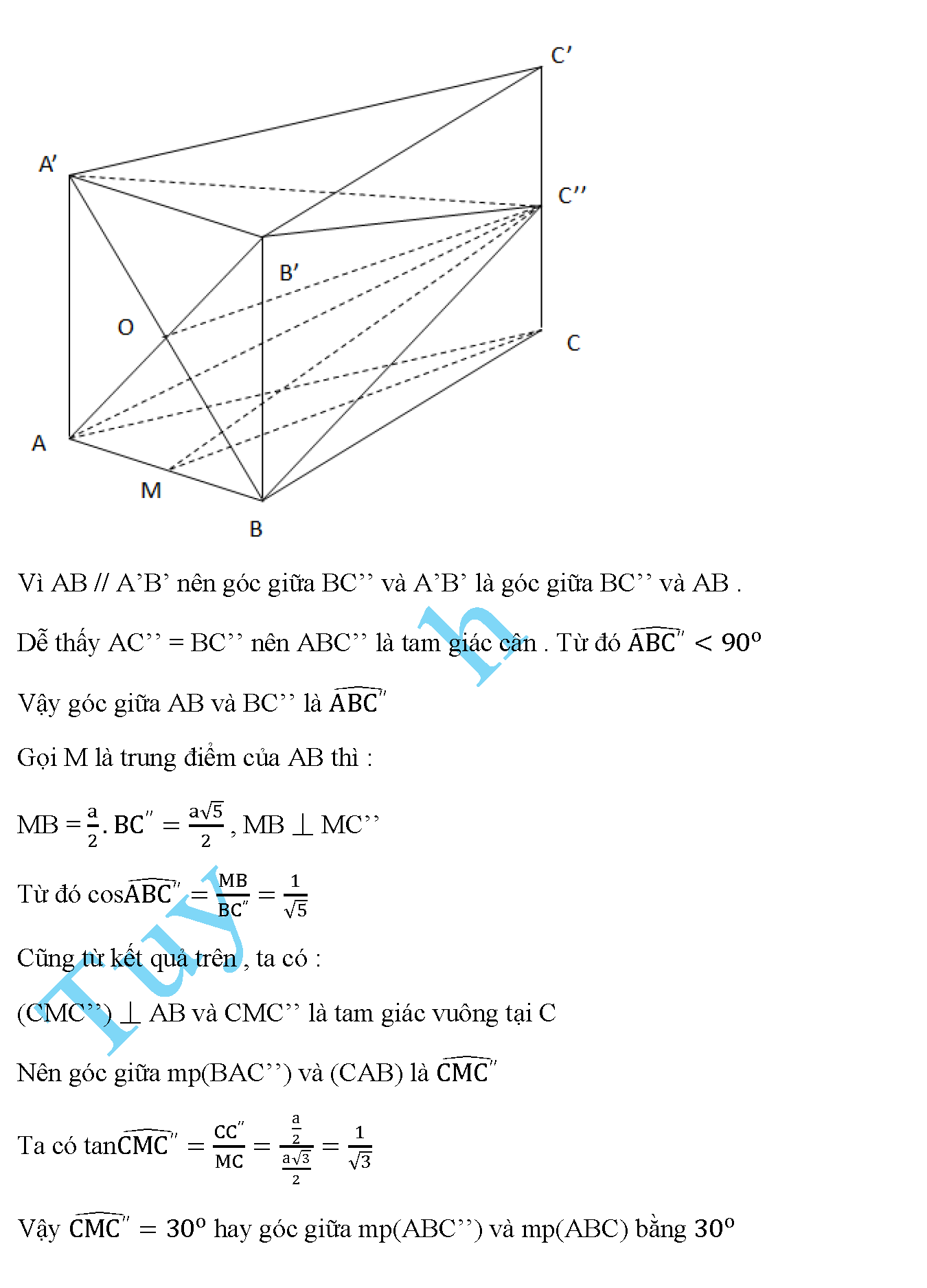
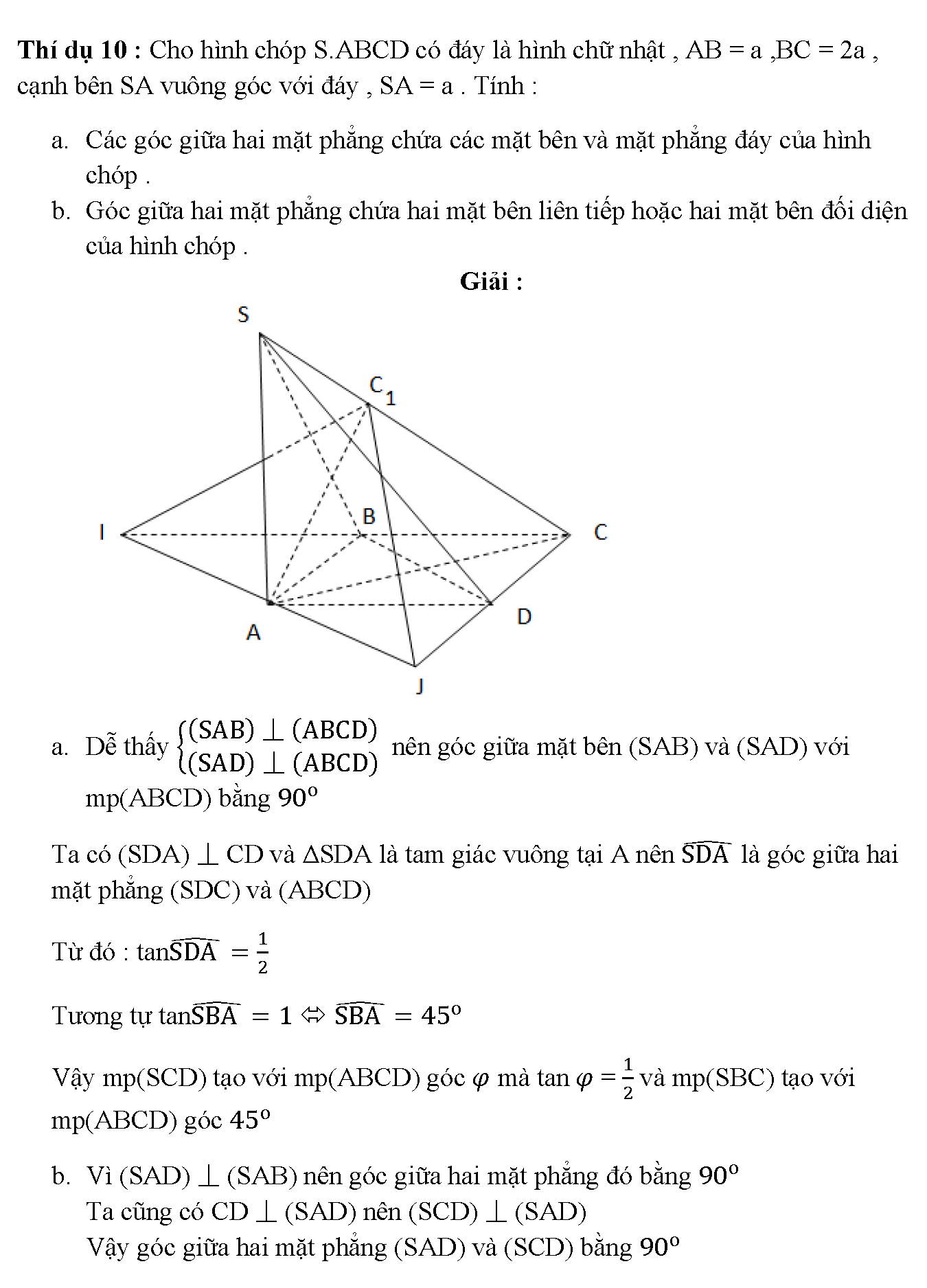
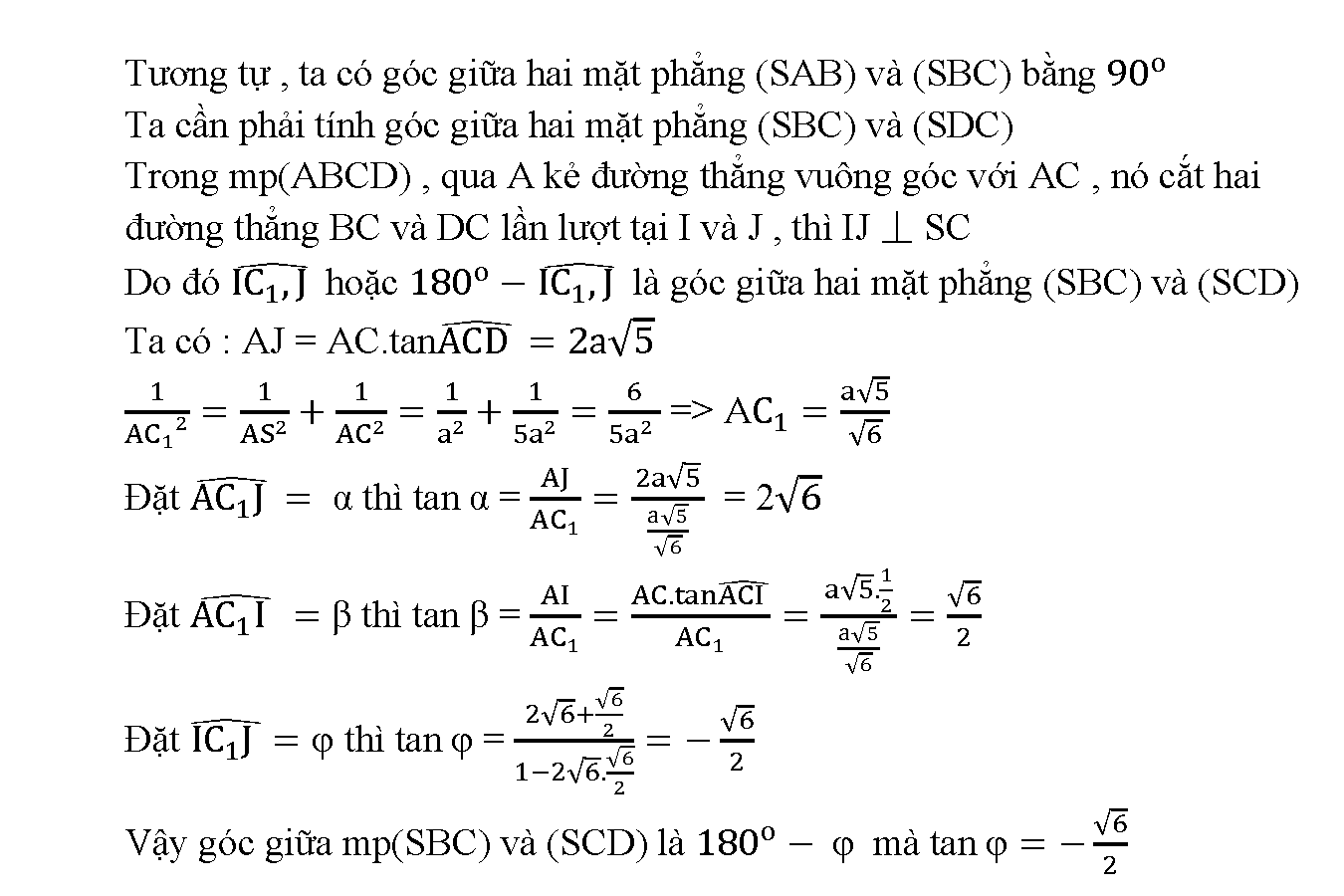
Vậy là chúng ta vừa tìm hiểu xong các loại bài tập về góc giữa hai đường thẳng chéo nhau. Đây là một dạng toán nhỏ trong những bài toán lớn. Tuy nhiên nó chiếm một vai trò khá quan trọng. Khi hình học không gian nói riêng và hình học phẳng nói chung đề là sự kế thừa từ câu trước. Thì các loại bài tập nhỏ sẽ khiến học sinh khá loay hoay mỗi khi suy nghĩ. Do đó chúng ta cần phải thật cẩn thận khi học bất kì dạng toán nào. Và đặc biệt, làm bài tập càng nhiều càng tốt để luyện tập phản xạ, tư duy. Chúc các em học tốt.
Từ khóa:
- góc giữa 2 đường thẳng chéo nhau trong tứ diện đều
- tính góc giữa 2 đường thẳng bằng vecto
- trắc nghiệm góc giữa hai đường thẳng
- góc giữa 2 đường thẳng trong hình lăng trụ
- cách xác định góc giữa đường thẳng và mặt phẳng
- khoảng cách giữa 2 đường thẳng chéo nhau
- cách xác định góc giữa đường thẳng và mặt phẳng trong lăng trụ
- cho hai đường thẳng tìm m để góc giữa hai đường thẳng đó với
056.3753648
Chat FB