Tóm tắt tài liệu
Là một trong 7 dạng vô định, giới hạn hàm số dạng vô cùng trên vô cùng (\[\frac{\infty }{\infty }\]) là một dạng khá hay gặp trong các bài toán về giới hạn. Đặc biệt là trong các đề thi giữa kì, cuối kì và cả thi trung học phổ thông quốc gia. Ở dạng toán này, chúng ta hoàn toàn có thể tính bằng casio. Tuy nhiên, để hiểu bản chất cũng như áp dụng trong các bài toán khó hơn, các em cần hiểu bản chất. Bài viết sau sẽ giúp các em điều này
Giới hạn của hàm số dạng vô cùng trên vô cùng
Cho hàm số \[f(x),g(x)\] thõa mãn \[\underset{x\to \infty }{\mathop{\lim }}\,f(x)=\infty \] và \[\underset{x\to \infty }{\mathop{\lim }}\,f(x)=\infty \].
Khi đó \[\underset{x\to \infty }{\mathop{\lim }}\,\frac{f(x)}{g(x)}\] có dạng vô cùng trên vô cùng \[\frac{\infty }{\infty }\]
Trường hợp 1: y = f(x)/g(x) là hàm số hữu tỉ
Phương án chung cho loại bài tập này là chia cả tử và mẫu cho lũy thừa bậc cao nhất rồi áp dụng tính chất giới hạn của dãy số.
Trường hợp 2: y = f(x)/g(x) là hàm số vô tỉ
Giả sử bậc của căn thức là m, bậc cao nhất của ẩn trong căn là n. Các bạn lấy thương của m/n và coi đây là bậc của căn thức đó. Sau đó chúng ta sẽ lấy cả tử và mẫu chia cho lũy thừa cao nhất. Bạn cũng có thể áp dụng phương pháp đặt nhân tử chung hoặc đơn giản biểu thức.
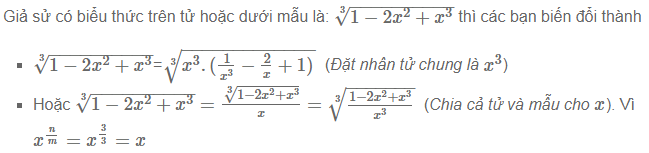
Bài tập giới hạn của hàm số dạng vô cùng trên vô cùng
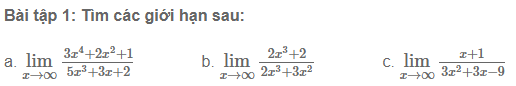

Để xem thêm nhiều bài tập giới hạn hàm số dạng vô cùng trên vô cùng khác để nắm rõ cách giải, qui luật và cách tính nhanh. Các em có thể xem thêm các bài viết và tài liệu tham khảo thêm ở phía bên dưới.
Bài viết có sử dụng nguồn: http://hoctoan24h.net/gioi-han-ham-so-dang-vo-cung-tren-vo-cung/



 056.3753648
056.3753648
 Chat FB
Chat FB