Tóm tắt tài liệu
Tính đơn điệu của hàm số là một chuyên đề không thể thiếu trong các đề thi toán lớp 12, đặc biệt trong các đề thi đại học. Bài viết này sẽ trình bày cho các em một số vấn đề sau:
- Lý thuyết tính đơn điệu của hàm số
- Xét sự biến thiên của hàm số không chứa tham số (cơ bản)
- Xét sự biến thiên của hàm số chứa tham số (nâng cao)
Lý thuyết tính đơn điệu của hàm số
- Hàm số \[y=f(x),\] đồng biến trên \[(a,b)\] \[\Leftrightarrow \] \[f'(x)\ge 0\] \[\forall x\in (a,b)\] và \[f'(x)=0\] tại một số hữu hạn điểm thuộc \[(a,b)\]
- Hàm số \[y=f(x),\] nghịch biến trên \[(a,b)\] \[\Leftrightarrow \] \[f'(x)\le 0\] \[\forall x\in (a,b)\] và \[f'(x)=0\] tại một số hữu hạn điểm thuộc \[(a,b)\]
Dạng 1: Xét sự biến thiên của hàm số không chứa tham số
*) Phương pháp giải: Để xét tính đơn điệu của hàm số \[y=f(x)\] trên khoảng bất kì ta làm như sau:
- Tìm TXĐ \[K\] của hàm số
- Tìm ra biểu thức của \[y’\]
- Giải phương trình \[y’=0\]
- Lập bảng biến thiên và kết luận.
Ví dụ 1: Xét tính đơn điệu của hàm số sau: \[y=f(x)=\frac{{{x}^{2}}-x-1}{x-1}\]
- Tập xác định \[D=R\backslash \text{ }\!\!\{\!\!\text{ }1\}\]
- \[y’=\frac{{{x}^{2}}-2x}{{{(x-1)}^{2}}}\]
- \[y’=0\Leftrightarrow \left[ \begin{matrix}x=0 \\x=\frac{1}{2} \\\end{matrix} \right.\]
Dễ thấy dấu của hàm số \[y=f(x)\] phụ thuộc vào biểu thức \[{{x}^{2}}-2x\]. Ta tính một số giới hạn cơ bản rồi vẽ bảng biến thiên
- \[\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{x-1+\frac{1}{x}}{1-\frac{1}{x}}=+\infty \]
- \[\underset{x\to -\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{x-1+\frac{1}{x}}{1-\frac{1}{x}}=+\infty \]
- \[\underset{x\to {{\frac{1}{2}}^{-}}}{\mathop{\lim }}\,f(x)=+\infty ,\underset{x\to {{\frac{1}{2}}^{+}}}{\mathop{\lim }}\,f(x)=-\infty \]
Bảng biến thiên
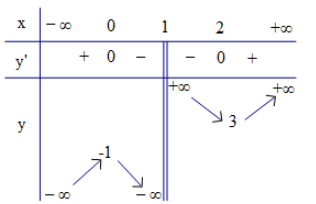
Kết luận:
- Hàm số đồng biến trên \[(-\infty ;0)\] và \[(2;+\infty )\]
- Hàm số nghịch biến trên \[(0;1)\] và \[(1;2)\]
Ví dụ 2: Tìm các khoảng đồng biến, nghịch biến của hàm số \[y=2x+\sqrt{1-{{x}^{2}}}\]
- \[TX\text{D}=\text{ }\!\![\!\!\text{ }-1;1]\]
- \[{y}’=2-\frac{x}{\sqrt{1-{{x}^{2}}}}=\frac{2.\sqrt{1-{{x}^{2}}}-x}{\sqrt{1-{{x}^{2}}}}\], \[\forall x\in (-1;1)\]
- \[y’=0\Leftrightarrow x=\frac{2}{\sqrt{5}}\]
- Lập bảng biến thiên:
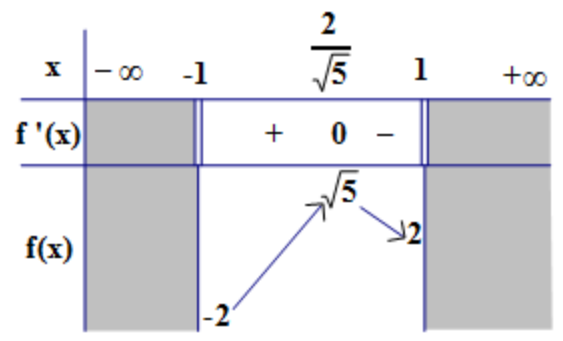
Kết luận:
- Hàm số đã cho đồng biến trên: \[\left( -1;\frac{2}{\sqrt{5}} \right)\]
- Hàm số đã cho nghịch biến trên: \[\left( \frac{2}{\sqrt{5}};1 \right)\]
Lưu ý:
Khi xét dấu \[{f}'(x)\] trong các khoảng, để biết \[{f}'(x)\] mang dấu (+) hay (-), ta chỉ cần lấy một số bất kì thuộc khoảng đang xét, sau đó tính \[{f}'(x)\] tại điểm đó.
Dạng 2: Xét sự biến thiên của hàm số chứa tham số
Lý thuyết về tính đơn điệu của hàm số:
- Hàm số \[y=f(x),\] đồng biến trên \[(a,b)\] \[\Leftrightarrow \] \[f'(x)\ge 0\] \[\forall x\in (a,b)\] và \[f'(x)=0\] tại một số hữu hạn điểm thuộc \[(a,b)\]
- Hàm số \[y=f(x),\] nghịch biến trên \[(a,b)\] \[\Leftrightarrow \] \[f'(x)\le 0\] \[\forall x\in (a,b)\] và \[f'(x)=0\] tại một số hữu hạn điểm thuộc \[(a,b)\]
Kiến thức liên quan
+) Định lý về dấu của tham thức bậc hai: Cho hàm số bậc hai \[f(x)=a.{{x}^{2}}+bx+c\] với định thức \[\Delta ={{b}^{2}}-4ac\]
- Nếu \[\Delta <0\] thì \[f(x)\] luôn cùng dấu với \[a\]
- Nếu \[\Delta =0\] thì \[f(x)\] luôn cùng dấu với \[a\] (ngoại trừ \[x=-\frac{b}{2a}\])
- Nếu \[\Delta >0\] thì \[f(x)\] có 2 nghiệm \[{{x}_{1}},{{x}_{2}}\]. Trong khoảng hai nghiệm \[{{x}_{1}},{{x}_{2}}\] thì cùng dấu với \[a\], ngoài khoảng \[{{x}_{1}},{{x}_{2}}\] ngược dấu với \[a\].
+) Định lí Vi-et:
Cho \[{{x}_{1}},{{x}_{2}}\] là nghiệm của phương trình \[f(x)=a.{{x}^{2}}+bx+c=0\], khi đó ta có:
\[\left\{ \begin{matrix}{{x}_{1}}+{{x}_{2}}=-\frac{b}{a} \\{{x}_{1}}.{{x}_{2}}=\frac{c}{a} \\\end{matrix} \right.\]
+) Nguyên tắc so sánh nghiệm \[{{x}_{1}},{{x}_{2}}\] với \[\alpha \] được tổng hợp như sau:
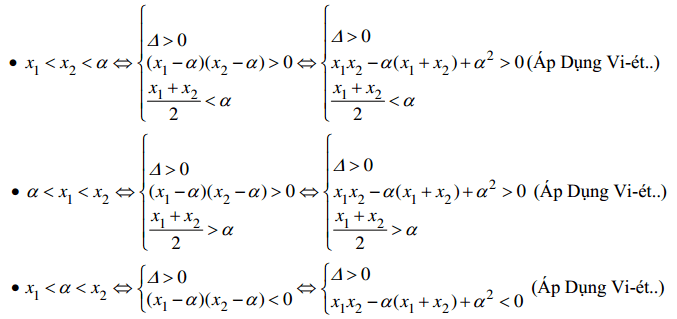
+) Tìm khoảng điều kiện của m:
- \[m\le f(x),\forall x\in D\Leftrightarrow m\le \underset{x\in D}{\mathop{Min.f(x)}}\,\]
- \[m\ge f(x),\forall x\in D\Leftrightarrow m\ge \underset{x\in D}{\mathop{Max.f(x)}}\,\]
Ví dụ 1: Cho hàm số \[y=-\frac{2}{3}{{x}^{3}}+(m+1){{x}^{2}}+2mx+5\] với \[m\] là hằng số thực. Tìm m để hàm số đã cho đồng biến trên khoảng \[(0;2)\].
Cách 1: Vì hàm số \[y'(x)\] liên tục tại điểm \[x=0\] và tại điểm \[x=2\] nên ta có \[y’\ge 0\] \[\forall x\in \text{ }\!\![\!\!\text{ }0;2]\]
\[\Leftrightarrow -2{{x}^{2}}+2(m+1)x+2m\ge 0\], \[\forall x\in \text{ }\!\![\!\!\text{ }0;2]\]
\[\Leftrightarrow m.(x+1)\ge {{x}^{2}}-x\], \[\forall x\in \text{ }\!\![\!\!\text{ }0;2]\]
\[\Leftrightarrow m\ge g(x)\], \[\forall x\in \text{ }\!\![\!\!\text{ }0;2]\] ( với \[g(x)=\frac{{{x}^{2}}-x}{x+1}\])
\[\Leftrightarrow m\ge \underset{\text{ }\!\![\!\!\text{ }0;2]}{\mathop{Max.g(x)}}\,\]
Xét hàm số \[g(x)=\frac{{{x}^{2}}-x}{x+1}\] trên đoạn \[[0;2]\]
\[\Rightarrow g'(x)=\frac{{{x}^{2}}+2x-1}{{{(x+1)}^{2}}}\] \[\Rightarrow g'(x)=0\] \[\Leftrightarrow x=-1+\sqrt{2}\], \[\forall x\in \text{ }\!\![\!\!\text{ }0;2]\]
Ta có:
- \[g(0)=0\]
- \[g(2)=\frac{2}{3}\]
- \[g(-1+\sqrt{2})=-3+2\sqrt{2}\]
\[\Rightarrow \underset{0\to +\infty }{\mathop{Max.g(x)}}\,=\frac{2}{3}\] tại \[x=2\].
Vậy \[m\ge \frac{2}{3}\] thì hàm số đồng biến trên khoảng \[(0;2)\].
Cách 2: Sử dụng định lý dấu tam thức bậc hai
Ta có: \[y’=-2{{x}^{2}}+2(m+1)x+2m\], với \[\Delta ‘={{m}^{2}}+6m+1\]
\[\Rightarrow \] hàm số đồng biến trên khoảng \[(0;2)\] \[\Leftrightarrow y’\ge 0\] \[\forall x\in (0;2)\] (*)
TH1: \[\Delta ‘\le 0\] \[\Leftrightarrow {{m}^{2}}+6m+1\le 0\] \[\Leftrightarrow -3-2\sqrt{2}\le x\le -3+2\sqrt{2}\]
\[\Rightarrow \] Theo định lý về dấu tam thức bậc hai ta có \[y’\le 0\] \[\forall x\in R\]
TH2: \[\Delta ‘>0,\] \[\Leftrightarrow \] \[{{m}^{2}}+6m+1>0\] \[\Leftrightarrow \] \[\left[ \begin{matrix}m<-3-2\sqrt{2} \\m>-3-2\sqrt{2} \\\end{matrix} \right.\] thì \[*\] đúng, khi đó \[y’=0\] có hai nghiệm \[{{x}_{1}},{{x}_{2}}\] sao cho \[({{x}_{1}}<{{x}_{2}})\] và \[{{x}_{1}}\le 0<2\le {{x}_{2}}\].



 056.3753648
056.3753648
 Chat FB
Chat FB