Tóm tắt tài liệu
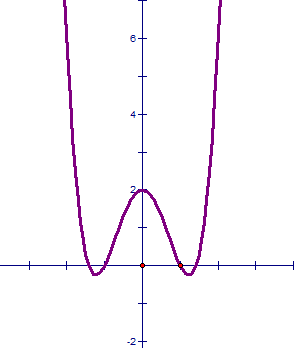
Để tìm cực trị hàm trùng phương, đầu tiên ta cùng tìm hiểu dạng của hàm số này:
\[y=a.{{x}^{4}}+b.{{x}^{2}}+c\]
I. Cực trị hàm số trùng phương
– Trường hợp 1: \[\left\{ \begin{matrix}ab\ge 0 \\{{a}^{2}}+{{b}^{2}}>0 \\\end{matrix} \right.\] \[\Rightarrow \] Hàm số có một điểm cực trị duy nhất.
– Trường hợp 2: \[ab<0\] \[\Rightarrow \] Hàm số có 3 điểm cực trị
– Khi hàm số có 3 điểm cực trị thì hoành độ 3 điểm cực trị là: \[0;-\sqrt{\frac{-b}{2a}};\sqrt{\frac{-b}{2a}}\]
– Khi đó, tọa độ 3 điểm cực trị tương ứng: \[\left\{ \begin{matrix}A(0;c) \\B\left( -\sqrt{\frac{-b}{2a}};c-\frac{{{b}^{2}}}{4a} \right);C\left( \sqrt{\frac{-b}{2a}};c-\frac{{{b}^{2}}}{4a} \right) \\\end{matrix} \right.\]
♦ Nhận xét:
\[\Delta ABC,\] cân tại \[A\], có \[A\in Oy\], khi đó \[AB=AC=\sqrt{\frac{{{b}^{4}}-8ab}{16{{a}^{2}}}},BC=\sqrt{\frac{-b}{2a}}\]
– Các điểm cực trị đồ thị hàm số thuộc các trục tọa độ \[\Leftrightarrow {{b}^{2}}=4ac\]
– Điểm \[(0;{{y}_{0}})\] là trọng tâm \[\Delta ABC\] \[\Leftrightarrow \] \[3{{y}_{0}}=3c-\frac{{{b}^{2}}}{2a}\]
– Điểm \[(0;{{y}_{0}})\] là trực tâm \[\Delta ABC\] \[\Leftrightarrow \] \[{{y}_{0}}-c=-\frac{8a+{{b}^{3}}}{4ab}\]
– Điểm \[(0;{{y}_{0}})\] là tâm đường tròn ngoại tiếp \[\Delta ABC\] \[\Leftrightarrow \] \[{{y}_{0}}-c=\frac{8a-{{b}^{3}}}{4ab}\]
Do đó \[Cos\widehat{BAC}=\frac{{{b}^{3}}+8a}{{{b}^{3}}-8a},{{S}_{ABC}}=\sqrt{\frac{-{{b}^{5}}}{32{{a}^{3}}}}\]
– \[\Delta ABC,\] vuông tại A \[\Leftrightarrow Cos\widehat{BAC}=0\Leftrightarrow {{b}^{3}}=-8a\]
– \[\Delta ABC\] đều \[\Leftrightarrow \]\[Cos\widehat{BAC}=\frac{1}{2}\Leftrightarrow {{b}^{3}}=-24a\]
– \[\Delta ABC\] có một góc \[{{120}^{0}}\]\[\Leftrightarrow Cos\widehat{BAC}=-\frac{1}{2}\Leftrightarrow 3{{b}^{3}}=8a\]
II. Giao điểm với trục hoành
Với \[ab<0,ac>0,{{b}^{2}}-4ac>0\], đồ thị hàm số trùng phương cắt trục hoành tại 4 điểm phân biệt. Khi đó:
– Hoành độ 4 giao điểm lập thành cấp số cộng \[\Leftrightarrow 9{{b}^{2}}=100ac\]
– Cắt trục hoành tại 4 điểm phân biệt, tạo thành 3 đoạn thẳng có độ dài bằng nhau \[\Leftrightarrow 9{{b}^{2}}=100ac\].
– Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành có phần phía trên Ox và phần phía dưới Ox bằng nhau \[\Leftrightarrow \] \[5{{b}^{2}}=100ac\]
III. Một số công thức tính nhanh của cực trị hàm số trung phương
– Đặt \[\widehat{BAC}=\alpha \]
– Tổng quát: \[{{\cot }^{2}}\frac{\alpha }{2}=\frac{-{{b}^{3}}}{8a}\]
– Bảng một số công thức tính nhanh cực trị hàm số trùng phương
| Dữ kiện | Các công thức thõa mãn \[ab<0\] |
| Cho tam giác \[ABC\] vuông cân tại \[A\] | \[{{b}^{3}}=8a\] |
| Cho tam giác \[ABC\] đều | \[{{b}^{3}}=24a\] |
| Cho tam giác \[ABC\] có diện tích \[{{S}_{\Delta ABC}}={{S}_{0}}\] | \[32{{a}^{3}}{{({{S}_{0}})}^{2}}+b{}^{3}=0\] |
| Cho tam giác \[ABC\] có diện tích \[\max ({{S}_{0}})\] | \[{{S}_{0}}=\sqrt{-\frac{32{{b}^{5}}}{{{a}^{3}}}}\] |
| Cho tam giác \[ABC\] có bán kính đường tròn nội tiếp \[{{r}_{\Delta ABC}}={{r}_{0}}\] | \[r=\frac{{{b}^{2}}}{4.\left| a \right|.\left( 1+\sqrt{1-\frac{{{b}^{3}}}{8a}} \right)}\] |
| Cho tam giác \[ABC\] có bán kính đường tròn ngoại tiếp \[{{R}_{\Delta ABC}}=R\] | \[R=\frac{{{b}^{3}}-8a}{8\left| a \right|b}\] |
| Cho tam giác \[ABC\] có độ dài cạnh \[BC={{m}_{0}}\] | \[a.{{m}_{0}}^{2}+2b=0\] |
| Cho tam giác \[ABC\] có độ dài cạnh \[AB=AC={{n}_{0}}\] | \[16{{a}^{2}}.{{n}_{0}}^{2}-{{b}^{4}}+8ab=0\] |
| Cho tam giác \[ABC\] có cực trị \[B,C\in Ox\] | \[{{b}^{2}}=4ac\] |
| Cho tam giác \[ABC\] có \[3\] góc nhọn | \[b(8a+{{b}^{3}})>0\] |
| Cho tam giác \[ABC\] có trọng tâm \[O\] | \[{{b}^{2}}=6ac\] |
| Cho tam giác \[ABC\] có trực tâm \[O\] | \[{{b}^{3}}+8a-4ac=0\] |
| Cho tam giác \[ABC\] có cùng điểm \[O\] tạo thành hình thoi | \[{{b}^{2}}=2ac\] |
| Cho tam giác \[ABC\] có \[O\] là tâm đường tròn nội tiếp | \[{{b}^{3}}-8a-4abc=0\] |
| Cho tam giác \[ABC\] có \[O\] là tâm đường tròn ngoại tiếp | \[{{b}^{3}}-8a-8abc=0\] |
| Cho tam giác \[ABC\] có \[BC=kAB=kAC\] | \[{{b}^{3}}.{{k}^{2}}-8a({{k}^{2}}-4)=0\] |
| Trục hoành chia tam giác \[ABC\] thành hai phần có diện tích bằng nhau | \[{{b}^{2}}=4\sqrt{2}\left| ac \right|\] |
| Cho tam giác \[ABC\] có điểm cực trị cách đều trục hoành | \[{{b}^{2}}=8ac\] |
| Đồ thị hàm số \[(C):y=a{{x}^{4}}+b{{x}^{2}}+c\] cắt trục \[Ox\] tại 4 điểm phân biệt lập thành cấp số cộng | \[{{b}^{2}}=\frac{100}{9}ac\] |
| Định tham số để hình phẳng giới thiệu bởi đồ thị \[(C):y=a{{x}^{4}}+b{{x}^{2}}+c\] và trục hoành có diện tích phần trên và phần dưới bằng nhau | \[{{b}^{2}}=\frac{36}{5}ac\] |
| Phương trình đường tròn ngoại tiếp \[ABC\] | \[{{x}^{2}}+{{y}^{2}}-\left( \frac{2}{b}-\frac{\Delta }{4a}+c \right)y+c\left( \frac{2}{b}-\frac{\Delta }{4a} \right)=0\] |
Bảng trên tổng hợp các công thức tính nhanh phần cực trị hàm số trùng phương. Chúng tôi vẫn khuyến khích các em học sinh tự thành lập công thức và áp dụng linh hoạt vào bài tập. Công thức bên trên chỉ để giải quyết những bài toán khó, với áp lực thời gian!
Chuyên mục: Cực trị hàm số
Xem thêm video
Từ khóa: cực trị hàm số hàm trùng phương, công thức tính nhanh hàm trùng phương, trùng phương.



 056.3753648
056.3753648
 Chat FB
Chat FB