Tóm tắt tài liệu
Chuyên đề phương trình đường thẳng lớp 10 là một chuyên đề có lượng kiến thức khá quan trọng; là nền tảng cho các em học phương trình tọa độ xyz sau này, vì thế bài này tailieure sẽ tổng hợp đầy đủ các điểm lý thuyết trọng tâm.
1. Vectơ chỉ phương của đường thẳng
Định nghĩa :
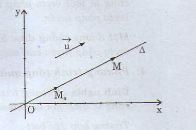
Vectơ \[{\vec{u}}\] được gọi là vectơ chỉ phương của đường thẳng \[\Delta \] nếu \[\vec{u}\ne \vec{0}\] và giá của \[{\vec{u}}\] song song hoặc trùng với \[\Delta \]
Nhận xét :
– Nếu \[{\vec{u}}\] là một vectơ chỉ phương của đường thẳng \[\Delta \] thì \[k\vec{u}(k\ne 0)\] cũng là một vectơ chỉ phương của \[\Delta \] , do đó một đường thẳng có vô số vectơ chỉ phương.
– Một đường thẳng hoàn toàn được xác định nếu biết môt điểm và một vectơ chỉ phương của đường thẳng đó.
2. Phương trình tham số của đường thẳng
– Phương trình tham số của đường thẳng \[\Delta \] đi qua điểm \[{{M}_{0}}({{x}_{0}};{{y}_{0}})\] và nhận vectơ \[\vec{u}=({{u}_{1}};{{u}_{2}})\] làm vectơ chỉ phương là :
\[\Delta :\left\{ \begin{matrix}x={{x}_{0}}+t{{u}_{1}} \\y={{y}_{0}}+t{{u}_{2}} \\\end{matrix} \right.\]
-Khi hệ số \[{{u}_{1}}\ne 0\] thì tỉ số \[k=\frac{{{u}_{1}}}{{{u}_{2}}}\] được gọi là hệ số góc của đường thẳng.
Từ đây, ta có phương trình đường thẳng \[\Delta \] đi qua điểm \[{{M}_{0}}({{x}_{0}};{{y}_{0}})\] và có hệ số góc k là:
\[y{{y}_{0}}=k(x{{x}_{0}})\]
Chú ý:
Ta đã biết hệ số góc \[k=tan\alpha \] với góc \[\alpha \] là góc của đường thẳng \[\Delta \] hợp với chiều dương của trục \[Ox\]
3. Vectơ pháp tuyến của đường thẳng
Định nghĩa: Vectơ \[{\vec{n}}\] được gọi là vec tơ pháp tuyến của đường thẳng \[\Delta \] nếu \[\vec{n}\ne \vec{0}\] và \[{\vec{n}}\] vuông góc với vectơ chỉ phương của \[\Delta \].
Nhận xét:
– Nếu \[{\vec{n}}\] là một vectơ pháp tuyến của đường thẳng \[\Delta \] thì \[k\vec{n}(k\ne 0)\] cũng là một vectơ pháp tuyến của \[\Delta \], do đó một đường thẳng có vô số vec tơ pháp tuyến.
– Một đường thẳng được hoàn toàn xác định nếu biết một và một vectơ pháp tuyến của nó.
4. Phương trình đường thẳng lớp 10 (dạng tổng quát)
Định nghĩa: Phương trình \[ax+by+c=0\] với \[a\] và \[b\] không đồng thời bằng \[0\], được gọi là phương trinh tổng quát của đường thẳng.
Trường hợp đặc biết:
+ Nếu \[a=0=>y=-\frac{c}{b};\Delta //Ox\]
+ Nếu \[b=0=>x=-\frac{c}{b};\Delta //Oy\]
+ Nếu \[c=0=>ax+by=0=>\Delta \] đi qua gốc tọa độ
+ Nếu \[\Delta \] cắt \[Ox\] tại \[(a;0)\] và \[Oy\] tại \[B(0;b)\] thì ta có phương trình đường thẳng \[\Delta \] theo đoạn chắn:
\[\frac{x}{a}+\frac{y}{b}=1\]
5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng \[{{\Delta }_{1}}\] và \[{{\Delta }_{2}}\]
có phương trình tổng quát lần lượt là :
\[a{{x}_{1}}+b{{y}_{1}}+{{c}_{1}}=0\]và \[a{{x}_{2}}+b{{y}_{2}}+{{c}_{2}}=0\]
Điểm \[{{M}_{0}}({{x}_{0}};{{y}_{0}})\] là điểm chung của ∆1 và ∆2 khi và chỉ khi \[({{x}_{0}};{{y}_{0}})\] là nghiệm của hệ hai phương trình:
\[(1)\left\{ \begin{matrix}a{{x}_{1}}+b{{y}_{1}}+{{c}_{1}}=0 \\a{{x}_{2}}+b{{y}_{2}}+{{c}_{2}}=0 \\\end{matrix} \right.\]
Ta có các trường hợp sau:
a) Hệ (1) có một nghiệm: ∆1 cắt ∆2
b) Hệ (1) vô nghiệm: ∆1 // ∆2
c) Hệ (1) có vô số nghiệm: ∆1 = ∆2
6.Góc giữa hai đường thẳng
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành 4 góc. Nếu ∆1 không vuông góc với ∆2thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng ∆1 và ∆2. Nếu ∆1 vuông góc với ∆2 thì ta nói góc giữa ∆1 và ∆2bằng 900 .Trường hợp ∆1 và ∆2 song song hoặc trùng nhau thì ta quy ước góc giữa ∆1 và ∆2 bằng\[{{0}^{0}}.\]. Như vậy gương giữa hai đường thẳng luôn bé hơn hoặc bằng \[{{90}^{0\text{ }~}}\].
Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là \[\widehat{{{\Delta }_{1}},{{\Delta }_{2}}}\]
Cho hai đường thẳng ∆1 = a1x+b1y + c1 = 0
∆2 = a 2+ b2y +c2 = 00
Đặt \[\varphi =\widehat{{{\Delta }_{1}},{{\Delta }_{2}}}\]
\[\cos \varphi =\frac{\left| {{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{a_{2}^{2}+b_{2}^{2}}}\]
Chú ý:
+ \[\Delta 1\bot \Delta 2\Leftrightarrow {{n}_{1}}\bot {{n}_{2}}\Leftrightarrow {{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}=0\]
+ Nếu \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}\] và \[{{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\] có phương trình y = k1 x + m1 và y = k2 x + m2 thì
\[{{\Delta }_{1}}\bot {{\Delta }_{2}}\Leftrightarrow {{k}_{1}}.{{k}_{2}}=-1\]
7.Công thức tính khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng \[Oxy\] cho đường thẳng \[\Delta \] có phương trình \[ax+by+c=0\] và điểm\[{{M}_{0}}({{x}_{0}};{{y}_{0}})\].Khoảng cách từ điểm \[{{M}_{0}}\] đến đường thẳng \[\Delta \] kí hiệu là \[({{M}_{0}},\Delta )\], được tính bởi công thức
\[d({{M}_{0}},\Delta )=\frac{|a{{x}_{0}}+b{{y}_{0}}+c|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
=> Vậy là chúng ta đã tìm hiểu xong các vấn đề xoay quanh về phương trình đường thẳng lớp 10. Để chinh phục chuyên đề này, chúng tôi có cung cấp cho các em khá nhiều tài liệu học tập. Link bài tập được đặt ở phần 9 – Bài tập vận dụng.
8. **BÀI TẬP VẬN DỤNG**
Bài tập chuyên đề phương trình đường thẳng Oxy: CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆU
LỜI KẾT
Trên đây là toàn bộ các nội dung về chủ đề phương trình đường thẳng lớp 10. Mong rằng sẽ giúp các em chinh phục một phần nào chuyên đề này. Để xem thêm nhiều tài liệu hay hơn nữa về chuyên đề phương trình đường thẳng lớp 10, các em chọn các mục ở cuối bài viết này để xem chi tiết hơn.




 056.3753648
056.3753648
 Chat FB
Chat FB