Tóm tắt tài liệu
Các phép toán trên tập hợp bao gồm khá nhiều dạng với một số biến thể khác nhau như: xác định tập hợp và phép toán trên tập hợp và sử dụng biểu đồ ven để giải toán. Những dạng này nhằm giúp có một nguồn tài liệu tư học phong phú, đầy đủ và rõ ràng. Chúng tôi đã tập hợp một số các phép toán trên tập hợp có lời giải chi tiết. Những bài tập dưới đây mang tính cốt lõi, đặc trưng nhất cho từng các dạng toán. Do đó, đây được coi là những bài tập cơ sở giúp phát triển tư duy về các phép toán của các em.














Lý thuyết về các phép toán tập hợp
Tập hợp là gì?
Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa. Cách xác định tập hợp: Liệt kê phân tử: viết các phần tử của tập hợp trong hai dấu móc {……}. Chỉ ra tính chất đăc trưng cho các phần tử của tập hợp.
- Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu.
- Tập hợp con – Tập hợp bằng nhau
Các phép toán trên tập hợp
- Giao của hai tập hợp
- Hợp của hai tập hợp
- Hiệu của hai tập hợp
Các tập hợp được cho dưới nhiều dạng như: Đoạn, khoảng, nửa khoảng, nửa đoạn,…
Dạng toán 1: Xác định tập hợp và các phép toán trên tập hợp
Ví dụ 1: Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng
A. 0 ; 1; 2; 3; 4
B. 0 ; 4; 8; 12;16
C. 1;2;4;8;16
Dạng toán 2: Sử dụng biểu đồ ven để giải toán tập hợp
Phương pháp:
- Chuyển bài toán về ngôn ngữ tập hợp
- Sử dụng biểu đồ ven để minh họa các tập hợp
- Dựa vào biểu đồ ven ta thiết lập được đẳng thức (hoặc phương trình hệ phương trình) từ đó tìm được kết quả bài toán
- Trong dạng toán này ta kí hiệu n. X là số phần tử của tập X .
Ví dụ 1: Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em
biết chơi cầu lông, 15 em biết chơi cả hai. Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? Bao nhiêu em chỉ biết
đánh cầu lông? Sĩ số lớp là bao nhiêu?
Lời giải:
Dựa vào biểu đồ ven ta suy ra số học sinh chỉ biết đá cầu là 25 – 15 =10.
Số học sinh chỉ biết đánh cầu lông là: 30 – 15 =15
Do đó ta có sĩ số học sinh của lớp 10A1 là: 10+15+15 = 40
Trong số 220 học sinh khối 10 có 163 bạn biết chơi bóng chuyền, 175 bạn biết chơi bóng bàn còn 24 bạn không biết
chơi môn bóng nào cả. Tìm số học sinh biết chơi cả 2 môn bóng.
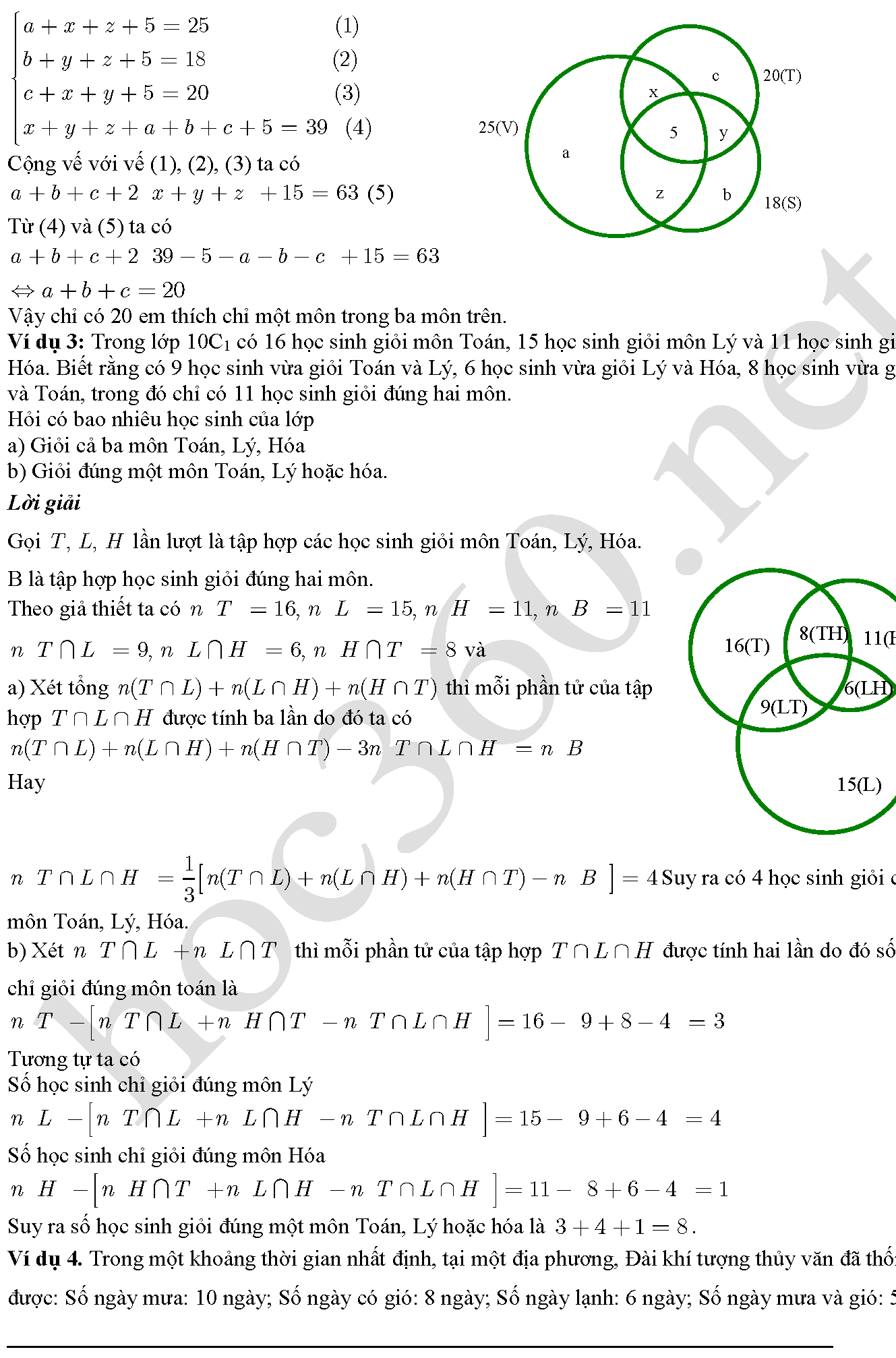
Ví dụ 2: Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn
Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên?
Lời giải:
Gọi a,b,c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
- x là số học sịnh chỉ thích hai môn là văn và toán
- y là số học sịnh chỉ thích hai môn là Sử và toán
- z là số học sịnh chỉ thích hai môn là văn và Sử
Ta có số em thích ít nhất một môn là 45 – 6 = 39. Dựa vào biểu đồ ven ta có hệ phương trình. Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
Dạng toán 3: Chứng minh tập hợp bằng nhau, các quan hệ giữa các tập hợp
Các dạng đề bài của phần này gồm:
- Cho các tập hợp, chứng minh mối quan hệ giữa các tập hợp
- Chứng minh A là con B
- Chứng minh A thuộc B
- Chứng minh A giao B bằng rỗng
Dạng toán 4: Các phép toán trên tập hợp con
Phương pháp:
Để tìm A giao B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp A, B lên trục số
- Biểu diễn các tập A, B trên trục số(phần nào không thuộc các tập đó thì gạch bỏ)
- Phần không bị gạch bỏ chính là giao của hai tập hợp A, B
Để tìm A hợp B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp A, B lên trục số
- Tô đậm các tập A, B trên trục số
- Phần tô đậm chính là hợp của hai tập hợp A, B
Để tìm A \ B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp A, B lên trục số
- Biểu diễn tập A trên trục số(gạch bỏ phần không thuộc tập A ), gạch bỏ phần thuộc tập B trên trục số
- Phần không bị gạch bỏ chính là A \ B
Ví dụ 1: Cho tập A = [-1; 2), B = (-3; 1) và C = (1; 4].
a) Viết tập A, B, C dưới dạng chỉ ra tính chất đặc trưng của các phần tử và biểu diễn chúng trên trục số.
b) Xác định các phép toán A B, B C, A \ B.
Những bài toán trên sẽ giúp các bạn biết thêm về các mẫu bài toán hay về các phép toán trên tập hợp. Những bài toán này cũng giúp các bạn ôn lại những kiến thức mà các bạn đã quên trong quá trình hoc. Hơn thế nữa, các bài toán này còn giúp bạn cũng cố lại tư duy học toán một cách logic, từ từ. Hỗ trợ được việc nhớ trước quên sau nhé.
Bạn có thể tìm thấy tài liệu này thông qua những từng khóa nào?
- các phép toán trên tập hợp số tự nhiên
- kí hiệu tập hợp con
- lý thuyết tập hợp và các phép toán trên tập hợp
- ví dụ về các phép toán trên tập hợp
- cách tính tập hợp các phép toán tập hợp
- toán cao cấp
- toán rời rạc
- chương tập hợp các kí hiệu toán học lop 7
Tham khảo
1. https://www.youtube.com/watch?v=Qk9lCXtu8jw
2. https://vi.wikipedia.org/wiki/T%E1%BA%ADp_h%E1%BB%A3p_con_(to%C3%A1n_h%E1%BB%8Dc)
Video Học Tập
(Lý thuyết các phép toán trên tập hợp)




 056.3753648
056.3753648
 Chat FB
Chat FB