Lý thuyết hàm số lớp 10

Hàm số lớp 10 là một trong những chuyên đề quan trọng nhất trong chương trình toán lớp 10. Mảng kiến thức hàm số sẽ được đề cập lại vào năm lớp 12. Những câu hỏi về hàm số chiếm 1 tỉ lệ khá quan trọng trong bài thi THPT QG.

Ở bài viết này, chúng ta sẽ tìm hiểu những khái niệm sơ khai nhất về hàm số (đặc biệt trong chương trình hàm số lớp 10). Chủ đạo là các hàm số: hàm số bậc nhất, hàm số bậc hai và các vấn đề liên quan như: đồ thị hàm số, khảo sát hàm số.

Hãy cùng đọc và nghiên cứu kĩ lưỡng nhé ^ ^

1) Định nghĩa hàm số

Cho \[D\in R,D\ne \phi \]. Một hàm số xác định trên \[D\] là một quy tắc \[f\] cho tương ứng mỗi số \[x\in D\] với một và duy nhất chỉ một số \[y\in R\]. Ta kí hiệu:

\[f:D\to R\]

\[x\to y=f(x)\]

Tập hợp \[D\] được gọi là tập xác định ( hay miền xác định) \[x\] được gọi là biến số (hay đối số), \[{{y}_{0}}=f({{x}_{0}})\] tại \[x={{x}_{0}}\].

Một hàm số có thể được cho bằng một công thức hay bằng biểu đồ hay bằng bảng.

Lưu ý rằng, khi cho nột hàm số bằng công thức mà không nói rõ tập xác định thì ta ngầm hiểu tập xác định \[D\] là tập hợp các số \[x\in R\] mà các phép toán trong công thức có nghĩa.

2. Đồ thị hàm số

Đồ thị của hàm số:

    \[f:D\to R\]

   \[x\to y=f(x)\]

là tập hợp các điểm \[(x;f(x)),x\in D\] trên mặt phẳng tọa độ.

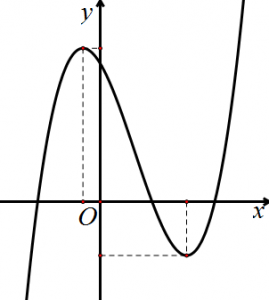
Ví dụ về đồ thị hàm số bậc 3

3. Sự biến thiên của hàm số trên R

Hàm số \[y=f(x)\] là đồng biến trên khoảng \[(a;b)\] nếu với mọi \[{{x}_{1}},{{x}_{2}}\in (a;b)\] mà \[{{x}_{1}}<{{x}_{2}}\Leftrightarrow f({{x}_{1}})<f({{x}_{2}})\] hay \[{{x}_{1}}\ne {{x}_{2}}\] ta có \[\frac{f({{x}_{1}})-f({{x}_{2}})}{{{x}_{1}}-{{x}_{2}}}>0\].

Hàm số \[y=f(x)\] là nghịch biến trên khoảng \[(a;b)\] nếu với mọi \[{{x}_{1}},{{x}_{2}}\in (a;b)\] mà \[{{x}_{1}}<{{x}_{2}}\Rightarrow f({{x}_{1}})>f({{x}_{2}})\] hay \[{{x}_{1}}\ne {{x}_{2}}\] ta có \[\frac{f(x1)-f(x2)}{{{x}_{1}}-{{x}_{2}}}<0\].

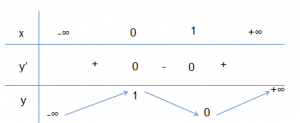
Ví dụ sự biến thiên của hàm số

4. Tính chẵn lẻ của các hàm số lớp 10

Hàm số \[f:D\to R\]

\[x\to y=f(x)\] được gọi là hàm số chẵn nếu: \[x\in D\Rightarrow -x\in D\] và \[f(-x)=f(x)\], là hàm số lẻ nếu \[x\in D\Rightarrow -x\in D\] và \[f(-x)=-f(x)\].

Đồ thị của hàm số chẵn có trục đối xứng là trục tung. Đồ thị của hàm số lẻ nhận gốc O của hệ trục tọa độ làm tâm đối xứng.

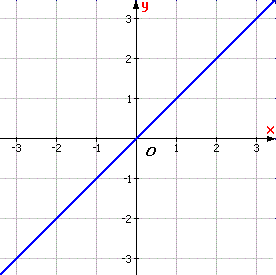
Đồ thị hàm số lẻ đối xứng qua O

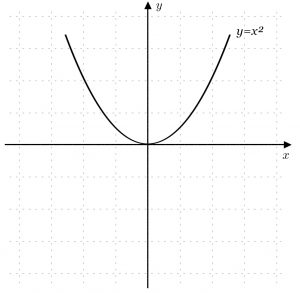
Đồ thị hàm số chẵn đối xứng qua trục tung Oy

Vậy là chúng ta vừa tìm hiểu xong kiến thức về hàm số lớp 10. Các kiến thức do tailieure.com biên soạn một cách chi tiết rõ ràng và thống nhất. Bất cứ lỗi sai nào được phát hiện mong các em bình luận xuống phía cuối bài viết (đăng nhập facebook để bình luận). Chúc các em học tốt!

Xem thêm video

video trên Thầy Linh dạy toán

video trên Trung tâm giáo dục Tam Nguyên

• Chuyên mục: Hàm số bậc nhất và hàm số bậc hai