Tóm tắt tài liệu
Hàm số bậc 3 là một chủ đề khá quan trọng, thường xuất hiện trên đề thi là những câu hỏi cơ bản và cả những câu rất phức tạp. Do đó, để làm tốt dạng toán khảo sát hàm số trong đề thi, các em cần nắm vững cách khảo sát và vẽ đồ thì hàm số bậc 3 và thực hiện chúng nhanh nhất có thể. Bài viết hôm nay gồm 2 phần: Phương pháp khảo sát, vẽ đồ thị và bài tập ứng dụng.
A. Các bước khảo sát và vẽ đồ thị hàm số bậc 3
\[y=a.{{x}^{3}}+b.{{x}^{2}}+c.x+d\], \[a\ne 0\]
Bước 1: Tìm tập xác định của hàm số \[D=R\]
Bước 2: Tính đạo hàm của hám số
\[{y}’=3a.{{x}^{2}}+2b.x+c\], Suy ra \[{\Delta }’={{b}^{2}}-3ac\]
+) Nếu \[{\Delta }’>0\] thì hàm số có 2 cực trị
+) Nếu \[{\Delta }’\le 0\] thì hàm số luôn tăng hoặc luôn giảm trên \[R\] tức hàm số không có cực trị
Bước 3: Tính đạo hàm cấp 2
Ta tính được: \[{y}”=6a.x+2b\]
Khi đó nghiệm của \[{y}”=0\] là hoành độ điểm uốn của đồ thị. ( Đồ thị nhận điểm uống làm tâm đối xứng )
Bước 4: Suy luận ra các giới hạn theo từng trường hợp của a.
+) Nếu \[a>0\] thì \[\underset{x\to -\infty }{\mathop{\lim }}\,y=-\infty ,\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty \] (Đồng biến)
+) Nếu \[a<0\] thì \[\underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty ,\underset{x\to +\infty }{\mathop{\lim }}\,y=-\infty \] (Nghịch biến)
Từ các suy luận trên ta dễ dàng vẽ được bảng biến thiên như sau:
Bước 5: Vẽ bảng biến thiên tùy trường hợp (theo dấu của a)
Trường hợp 1: \[a>0\]
+) \[{\Delta }’>0\], Hàm số có 2 cực trị
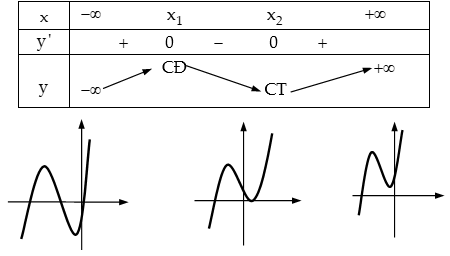
+) \[{\Delta }’\le 0\], suy ra \[{y}’\ge 0\] \[\forall x\in R\]. Hàm số luôn tăng trên \[R\]
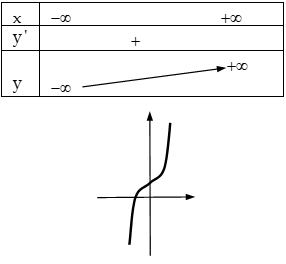
Trường hợp 2: \[a<0\]
+) \[{\Delta }’>0\], hàm số có 2 cực trị
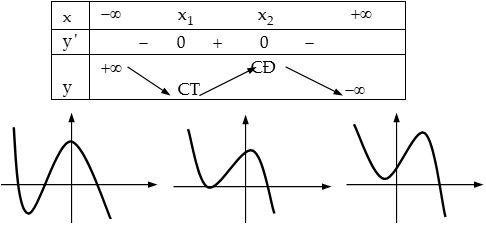
+) \[{\Delta }’\le 0,{y}’\le 0,\forall x\in R\], Hàm số luôn giảm trên \[R\]
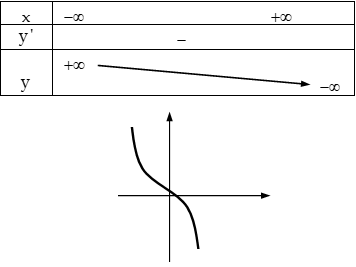
Một số tính chất được suy ra từ hàm số bậc 3 khi khảo sát và vẽ đồ thị:

B. Bài tập khảo sát hàm số HAY – LẠ -KHÓ (Trần Sĩ Tùng)
Bài viết hôm nay có lẽ đã giải quyết một phần nào cho các đọc giả còn thiếu kiến thức về phần khảo sát và vẽ đồ thị hàm số bậc 3. Để vận dụng linh hoạt lý thuyết vào bài tập, các em học sinh đặc biệt phải thực hành thật nhiều bài tập mà tailieure.com cung cấp sau mỗi bài học.



 056.3753648
056.3753648
 Chat FB
Chat FB