Tóm tắt tài liệu
Dưới đây là các dạng bất phương trình vô tỉ và hướng dẫn phương pháp, cách giải các bất phương trình vô tỉ đó. Nhằm cung cấp cho các em những phương pháp mạnh nhất để giải quyết những bài toán này, chúng tôi tổng hợp được tài liệu với những phương pháp cực hay được giới thiệu ngay bên dưới bài viết này. Hãy cùng chúng tôi xem qua các phương pháp bằng cách tải tài liệu xuống nhé!
Kĩ thuật xử lý bất phương trình vô tỉ
- Phương pháp biến đổi tương đương
- Kĩ thuật chia điều kiện
- Kĩ thuật khai căn
- Kĩ thuật phân tích thành nhân tử
- Kĩ thuật nhân chia liên hợp
- Kĩ thuật đặt ẩn phụ – Đặt ẩn phụ lượng giác
- Kĩ thuật đánh giá trong bất phương trình
- Kĩ thuật sử dụng tích vô hướng của véc tơ để giải bất phương trình
- Kĩ thuật khảo sát hàm số để đánh giá bất phương trình vô tỉ
- Kĩ thuật sử dụng tính đối xứng của hai nghiệm
Phương pháp biến đổi tương đương giải bất phương trình
Hai bất phương trình được gọi tương đương khi chúng có cùng tập nghiệm. Cộng trừ hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình. Nhân chia hai vế của bất phương trình với cùng một biểu thức luôn dương hoặc âm mà không làm thay đổi điều kiện của bất phương trình. Lũy thừa bậc lẻ hai vế, khai căn bậc lẻ hai vế của một bất phương trình. Lũy thừa bậc chẵn hai vế, khai căn bậc chẵn hai vế khi hai vế của bất phương trình cùng dương. Nghịch đảo hai vế của bất phương trình khi hai vế cùng dương ta phải đổi chiều.
Kỹ thuật lũy thừa hai vế
Ở kĩ thuật này, đặc biệt chú ý tới điều kiện của bài toán. Nếu điều kiện đơn giản có thể kết hợp vào bất phương trình, còn điều kiện phức tạp nên để riêng.

Xem thêm: Giải bất phương trình bằng máy tính
Kỹ thuật khai căn
Biến đổi các biểu thức trong căn thức thành hằng đẳng thức.
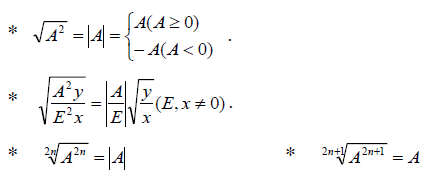
Kỹ thuật phân tích thành nhân tử đưa về bất phương trình tích
Đây là kỹ thuật giải đòi hỏi có tư duy cao, kỹ năng phân tích thành nhân tử thành thạo, cần phải nhìn ra nhân tử chung nhanh.
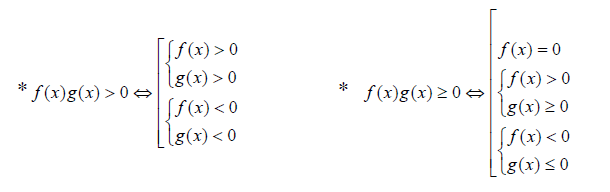
Kỹ thuật nhân chia liên hợp
- Nên nhẩm với một số nghiệm nguyên đơn giản.
- Chú ý tới các biểu thức nhân chia liên hợp.
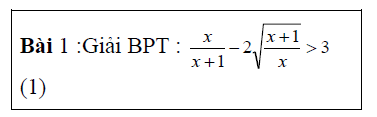
Phương pháp đặt ẩn phụ
Một số yêu cầu là: Dạng này học sinh cần nhớ cách đặt ẩn và từ đó mở rộng cho bài toán tương tự chú ý tới các điều kiện của ẩn.

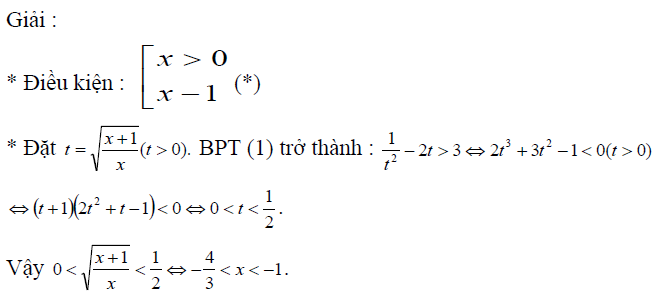
Phương pháp đánh giá bằng bất đẳng thức
– Nhớ được cách xét tính đơn điệu của một hàm số, lập bảng biến thiên…
– Nhớ các bất đẳng thức.
– Thường áp dụng cho các Bài toán bất phương trình vô tỉ đặc thù, phức tạp không có thuật toán cụ thể nhưng
hay có trong các kì thi đại học các năm gần đây. Hai bất đẳng thức cơ bản nhất là:
- Bất đẳng thức Côsi
- Bất đẳng thức Bunhiacopski
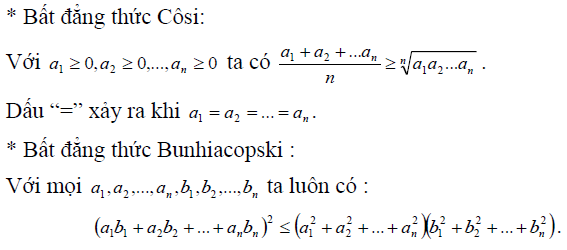
Kỹ thuật sử dụng tích vô hướng của hai véc tơ trong bất phương trình
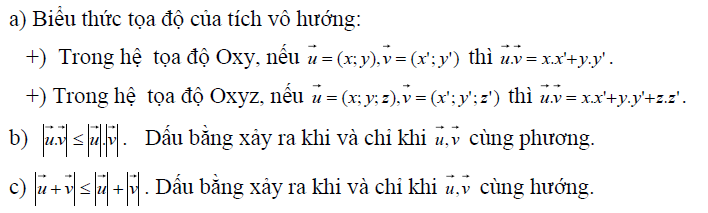
Kỹ thuật khảo sát hàm số để đánh giá bất phương trình
Để giải bất phương trình ta khảo sát hoặc căn cứ vào tính chất của các hàm số đưa ra bảng biến thiên và từ
bảng biến thiên đưa ra kết luận.
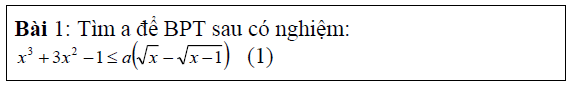
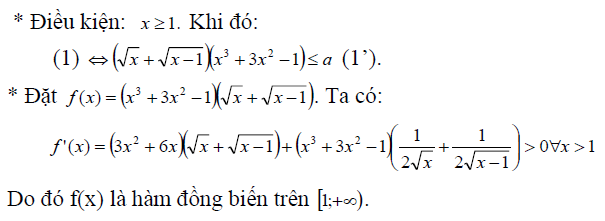
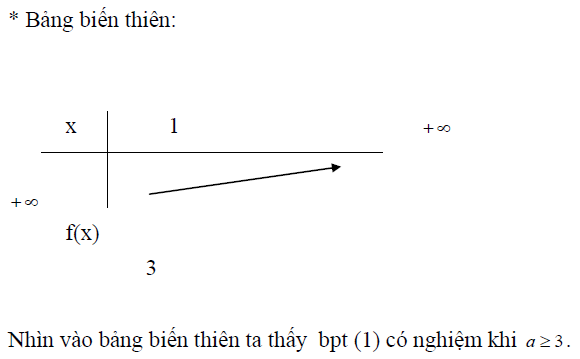
Kỹ thuật sử dụng tính đối xứng của hai nghiệm
Đây là cách đánh giá bất phương trình vô tỉ khá thông minh, các cách làm được dựa vào kinh nghiệm của người giải bài tập. Dựa vào mức độ va chạm với các loại bài tập đó.
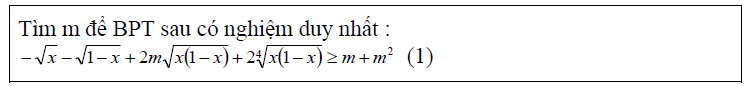
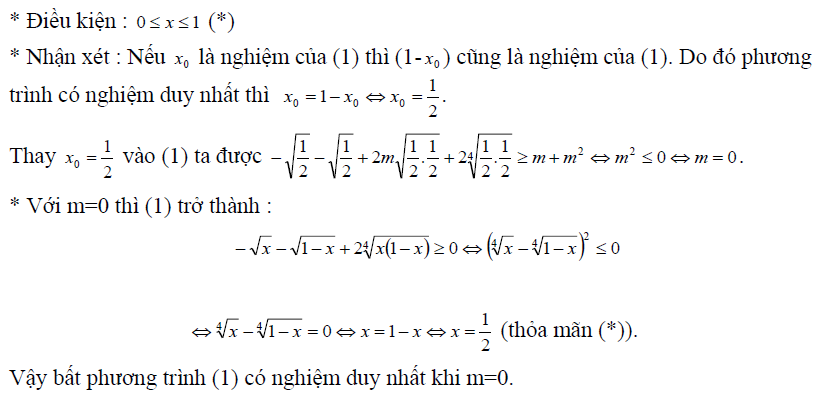
Tổng hợp các bài tập giải bất phương trình trong tài liệu
Dưới đây là một số bài tập giải bất phương trình vô tỉ có chọn lọc từ nhiều nguồn. Để xem đầy đủ lời giải cũng như đề bài tất cả, bạn đọc có thể tải file về và in ra nếu cần thiết. Ngoài ra vẫn còn một số bài tập không có lời giải, bài tập đề nghị. Các bạn có thể trao đổi ở ngay dưới tài liệu này!
![]()
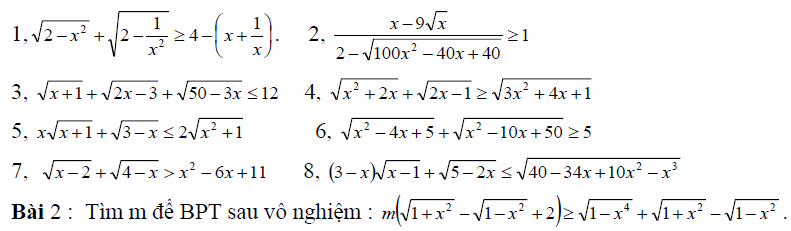

Vậy là chúng ta vừa tham khảo xong 10 phương pháp giải bất phương trình vô tỉ cơ bản nhất, phổ biến nhất. Các phương pháp trên không chỉ giúp chúng ta giải các bài tập cơ bản mà còn một số bài tập trong các đề thi HSG nếu biết cách khai thác.
Xem thêm: Cách giải bất phương trình lượng giác




 056.3753648
056.3753648
 Chat FB
Chat FB