Tóm tắt tài liệu
Dưới đây là tổng hợp những dạng toán đặc trưng nhất về tìm GTLN GTNN của hàm số lớp 10. Mỗi dạng bài được đề cập đều có 2 phần: phương pháp giải và bài tập ứng dụng. Như các em đã biết, hàm số chiếm một vai trò không hề nhỏ trong đề thi, đặc biệt là chương trình toán THPT. Hầu hết các đề thi đều chứa câu hỏi loại này. Một trong những dạng toán các em học sinh lo ngại nhất vẫn là các bài toán cực trị. Bởi tính phong phú, cũng như cách giải quyết khá phức tạp. Hôm nay tài liệu rẻ đăng tải 58 trang tài liệu này để đóng góp những phương pháp tìm cực trị hàm số hay nhất cho các em học sinh.
A. TÓM TẮT LÝ THUYẾT VỀ GIÁ TRỊ NHỎ NHẤT – GIÁ TRỊ LỚN NHẤT
Chắc hẳn các em đã biết cách tìm giá trị lớn nhất của phương trình bậc 2, một dạng toán thường gặp ở học sinh THCS. Tuy nhiên, trước khi tiến vào các dạng bài về GTLN – GTNN của hàm số, chúng ta cần điểm qua một số vấn đề lý thuyết để hiểu rõ hơn bản chất, từ có đó phương hướng hơn khi gặp các bài tập loại này.



B. CÁC DẠNG TOÁN TÌM GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Dạng 1: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn
Đây là một dạng toán khá quen thuộc. Không phải tất cả hàm số đều đạt giá trị cực trị trên tập xác định của nó. Một số hàm số luôn tiến về vô cùng khi giá trị biến chạy đến vô cùng. Do đó, để xuất hiện giá trị lớn nhất, nhỏ nhất của hàm số, người ta đã chặn hai đầu của hàm số. Bằng cách giới hạn chúng trên một đoạn bất kì thuộc tập xác định.

Vừa rồi là phương pháp chung để thực hiện các dạng toán này tốt hơn, ta cùng đến với 2 ví dụ mẫu sau:

Dạng 2: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng
Tương tự như dạng một là hàm số đã bị giới hạn nhỏ hơn trong tập xác định. Tuy nhiên, cái khó của dạng này là đáp án rất khác thường. Có những hàm số tồn tại GTNN, GTLN trên TXĐ của chúng nhưng trên khoảng đầu bài cho thì lại không. Nếu chưa gặp dạng bài này, có thể nhiều bạn học sinh sẽ bị đánh lừa. Chúng ta cùng tìm hiểu sơ qua phương pháp của dạng bài tập này:

Sau đây là ví dụ đặc trưng của dạng toán này. Các em cần nắm rõ từng ví dụ trước khi tìm hiểu sâu hơn vào các biến thể mà dạng toán này mang lại:


Dạng 3: Ứng dụng GTLN, GTNN vào giải toán thực tế
Trong những năm gần đây, toán học đã dần chuyển sang hình thức thi trắc nghiệm. Các bài toán thực tế được cho là một chủ đề lạ, chủ đề khó, bởi lẽ các bài toán đưa ra đều không có qui tắc, hướng làm cụ thể như toán tự luận. Học sinh chỉ có thể phân dạng chúng theo các nhóm kiến thức đã học. Một dạng toán thực tế xuất hiện khá nhiều, có thể là nhiều nhất, đó là ứng dụng hàm số tìm min max để giải quyết các vấn đề thực tiễn. Hãy cùng tìm hiểu các ví dụ sau:

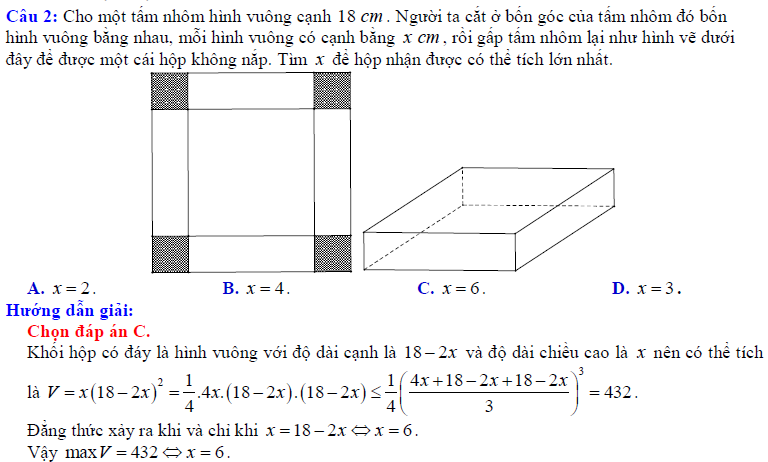
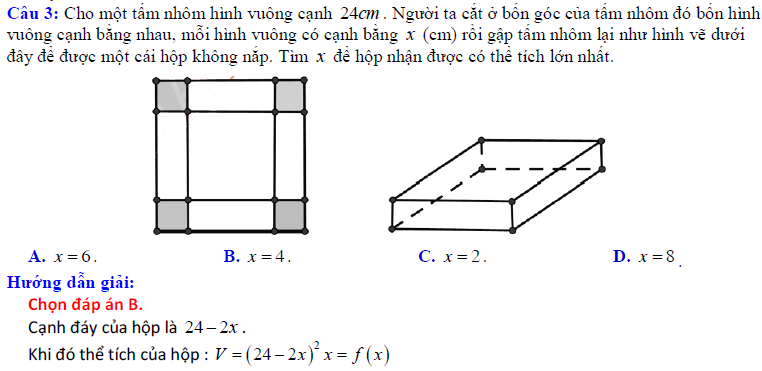

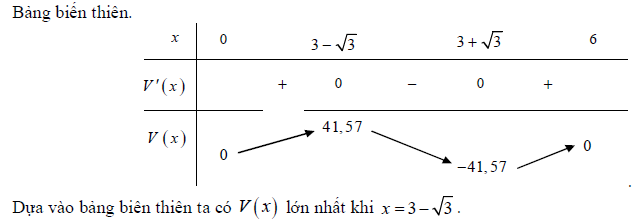
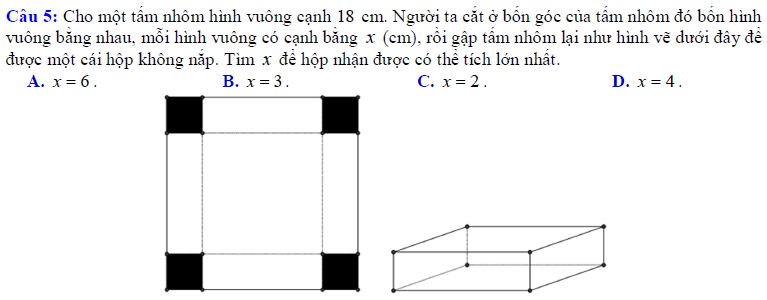

Vậy là chúng ta vừa tìm hiểu xong 3 dạng toán tìm gtln gtnn của hàm số lớp 10. Để đạt kết quả cao nhất trong khi rèn luyện, các em có thể tải tài liệu trên, sau đó in ra và rèn luyện hằng ngày. Tài liệu trên là một tâm huyết của đội ngũ admin tài liệu rẻ, mong rằng sẽ giúp ích một phần nào đó cho các em học sinh. Chúc các em học tốt, và nhớ hãy xem thêm nhiều tài liệu khác trên tailieure.com nhé.
Xem thêm video
- Từ khóa: tìm giá trị lớn nhất nhỏ nhất của hàm số chứa căn, tìm a để giá trị lớn nhất của hàm số trên đoạn đạt giá trị nhỏ nhất, tìm gtln gtnn của hàm số lượng giác lớp 11 nâng cao.
- Chuyên mục: Hàm số bậc nhất và hàm số bậc hai




 056.3753648
056.3753648
 Chat FB
Chat FB