Tóm tắt tài liệu
Số phức được sử dụng trong nhiều lĩnh vực khoa học, như khoa học kỹ thuật, điện từ học, cơ học lượng tử, toán học ứng dụng chẳng hạn như trong lý thuyết hỗn độn.Đặc biệt, số phức cũng là một trong những câu hỏi xuất hiện trong đề thi THPTQG. Để hiểu rõ hơn về số phức, chúng tôi đã tổng hợp nên tài liệu lý thuyết số phức vô cùng chi tiết, đầy đủ tất cả các vấn đề liên quan đến số phức.
Khái niệm số phức
Tập hợp số phức: C
Số phức ( dạng đại số ) : z=a+bi.
(a, b thuộc R, a là phần thực, b là phần ảo, i là đơn vị ảo, i2=-1)
Biểu diễn hình học của số phức
Số phức z=a+bi (a, b thuộc R) được biểu diễn bởi điểm M(a; b) hay bởi u = (a; b) trong mp (Oxy) (mp thức)
Cộng và trừ số phức
(a+bi)+(c+di)=(a+c)+(b+d)i;
(a+bi)−(c+di)=(a−c)+(b−d)i;
Số đối của z = a + bi là -z = -a – bi.
Nhân hai số phức
(a+bi)(c+di)=(ac−bd)+(ad+bc)i
Một số điểm lý thuyết số phức quan trọng khác
- Số phức liên hợp
- Môđun của số phức
- Chia hai số phức
- Căn bậc hai của số phức
- Phương trình bậc hai Az2+Bz+C=0. (*)
- Dạng lượng giác của số phức
- Nhân chia số phức dưới dạng lượng giác
- Công thức Moa-vrơ
- Căn bậc hai của số phức dưới dạng lượng giác
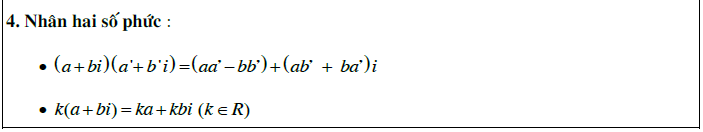
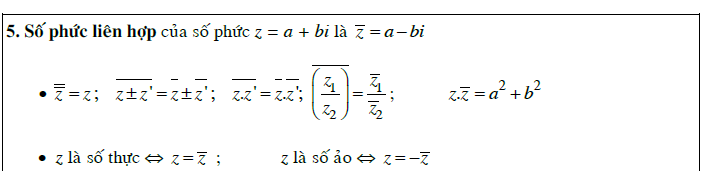
Vậy là chúng ta đã cùng nhau đọc xong tài liệu lý thuyết số phức và nhận ra nhiều điều thú vị về số phức,ccũng như trang bị đầy đủ kiến thức để làm được tất cả các dạng bài tập liên quan đến số phức. Hãy in tài liệu này ra, lúc cần thì đọc lại, hãy học thuộc những kiến thức lý thuyết, vì toán phải nhớ lý thuyết thì mới có thể làm bài được. Cảm ơn các bạn đã đọc, chúc các bạn học tốt!
