Tóm tắt tài liệu
Hoán vị chỉnh hợp tổ hợp là chuyên đề nền tảng nhất khi học tổ hợp xác suất. Nó tiếp nối các qui tắc đếm mà chúng ta đã được tìm hiểu ở bài trước. Tài liệu này cung cấp cho các em đầy đủ các điểm lý thuyết cũng như các dạng bài tập liên quan đến hoán vị, chỉnh hợp và tổ hợp. Cấu trúc tài liệu được phân chia như sau
Phần 1: Tổng quan lý thuyết
- Hai qui tắc đếm
- Hoán vị
- Chỉnh hợp
- Tổ hợp
Phần 2: Các dạng toán ôn thi thpt quốc gia
- Dạng 1: Các dạng toán chọn vật, chọn người
- Dạng 2: Các bài toán lập số chọn số
- Dạng 3: Các bài toán liên quan đến phép đếm trong hình học
- Dạng 4: Các bài toán về phân chia trong tập hợp
PHẦN 1: KIẾN THỨC CƠ BẢN
BÀI HỌC 1: HAI QUY TẮC ĐẾM
1. Quy tắc cộng:
Giả sử một công việc có thể thực hiện theo phương án A HOẶC phương án B.
Trong đó: Phương án A có m cách thực hiện. Phương án B có n cách thực hiện.
Vậy số cách để thực hiện công việc là m + n (cách)
VD1: Trong một cuộc thi, Ban tổ chức công bố danh sách các đề tài : 7 đề tài về thiên nhiên; 8 đề tài về lịch
sử; 10 đề tài về con người; 6 đề tài về văn hóa. Hỏi có bao nhiêu cách chọn đề tài ?
(ĐS: có 7 + 8 + 10 + 6 = 31 cách chọn)
VD2: An cần mua 1 áo sơ mi cỡ 39 hoặc 40. Trong đó cỡ 39 có 5 màu khác nhau, cỡ 40 có 4 màu khác nhau.
Hỏi An muốn mua 1 áo sơ mi thì có bao nhiêu cách chọn ?
(ĐS: An có 9 cách chọn)
VD3: Tại 1 trường học, có 41 học sinh chỉ giỏi văn; 22 học sinh chỉ giỏi toán. Nhà trường muốn cử một học
sinh giỏi đi dự trại hè toàn quốc. Vậy nhà trường có bao nhiêu cách chọn ?
(ĐS: Có 41 + 22 = 63 cách chọn)
2. Quy tắc nhân
Giả sử môt công việc nào đó bao gồm hai công đoạn A và B. Công đoạn A có n cách thực hiện và công đoạn
B có m cách thực hiện. khi đó công việc có thể được thực hiện bởi (n.m) cách.
VD1: Bạn An qua nhà Bình, rủ Bình qua nhà Cường đi chơi. Biết từ nhà An đến nhà Bình có 3 con đường đi
khác nhau. Từ nhà Bình qua nhà Cường có 4 con đường đi khác nhau. Hỏi bạn An muốn tới nhà Cường có
bao nhiêu cách chọn đường đi.
(ĐS: Có 3.4 = 12 cách)
VD2: Để làm nhãn cho một chiếc ghế, người ta quy ước nhãn gồm 2 phần: Phần thứ nhất là 1 chữ cái có
trong 24 chữ cái, phần thứ 2 là một số nguyên dương nhỏ hơn 26. Hỏi có bao nhiêu ghế được dán nhãn khác
nhau ?
(ĐS: Có 24.25 = 600 ghế được dán nhãn khác nhau)
3. Bài tập áp dụng
Phương pháp giải toán :
+ Xác định xem công việc được thực hiện theo phương án hay công đoạn (phân biệt phương án và công
đoạn).
+ Tìm số cách thực hiện A và B.
+ Áp dụng qui tắc cộng hay nhân.
Bài 1: An đến văn phòng phẩm mua quà tặng bạn. Trong cửa hàng có 3 mặt hàng: Bút, vở, thước. Bút có 5
loại, vở có 4 loại, thước có 3 loại. Hỏi An có bao nhiêu cách chọn quà gồm 1 bút, 1 vở và 1 thước ?
Hướng dẫn:
+ Có 5 cách chọn bút, ứng với 1 cách chọn bút có 4 cách chọn vở.
+ Ứng với mỗi cách chọn 1 bút, 1 vở có 3 cách chọn 1 thước.
Vậy có: 5.4.3 = 60 cách chọn
Bài 2: Từ các số tự nhiên, có thể lập được bao nhiêu tờ vé số mà mỗi vé số có 6 chữ số khác nhau ?
a có 10 cách chọn (được chọn cả chữ số 0 đứng đầu)
2 a có 9 cách chọn (do không chọn lại chữ số đã chọn trước đó)
3 a có 8 cách chọn (do không chọn lại chữ số đã chọn trước đó)
…
…
6 a có 5 cách chọn
Vậy tất cả có: 10.9.8.7.6.5 = 151.200 tờ vé số
Bài 3: Trong một trường THPT, khối 11 có : 160 học sinh tham gia câu lạc bộ toán, 140 học sinh tham gia
câu lạc bộ tin, 50 học sinh tham gia cả 2 câu lạc bộ. Hỏi khối 11 có bao nhiêu học sinh ?
Hướng dẫn:
Học sinh khối 12 là 160 +140 − 50 = 250 học sinh (Quy tắc cộng mở rộng)
Bài 4: Một lớp có 40 học sinh, đăng ký chơi ít nhất một trong hai môn thể thao bóng đá và cầu lông. Có 30
học sinh đăng ký bóng đá, 25 học sinh đăng ký cầu lông. Hỏi có bao nhiêu học sinh đăng ký cả 2 môn thể
thao ?
Hướng dẫn:
+ Goi x là số học sinh đăng ký cả 2 môn thể thao, ta có: 40 = 30 + 25 − x⇒ x = 15
Vậy có 15 học sinh đăng ký cả 2 môn thể thao
Bài 5: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải, nhựa). Hỏi có bao
nhiêu cách chọn một chiếc đồng hồ gồm 1 mặt và một dây ?
Hướng dẫn: Có 3.4 = 12 (cách)
Bài 6: Một người vào cửa hàng ăn, người đó muốn chọn thực đơn gồm một món ăn trong 10 món, một loại
hoa quả tráng miệng trong 5 loại hoa quả và một loại nước uống trong 4 loại nước uống. Hỏi có bao nhiêu
cách chọn thực đơn cho bữa ăn ?
Hướng dẫn:
+ Món ăn có: 10 cách chọn.
+ Ứng với cách chọn 1 món ăn, 1 loại hoa quả được chọn từ 5 loại nên có 5 cách chọn.
+ Ứng với mỗi cách chọn món ăn và 1 loại hoa quả thì một loại nước uống được chọn nên có 4 cách chọn.
Vậy theo quy tắc nhân ta có: 10.5.4 = 200 cách chọn
Bài 7: Trong một đội văn nghệ có 8 bạn nam và 6 bạn nữ. Hỏi có bao nhiêu cách chọn một đôi song ca nam
nữ ?
Hướng dẫn:
+ Chọn nam: có 8 cách chọn
+ Ứng với mỗi cách chọn nam, có 6 cách chọn nữa
Vậy tất cả có 6.8 = 48 cách chọn một đôi song ca.
Bài 8: Từ các chữ số 1; 5; 6; 7 có thể lập được bao nhiêu số tự nhiên :
a) Có 4 chữ số ?
b) Có 4 chữ số khác nhau ?

BÀI HỌC 2: HOÁN VỊ
1. Giai thừa là gì?
+ n giai thừa được ký hiệu n!
+ Cách tính: n! = n(n – 1)(n – 2).(n – 3) … 1
+ Quy ước 0! = 1! = 1
2. Định nghĩa
* Bài toán: Cho tập hợp A gồm n phần tử. Có bao nhiêu cách sắp xếp thứ tự n phần tử của A?
Ta có: Việc sắp xếp thứ tự n phần tử của A là một công việc gồm n – công đoạn:
+ Công đoạn 1: Chọn phần tử để sắp xếp vào vị trí thứ nhất : có n – cách
+ Công đoạn 2: Chọn phần tử để sắp xếp vào vị trí thứ hai : có n – 1 cách
+ Công đoạn 3: Chọn phần tử để sắp xếp vào vị trí thứ ba : có n – 2 cách
….
+ Công đoạn n: Chọn phần tử để sắp xếp vào vị trí thứ n : có 1 cách
Vậy ta có tất cả n(n – 1)(n – 2)(n – 3) … 1 = n! (cách)
* Định nghĩa:
Cho tập hợp A gồm n phần tử (n ³ 1) . Khi sắp xếp n phần tử THEO MỘT THỨ TỰ gọi là hoán vị các phần
tử của tập hợp A.
* Số các hoán vị: Pn = n!
VD1: Có 3 vận động viên An, Bình, Châu chạy thi. Nếu không kể trường hợp có 2 vận động viên cùng về
đích một lúc thì có bao nhiêu khả năng xảy ra ?
+ Do các vận động viên về đích được tính theo một thứ tự nên có 3 P = 3! = 3.2.1 = 6 khả năng
VD2: Trong một trận đá bóng, sau 2 hiệp phụ hai đội vẫn hòa nên phải thực hiện đá luân lưu 11m. Một đội
đã chọn được 5 cầu thủ để thực hiện 5 quả đá 11m. Hỏi có bao nhiêu cách sắp xếp đá phạt.
+ Do cách sắp xếp có tính theo thứ tự cầu thủ nên có 5 P = 5! = 5.4.3.2.1 = 120 cách sắp xếp
VD3: Từ các chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau ?
+ Có 5 P = 5! = 5.4.3.2.1 = 120 số
(Chú ý: Nếu từ các số 0; 1; 2; 3; 4 thì đáp số sẽ khác)
VD4: Một đoàn khách du lịch dự định đến tham quan 7 địa điểm A, B, C, D, E, F, G ở thủ đô Hà Nội. Hỏi có
bao nhiêu cách chọn ?
+ Vì các địa điểm tham quan có tính theo thứ tự nên có 7 P = 7! = 7.6.5.4.3.2.1 = 5040 cách chọn
VD5: Có bao nhiêu cách sắp xếp chỗ cho 3 người ngồi trong 1 bàn dài ?
+ Có 3 P = 3! = 3.2.1 = 6 cách sắp xếp.
3. Bài tập áp dụng hoán vị
Bài 1: Một giải bóng đá gồm 6 đội. Hỏi có bao nhiêu khả năng xảy ra về thứ tự giữa các đội ?
Hướng dẫn: Có 6 P = 6! = 6.5.4.3.2.1 = 720 khả năng.
Bài 2: Xét xem các số tự nhiên gồm 5 chữ số khác nhau lập nên từ các số 1; 2; 3; 4; 5. Hỏi trong các số đó có
bao nhiêu số:
a) Bắt đầu bởi chữ số 5 b) Không bắt đầu bằng chữ số 1
c) Bắt đầu bởi chữ số 2 và 3 d) Không bắt đầu bằng 345
Hướng dẫn:
a) Gọi số cần tìm là 1 2 3 4 5 1 a a a a a ;a = 5. Vì 4 chữ số 1; 2; 3; 4 vào các vị trí 2 3 4 5 a ;a ;a ;a nên là hoán vị
P4 = 4! = 24 số tự nhiên khác nhau và bắt đầu bằng chữ số 5.
b) Gọi số cần tìm là 1 2 3 4 5 a a a a a . Vì { } 1 a Î 2;3;4;5 nên có 4 cách chọn. Các số còn lại là hoán vị 4 P
Vậy có tất cả 4 4.P = 96 số thỏa mãn
c) Gọi số cần tìm là 3 4 5 23a a a . Vậy có 3 1.1.P = 6 số
d) Ta làm ngược lại: Số các số tự nhiên gồm 5 chữ số bắt đầu bằng 345 là 4 5 345a a . Vậy có 2 1.1.1.P = 2 số
Kết luận: Số các số tự nhiên thỏa mãn yêu cầu đề bài là 2 5!−1.1.1.P = 118 số
Bài 3: Từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 ta có thể lập được tất cả các số gồm 9 chữ số khác nhau :
a) Có bao nhiêu số được thành lập
b) Có bao nhiêu số chia hết cho 5
c) Có bao nhiêu số chẵn
Hướng dẫn:
a) Đáp số: 9! = 362.880 số
b) Ta thấy chữ số cuối cùng là 5 (để số cần tìm chia hết cho 5) nên có 1 cách chọn. 8 vị trí còn lại là hoán vị
vì vậy có 8! Cách chọn.
Kết luận: có 8!.1 = 40.320 số có 9 chữ số khác nhau chia hết cho 5
c) Ta thấy chữ số cuối cùng là 2; 4; 6; 8 (để số cần tìm là số chẵn) nên có 4 cách chọn. 8 vị trí còn lại là hoán
vị vì vậy có 8! Cách chọn.
Kết luận: có 8!.4 = 161.280 số có 9 chữ số khác nhau và là số chẵn.
Bài 4: Có 10 học sinh cùng ngồi trên một hàng ghế và chơi trò đổi chỗ. Cho rằng mỗi lần đổi chỗ hết 1 phút.
Hỏi thời gian họ đổi chỗ cho nhau là bao nhiêu ?
Hướng dẫn:
+ Số lần đổi chỗ là 10! = 3.628.800 lần
+ Thời gian họ đổi chỗ trong các tình huống là: 3.628.800 (khoảng 7 năm)
Bài 5: Một nhóm gồm 12 học sinh trong đó 5 nữ và 7 nam. Hỏi có bao nhiêu cách sắp xếp 12 học sinh thành
một hàng doc sao cho 5 học sinh nữ phải đứng liền nhau ?
Hướng dẫn: Dùng cách “buộc củi”
+ Coi 5 học sinh nữ đứng liền nhau như 1 nhóm X. Như vậy ta có 7 bạn nam và 1 nhóm X (coi như 8 bạn)
xếp thành một hàng dọc.
+ Xếp X và 7 học sinh nam có 8! Cách
+ Bây giờ mở nhóm X ra cho 5 bạn nữ hoán vị với nhau. Vậy xếp 5 bạn nữ trong nhóm X có 5! Cách.
Vậy theo quy tắc nhân ta có: 8! . 5! = 4.838.400 cách sắp xếp thỏa mãn yêu cầu bài toán.
Bài 6: Có 4 tem thư khác nhau và 4 bì thư khác nhau. Hỏi có bao nhiêu cách dán tem vào bì ?
Hướng dẫn:
(Cố định 4 bì thư (coi như 4 ghế ngồi), mỗi tem thư coi như 1 người di chuyển vào chỗ ngồi)
+ Cố định 4 bì thư. Mỗi hoán vị của 4 tem thư là 1 cách dán. Vậy có 4! = 24 cách dán tem vào bì
(Chú ý: không được vừa hoán vị tem vừa hoán vị bì thư, vì như vậy chắc chắn sẽ có lúc trùng nhau)
Bài 7: Cần sắp xếp 5 học sinh A, B, C, D, E thành một hàng ngang. Hỏi có bao nhiêu cách sắp xếp sao cho 2
học sinh A, và B luôn đứng ở đầu hàng ?
Hướng dẫn:
+ Coi 2 bạn A và B đứng cạnh nhau (đầu hàng) như một nhóm X. Như vậy ta có 3 bạn C, D, E và một nhóm
X (coi như 4 bạn)
+ X luôn đứng vị trí đầu nên có 1 cách xếp
+ 3 bạn còn lại có 3! Cách xếp.
+ 2 bạn trong nhóm X lại có 2! Cách xếp
Vậy ta có : 1.3!.2! = 12 cách sắp xếp
Bài 8: Từ 5 chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau, trong đó có
bao nhiêu số lẻ, bao nhiêu số không chia hết cho 5?
Hướng dẫn:
+ Ta có P5 = 5! = 120 số tự nhiên có 5 chữ số khác nhau
+ Gọi 1 2 3 4 5 a a a a a là số tự nhiên lẻ có 5 chữ sô khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
Khi đó { } 5 a Î 1;3;5 nên có 3 cách chọn, 4 số còn lại có 4! Cách chọn.
Vậy có 3.4! = 72 số tự nhiên lẻ có 5 chữ sô khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
+ Gọi 1 2 3 4 5 a a a a a là số tự nhiên chia hết cho 5 có 5 chữ sô khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
Khi đó 5 a = 5 nên có 1 cách chọn, 4 số còn lại có 4! Cách chọn.
Vậy có 1.4! = 24 số tự nhiên chia hết cho 5 có 5 chữ sô khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
Bài 9: Cần sắp xếp 3 học sinh nữ và 5 học sinh nam thành một hàng dọc:
a) Hỏi có bao nhiêu cách sắp xếp nếu 3 học sinh nữ luôn đứng liền nhau ?
b) Hỏi có bao nhiêu cách sắp xếp nêu học sinh đứng đầu là học sinh nữ và học sinh đứng cuối là học sinh
nam ?
Hướng dẫn:
a) Coi 3 bạn nữ cột lại thành một nhóm X, vậy có 1 nhóm X và 5 học sinh nam (coi như 6 học sinh) xếp
thành 1 hàng dọc. Xếp X và 5 bạn nam có 6! cách.
+ Sau khi xếp xong, mở nhóm X ra cho 5 học sinh nữ tự hoán vị cho nhau, vậy xếp 3 học sinh nữ trong
nhóm X sẽ có 3! Cách.
Kết luận: Vậy có 6!.3! = 4320 cách.
b)
+ Chọn 1 học sinh nữ đứng đầu hàng có 3 cách chọn
+ Chọn 1 học sinh nam đứng cuối hàng có 5 cách chọn.
+ Còn lại 6 vị trí ở giữa, ta chọn 6 học sinh còn lại xếp vào nên có 6! cách.
Kết luận: Tất cả có 3.5.6! = 10800 cách.
BÀI HỌC 3: CHỈNH HỢP
1. Bài toán:
Cho tập hợp A gồm n phần tử, lấy ra k phần tử của A (1 £ k £ n) và sắp xếp chúng theo một
THỨ TỰ. Hỏi có bao nhiêu cách sắp xếp ?
Hướng dẫn:
+ Công đoạn 1: Lấy phần tử thứ nhất có n cách
+ Công đoạn 2: Lấy phần tử thứ hai có n – 1 = (n – 2) + 1 cách
+ Công đoạn 3: Lấy phần tử thứ ba có n – 2 = (n – 3) + 1 cách
….
….
+ Công đoạn k: Lấy phần tử thứ k có n – (k – 1) = (n – k) + 1 cách
Vậy có tất cả: n(n −1)(n − 2) …(n − k +1) cách
2. Ví dụ:

BÀI HỌC 4: TỔ HỢP
1. Định nghĩa:
Cho tập hợp A gồm n phân tử và số nguyên k với 1£ k £ n . Mỗi tập hợp con của A có k phần tử được gọi là 1 tổ hợp chập k của n phần tử, gọi tắt là một tổ hợp chập k của A (không tính theo thứ tự)

2. Tính chất:
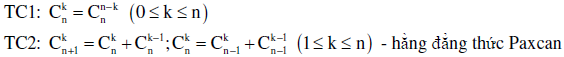
Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập và ví dụ liên quan đến hoán vị chỉnh hợp tổ hợp. Để học tốt dạng bài tập này trong chuyên đề này, các em cần phải thực sự hiểu bản chất. Sau đó tích cực làm bài tập để tìm ra được các lỗi nhầm lẫn giữa hoán vị, chỉnh hợp và tổ hợp. Làm bài tập càng nhiều thì khả năng phản xạ cho từng dạng bài sẽ càng tăng. Cuối cùng thì xin chúc các em học tốt!
Xem thêm video
Từ khóa:
- hoán vị chỉnh hợp tổ hợp 11
- nâng cao quy tắc đếm hoán vị chỉnh hợp tổ hợp
- hoán vị chỉnh hợp tổ hợp
- lý thuyết hoán vị chỉnh hợp tổ hợp nâng cao
- hoán vị chỉnh hợp tổ hợp lớp 11 đặng việt hùng
- bảng so sánh hoán vị chỉnh hợp tổ hợp
- bài 2 hoán vị chỉnh hợp tổ hợp violet
- các bài toán tổ hợp hay và khó




 056.3753648
056.3753648
 Chat FB
Chat FB