Cực trị số phức, bất đẳng thức số phức và bài tập trắc nghiệm

Để giải bài tập về cực trị số phức, ta sử dụng một số bất đẳng thức số phức. Như là bất đẳng thức tam giác, công thức trung tuyền, tập hợp điểm. Ở tài liệu này, chúng tôi giới thiệu đến các em một số dạng toán về số phức cũng như cực trị số phức. Các bài toán đều được phân dạng rõ ràng và chi tiết.

TẢI XUỐNG PDF ↓

Bài tập cực trị số phức

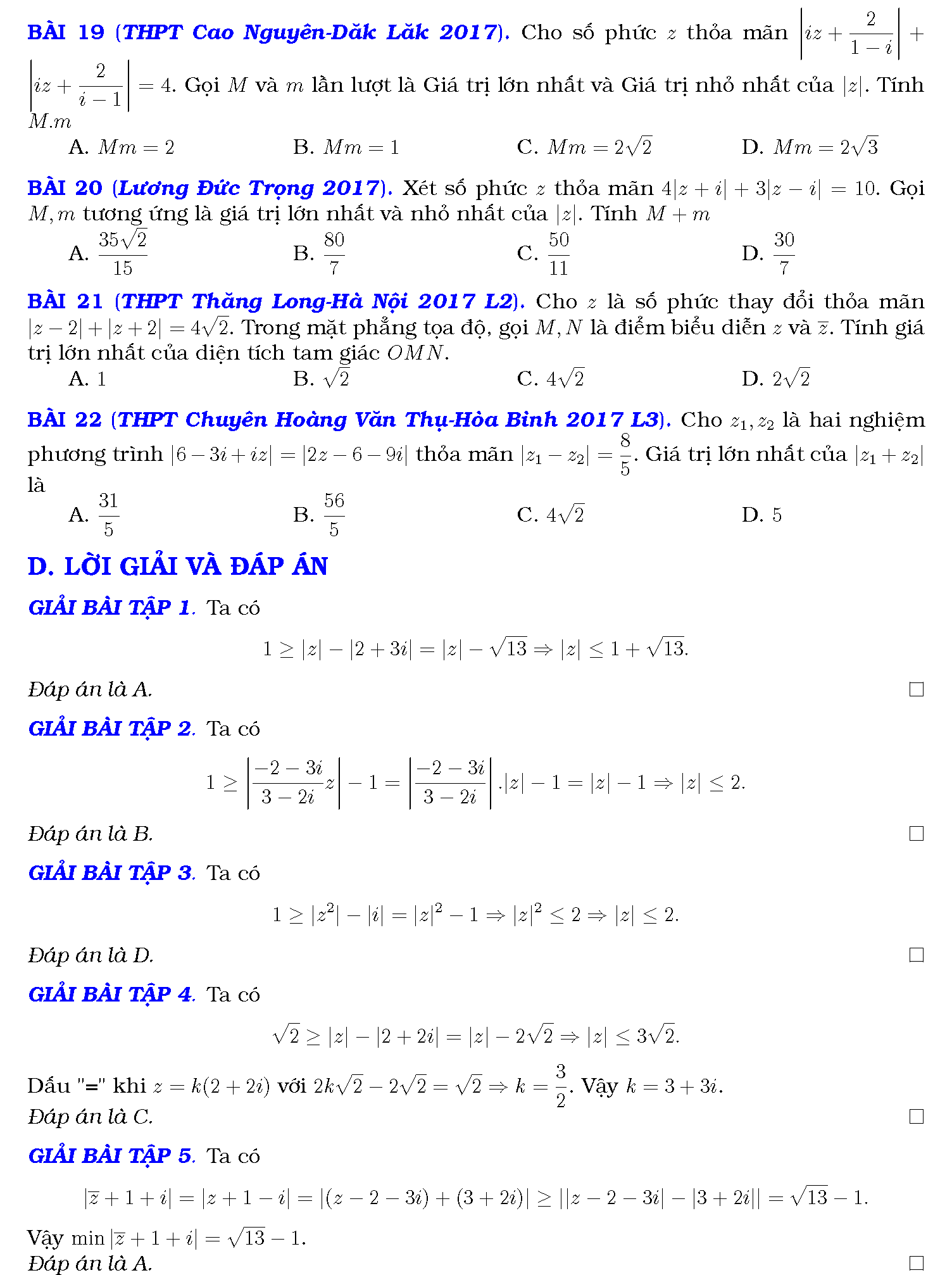
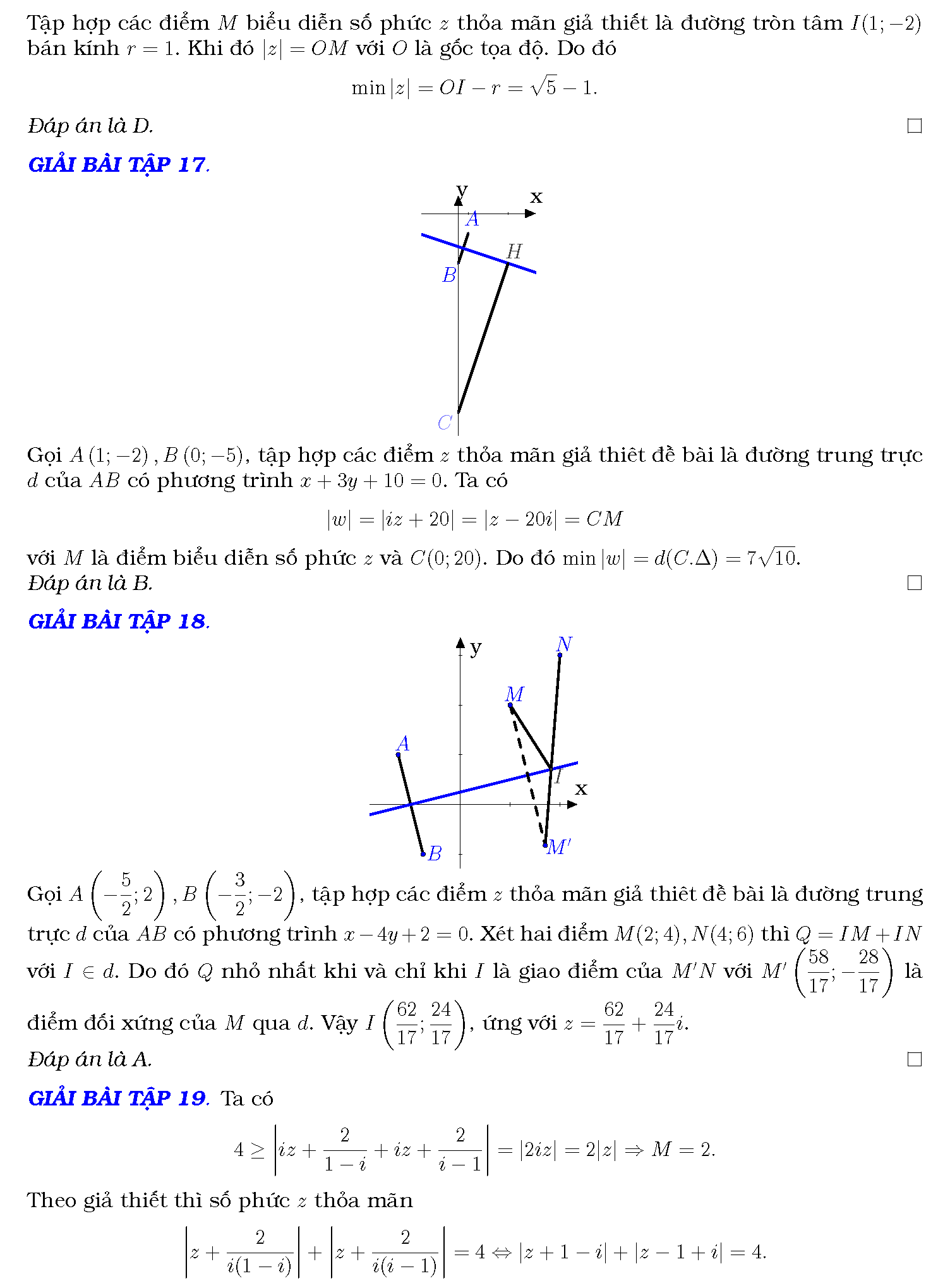
Phương pháp giải toán cực trị số phức

Có nhiều cách để giải một bài toán. Riêng dạng toán cực trị số phức cũng không ngoại lệ. Người ta thường đi theo hai hướng sau đây:

• Phương pháp đại số
• Phương pháp hình học

Các phương pháp đều bổ trợ cho nhau. Việc sử dụng  phương pháp nào còn tùy thuộc vào sự lựa chọn cũng như kiến thức từng người đối với dạng toán.

Kiến thức cần nắm về số phức

Bất đẳng thức tam giác:

+ |z1 + z2| ≤ |z1| + |z2|, dấu “=” khi z1 = kz2 với k ≥ 0
+ |z1 − z2| ≤ |z1| + |z2|, dấu “=” khi z1 = kz2 với k ≤ 0
+ |z1 + z2| ≥ ||z1| − |z2||, dấu “=” khi z1 = kz2 với k ≤ 0
+ |z1 − z2| ≥ ||z1| − |z2||, dấu “=” khi z1 = kz2 với k ≥ 0

Công thức trung tuyến:

|z1 + z2|^2 + |z1 − z2|^2 = 2(|z1|^2 + |z2|^2)

Tập hợp điểm

+ |z − (a + bi)| = r: Đường tròn tâm I(a; b) bán kính r
+ |z − (a1 + b1i)| = |z − (a2 + b2i)|: Đường trung trực của AB với A(a1; b1), B(a2; b2)
+ |z − (a1 + b1i)| + |z − (a2 + b2i)| = 2a:
– Đoạn thẳng AB với A(a1; b1), B(a2; b2) nếu 2a = AB
– Elip (E) nhận A, B làm hai tiêu điểm với độ dài trục lớn là 2a nếu 2a > AB
Đặc biệt |z + c| + |z − c| = 2a: Elip (E) : x^2/a^2 + y^2/b^2 = 1 với b = √(a^2 − c^2)

Xem thêm: Bất đẳng thức bernoulli 

Câu hỏi phổ biến về cực trị trong số phức

• Cho số phức Z, hỏi mô đun lớn nhất của số phức Z là gì?
• Trong các số phức Z thỏa mãn yêu cầu đề bài. Tìm số phức Z có mô đun nhỏ nhất
• Cho số phức Z thỏa mãn. Giá trị nhỏ nhất của |Z| là?
• Cho số phức Z thỏa mãn điều kiện cho trước. Biểu thức |Z| có giá trị lớn nhất là?
• Cho số phức z thỏa mãn điều kiện cho trước. Biểu thức Q = m.z + n.|z| đạt giá trị nhỏ nhất tại z = ai + b. Tính giá trị của biểu thức P = a – 4b

Vậy là chúng ta vừa tìm hiểu xong một số định nghĩa về cực trị số phức, bất đẳng thức số phức cũng như một vài bài tập đặc trưng. Các dạng toán số phức ngày càng được khai thác nhiều trong toán trắc nghiệm. Do đó, các em học sinh cần phải lưu ý phần số phức nếu muốn đạt điểm cao. Các bài tập số phức thường mang tính kế thừa là chủ yếu. Do đó, các dạng toán lặp đi lặp lại nhiều. Muốn học tốt chỉ cần nắm vững một dạng nhất định.

Các câu hỏi thường gặp về cực trị số phức, bất đẳng thức số phức

Xem thêm: Bất đẳng thức trị tuyệt đối

Xem thêm video

video trên Thầy Linh dạy toán

video trên Trung tâm giáo dục Tam Nguyên