Tóm tắt tài liệu
Bài tập phương trình đường tròn lớp 10 bao gồm một số dạng cơ bản như: Nhận dạng một phương trình bậc hai là phương trình đường tròn; Tìm tâm vồ bán kính đường tròn; Lập phương trình của đường tròn; Lập phương trình tiếp tuyến, của đường tròn. Trong bài viết này sẽ trình bày tất cả các dạng toán trên, cũng như phương pháp giải và bài tập ứng dụng có đáp án. Phục vụ nhu cầu học sinh, chúng tôi đã tổng hợp vào một số file pdf dưới đây. Bạn đọc có nhu cầu có thể tải về và in ra để làm bài tập.
Lý thuyết cơ bản
Phương trình đường tròn
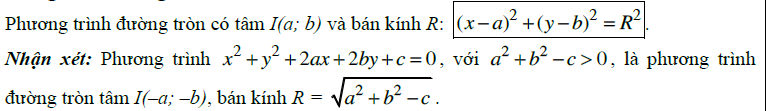
Phương trình tiếp tuyến của đường tròn

Phân dạng bài tập
Dạng 1: Xác định tâm và bán kính đường tròn
– Nếu phương trình đường tròn \[(C)\] có dạng: \[{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}\] thì (C) có tâm I(a; b) và bán kính R.
– Nếu phương trình đường tròn (C) có dạng: \[{{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\] thì – Biến đổi đưa về dạng \[{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}\] – Tâm \[I(-a;-b)\], bán kính \[R=\sqrt{{{a}^{2}}+{{b}^{2}}-c}\]
– Chú ý: Phương trình \[{{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\] là phương trình đường tròn nếu thoả mãn điều kiện: \[{{a}^{2}}+{{b}^{2}}-c>0\]

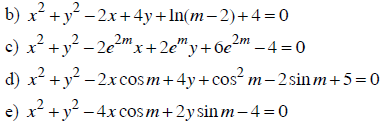
Dạng 2: Lập phương trình đường tròn
Loại 1: (C) có tâm I và đi qua điểm A
- bán kính R = IA
Loại 2: (C) tâm I và tiếp xúc với đường thẳng \[\Delta \]
- Bán kính \[R=d(I,\Delta )\]
Loại 3: (C) có đường kính AB.
- Tâm I là trung điểm AB
- Bán kính \[R=\frac{AB}{2}\]
Loại 4: (C) đi qua hai điểm A, B và có tâm I nằm trên đường thẳng \[\Delta \]
- Viết phương trình đường trung trực d của đoạn AB.
- Xác định tâm I là giao điểm của d và \[\Delta \]
- Bán kính R = IA
Loại 5: (C) đi qua 2 điểm A và B và tiếp xúc với đường thẳng \[\Delta \]
- Viết phương trình đường trung trực d của đoạn thẳng AB
- Tâm I của (C) thỏa mãn: \[\left\{ \begin{matrix}I\in D \\d(I,\Delta )=IA \\\end{matrix} \right.\]
- Bán kính R = IA

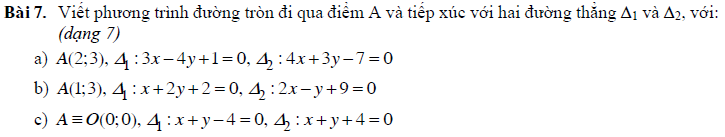

Dạng 3: Tìm tập hợp điểm
1. Tập hợp các tâm đường tròn
Để tìm tập hợp các tâm I của đường tròn (C), ta có thể thực hiện như sau:
- a) Tìm giá trị của m để tồn tại tâm I.
- b) Tìm toạ độ tâm I. Giả sử: \[I\left\{ \begin{matrix}x=f(m) \\y=g(m) \\\end{matrix} \right.\].
- c) Khử m giữa x và y ta được phương trình F(x; y) = 0.
- d) Giới hạn: Dựa vào điều kiện của m ở a) để giới hạn miền của x hoặc y.
- e) Kết luận: Phương trình tập hợp điểm là F(x; y) = 0 cùng với phần giới hạn ở d).
2. Tập hợp điểm là đường tròn: Thực hiện tương tự như trên.


Dạng 4: Vị trí tương đối của đường thẳng d và đường tròn (C)
Để biện luận số giao điểm của đường thẳng \[d:Ax+By+C=0\] và đường tròn \[(C):{{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\], ta có thể thực hiện như sau:.
Cách 1: So sánh khoảng cách từ tâm I đến d với bán kính R.
– Xác định tâm I và bán kính R của (C).
– Tính khoảng cách từ I đến d.
+ \[d(I,d)<R\Leftrightarrow \] cắt (C) tại hai điểm phân biệt.
+ \[d(I,d)=R\Leftrightarrow \] tiếp xúc với (C).
+ \[d(I,d)>R\Leftrightarrow \] và (C) không có điểm chung.
Cách 2: Toạ độ giao điểm (nếu có) của d và (C) là nghiệm của hệ phương trình:\[\left\{ \begin{matrix}Ax+By+C=0 \\{{x}^{2}}+{{y}^{2}}+2ax+2by+c=0 \\\end{matrix} \right.\](*)
- Hệ (*) có 2 nghiệm \[\Leftrightarrow \] d cắt (C) tại hai điểm phân biệt.
- Hệ (*) có 1 nghiệm \[\Leftrightarrow \] d tiếp xúc với (C).
- Hệ (*) vô nghiệm \[\Leftrightarrow \] d và (C) không có điểm chung.
![]()

Dạng 5: Vị trí tương đối của hai đường tròn (C1) và (C2)

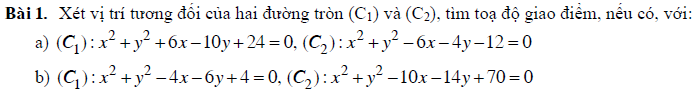

Dạng 6: Tiếp tuyến của đường tròn (C)



Bài tập phương trình đường tròn lớp 10


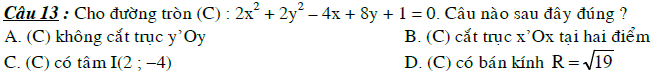

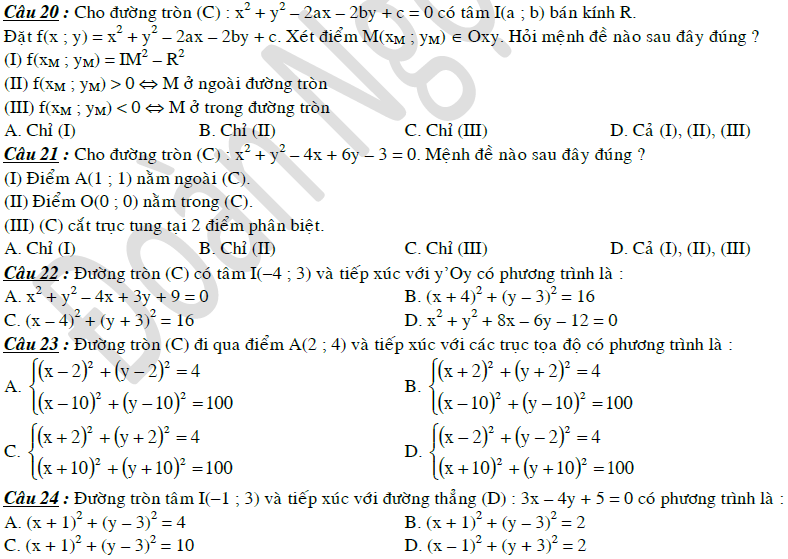
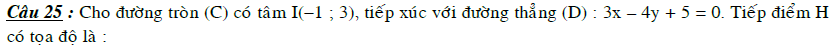



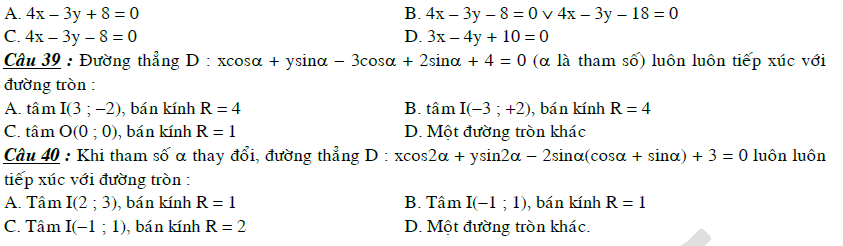
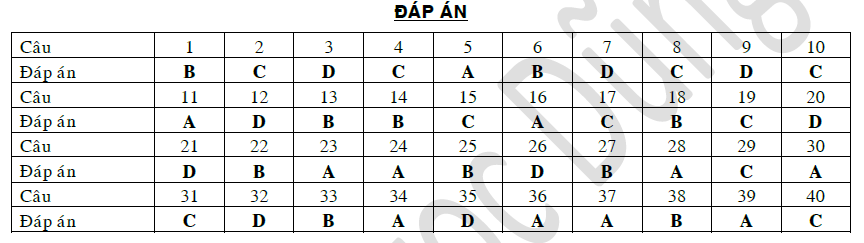
Bài tập tự luận có lời giải về đường tròn


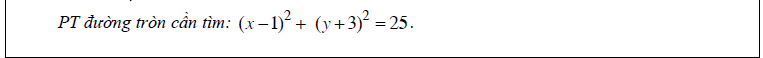
Vậy là chúng ta vừa tìm hiểu xong khá là nhiều bài tập phương trình đường tròn lớp 10. Để đạt được kết quả cao nhất trong chuyên đề này. Các em cần phải rèn luyện một cách thật kĩ lưỡng. Các file bài tập đều ở dưới dạng pdf, do đó, nếu các em có nhu cầu có thể in ra và làm bài một cách dễ dàng. Bài viết phương trình đường tròn là một trong những bài rất tâm huyết của tailieure…do đó các tài liệu được tuyển chọn rất kĩ. Lời cuối, xin chúc các em học sinh học tập thật tốt, đạt kết quả cao.
Xem thêm video
Từ khóa:
- lý thuyết phương trình đường tròn lớp 10
- giải bài tập phương trình đường tròn lớp 10 sgk
- cách nhận biết phương trình đường tròn
- bài tập về đường tròn lớp 9
- phuong trinh duong tron nang cao
- viết phương trình đường tròn có tâm thuộc đường thẳng
- phương trình đường tròn tiếp xúc với đường thẳng
- giải bài tập toán hình 10 trang 83



 056.3753648
056.3753648
 Chat FB
Chat FB