Bài tập hàm số lượng giác lớp 11

Bài tập hàm số lượng giác gồm khá nhiều dạng biến thể cũng như với lượng kiến thức khá phong phú. Do đó, một tài liệu liệu tổng hợp tất cả bài tập chương hàm số lượng giác là một điều cần thiết. Đó là lý do chúng tôi quyết định đăng tải tài liệu này. Tài liệu gồm 237 trang do giáo viên Đặng Việt Đông biên soạn bao trùm tất cả các vấn đề lượng giác – chương trình lớp 11,12. Đây là một tài liệu vô cùng cần thiết khi nó đi đúng theo xu hướng trắc nghiệm của bộ GD đề ra, nhắm đúng vào trọng tâm chương lượng giác.

TẢI XUỐNG PDF ↓

PHẦN 1. HÀM SỐ LƯỢNG GIÁC

Trước khi tìm hiểu các dạng toán và bài tập liên quan đến hàm số lượng giác, chúng ta cùng điểm qua một vài vấn đề lý thuyết cực kì quan trọng trong phần này. Phần lý thuyết nhắc lại 4 hàm số lượng giác mà chúng ta vẫn thường hay gặp: \[\sin \alpha ,cos\alpha ,\tan \alpha ,\cot \alpha \]

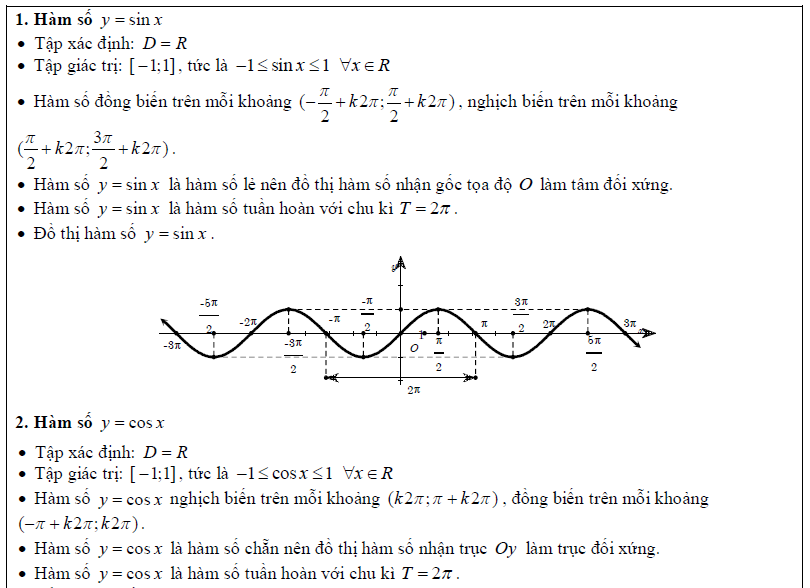
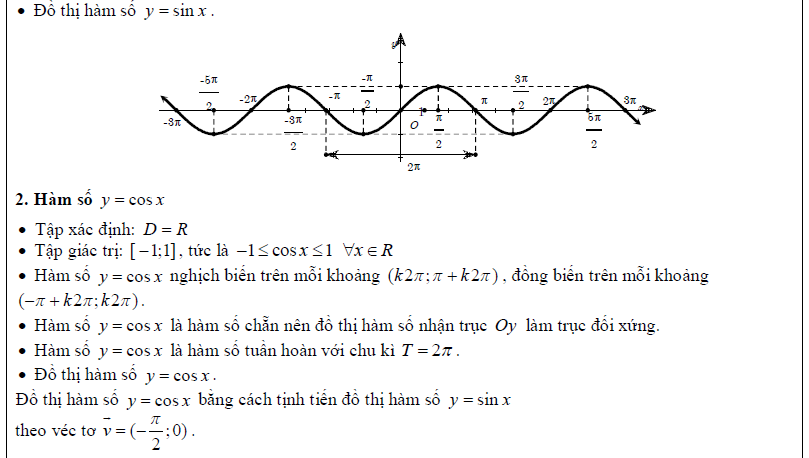
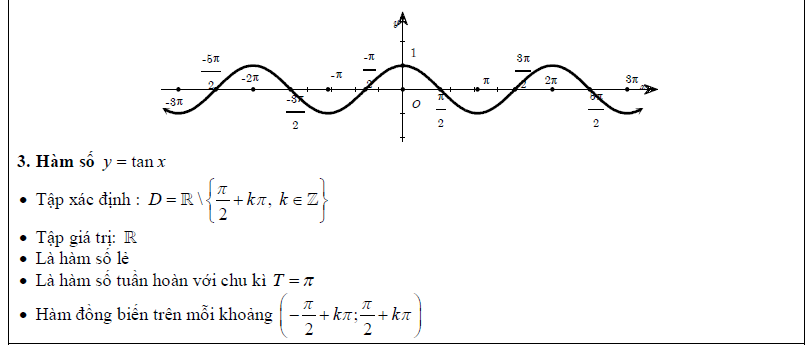
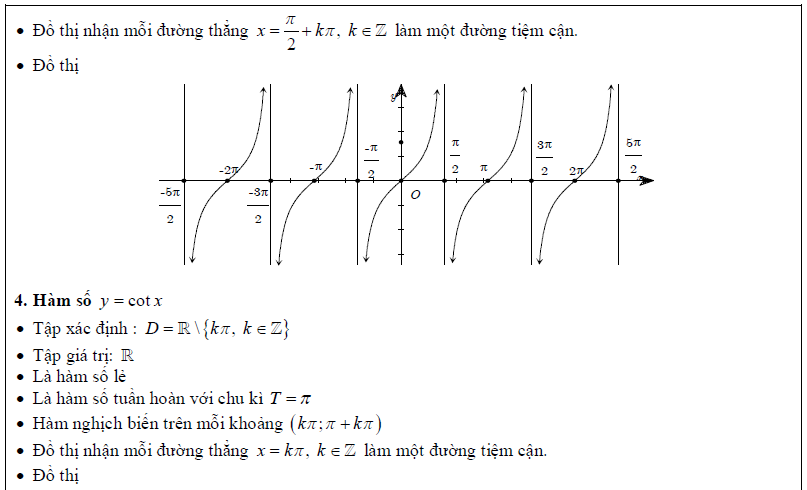
Dạng 1. Tìm tập xác định, tập giá trị, xét tính chẵn lẻ, chu kỳ của hàm số

• Hàm số \[y=\sqrt{f(x)}\] tồn tại \[\Leftrightarrow f(x)\ge 0\] và \[f(x)\] tồn tại
• Hàm số \[y=\frac{1}{f(x)}\] tồn tại \[f(x)\ne 0\] và \[f(x)\] tồn tại
• \[\sin u(x)\ne 0\Leftrightarrow u(x)=k\pi ,k\in Z\]
• \[\cos u(x)\ne 0\Leftrightarrow u(x)=\frac{\pi }{2}+k\pi ,k\in Z\]

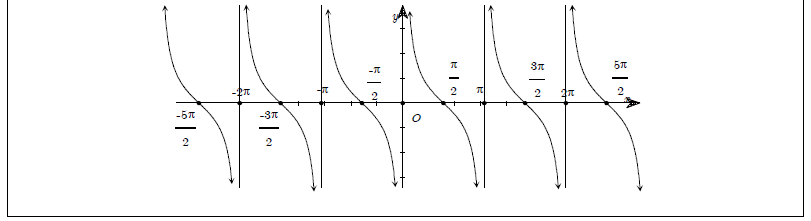
Dạng 2. Sự biến thiên và đồ thị hàm số lượng giác

Cho hàm số \[y=f(x)\] tuần hoàn với chu kì T

• Để khảo sát sự biến thiên và vẽ đồ thị của hàm số, ta chỉ cần khảo sát và vẽ đồ thị hàm số trên một đoạn có độ dài bằng T sau đó ta tịnh tiến theo các véc tơ \[k.\overrightarrow{v,}\] ta được toàn bộ đồ thị của hàm số \[f(x)=k\]
• Số nghiệm của phương trình \[y=f(x)\] (với k là hằng số) chính bằng số giao điểm của hai đồ thị \[y=k\] và \[f(x)\ge 0\].
• Nghiệm của bất phương trình \[f(x)\ge 0\] là miền x mà đồ thị hàm số \[y=f(x)\] nằm trên trục\[Ox\].

Dạng 3. Giá trị lớn nhất và nhỏ nhất của hàm số lượng giác

PHẦN 2. PHƯƠNG TRÌNH LƯỢNG GIÁC

Ta cùng tìm hiểu một số loại phương trình lượng giác để có thể biết cách giải khi gặp từng dạng bởi lẽ mỗi dạng sẽ có những cách giải hoàn toàn khác nhau. Xem thêm trong tài liệu để biết được chi tiết tài liệu có những phần mục gì

• Phương trình lượng giác cơ bản và phương trình bậc nhất với một hàm số lượng giác
• Phương trình quy về bậc nhất với một hàm số lượng giác
• Phương trình bậc hai và quy về bậc hai với một hàm số lượng giác
• Phương trình đẳng cấp với sin và cosin
• Phương trình đối xứng và dạng đối xứng với sin và cosin

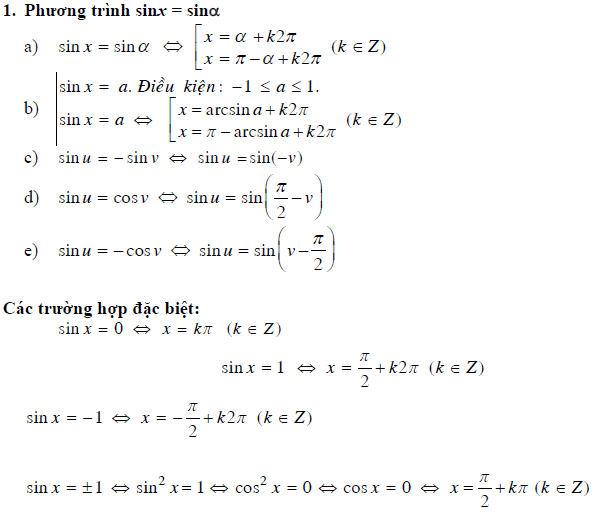
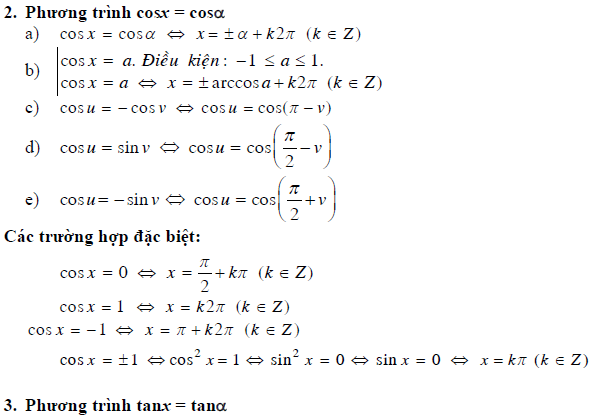
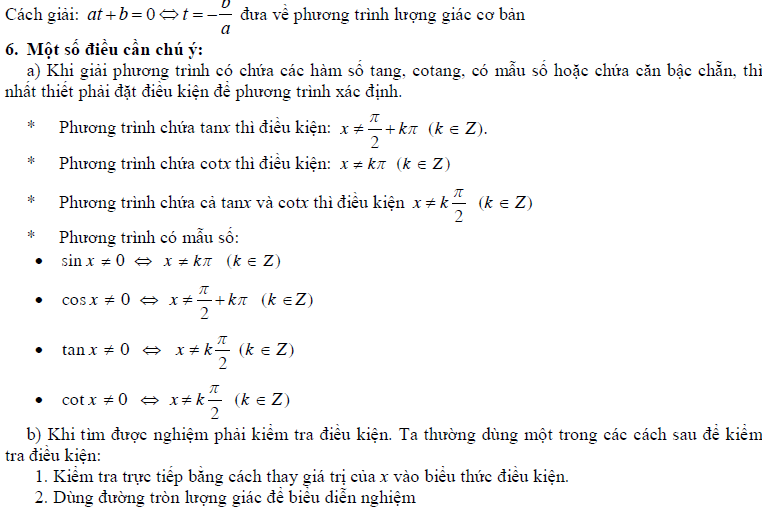
PHẦN 3. BÀI TẬP TỔNG HỢP

Một số bài tập tổng hợp về hàm số lượng giác và phương trình lượng giác được giới thiệu dưới đây. Các em có thể thực hiện từng dạng bài để nắm được cách làm chi tiết cho mỗi dạng:

• Phương trình bậc nhất với sin và cosin
• Phương trình quy về bậc nhất với sin và cosin
• Phương trình lượng giác đưa về tích
• Phương trình lượng giác không thường gặp

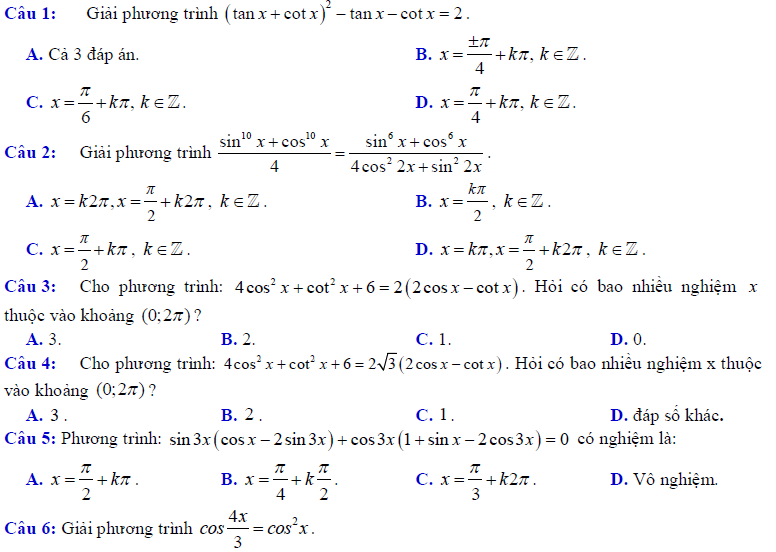
Vậy qua hơn 200 trang, có lẽ chúng ta đã tìm hiểu được tất cả các dạng bài tập hàm số lượng giác và phương trình lượng giác. Các dạng toán không quá khó, tuy nhiên để nắm vững các em cần phải hiểu rõ bản chất bài toán cũng như thuộc lòng các công thức toán học. Để thuận tiện hơn cho việc học, các em có thể tải tài liệu về và thực hành mỗi ngày. Chúc các em thành công.

Xem thêm video

video trên Thầy Linh dạy toán

video trên Trung tâm giáo dục Tam Nguyên

Từ khóa bài viết: