Tóm tắt tài liệu
Có khá nhiều phương pháp tìm cực trị của hàm số, tuy nhiên hôm nay tailieure chỉ giới thiệu đến các em 2 cách phổ biến nhất, áp dụng thường xuyên nhất vào các bài tập. Cả 2 cách trên đều đảm bảo cho bạn đọc tìm cực trị một cách đầy đủ, chi tiết về cách trình bày để đạt điểm tối đa nhất. Các đọc giả có thể rút kinh nghiệm thông qua các ví dụ sau đây.
Phương pháp :Để tìm cực trị của một hàm số y = f(x) ta có các cách sau
Quy tắc 1 : Áp dụng định lý 2
+) Tìm \[f'(x)\]
+) Tìm các điểm \[{{x}_{i}}\](\[i=1,2,3…\]) tại đó đạo hàm bằng \[0\] hoặc hàm số liên tục nhưng không có đạo hàm.
+) Xét dấu của \[f'(x)\]. Nếu \[f'(x)\] đổi dấu khi x đi qua xo thì hàm số có cực trị tại xo.
Quy tắc 2 : Áp dụng định lý 3
+) Tìm \[f'(x)\]
+) Tìm các nghiệm \[{{x}_{i}}\] (\[i=1,2,3…\]) của phương trình \[f'(x)=0\].
+) Với mỗi \[{{x}_{i}}\] ta tính \[f”(x)\]:
Nếu \[f”({{x}_{i}})>0\] thì hàm số đạt cực tiểu tại \[{{x}_{i}}\]
Nếu \[f”({{x}_{i}})<0\] thì hàm số đạt cực đại tại \[{{x}_{i}}\]
Bài tập ứng dụng tìm cực trị của hàm số
Để giúp các em làm quen với dạng bài tập tìm các điểm cực trị của một hàm số bất kì, tailieure xin giới thiệu đến các em một số ví dụ mẫu như sau:
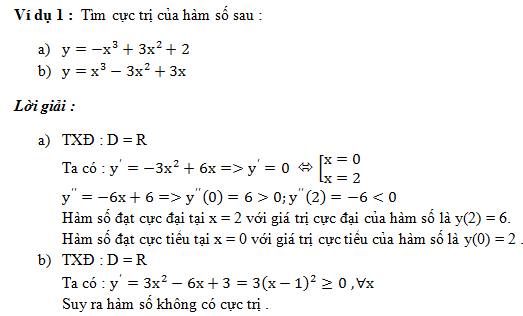
Chú ý: Đối với hàm bậc bốn vì đạo hàm là đa thức bậc ba nên hàm chỉ có thể có một cực trị hoặc ba cực trị. Hàm số có một cực trị khi phương trình có một hoặc hai nghiệm (1 nghiệm đơn, 1 nghiệm kép), hàm số có ba cực trị khi phương trình có ba nghiệm phân biệt .
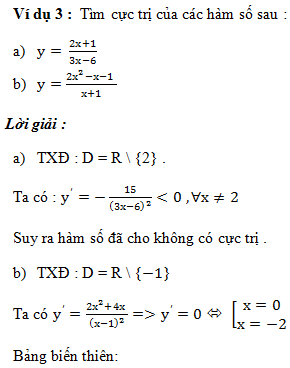
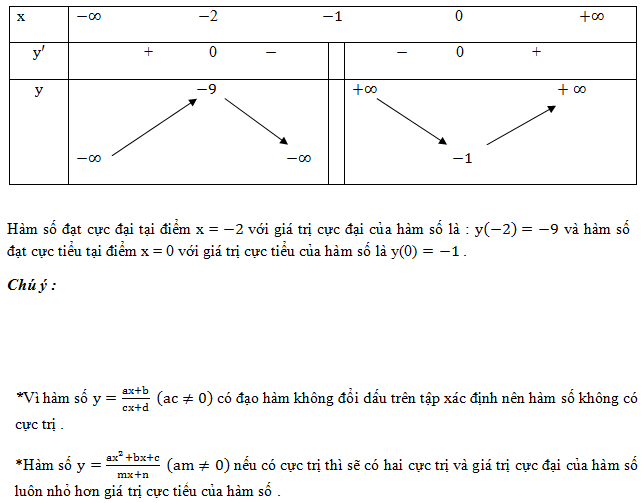
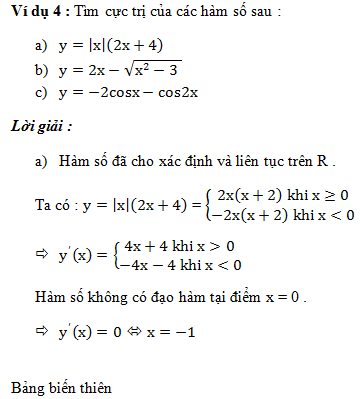
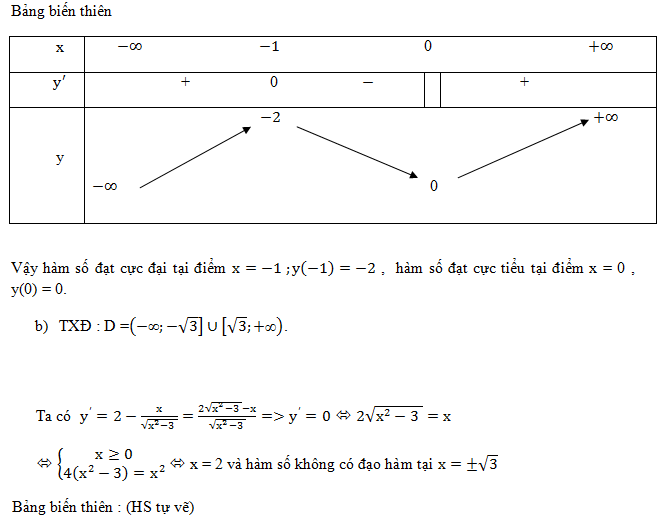
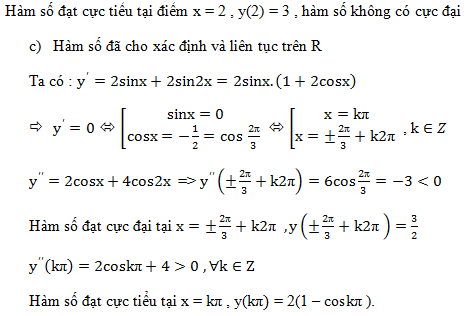
Để tải các ví dụ mẫu phía trên các em có thể tải tại file pdf này:
CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆUĐể xem thêm nhiều bài tập tìm cực trị của hàm số, các em có thể truy cập tại các bài viết liên quan dưới đây:
