Trắc nghiệm giới hạn hàm số, dãy số hay nhất

Để tiếp nối các bài viết trong chuyên đề giới hạn hàm số, ở bài viết này chúng tôi muốn giới thiệu đến em bộ tài liệu trắc nghiệm 58 trang về giới hạn hàm số, dãy số. Tài liệu gồm hơn 100 câu trắc nghiệm giới hạn hàm số, ngoài ra còn bổ sung thêm chuyên đề dãy số giúp các em dễ dàng hệ thống lại kiến thức liên quan khi làm bài tập. Các câu trắc nghiệm giới hạn đi từ dễ đến khó và có lời giải chi tiết.

Mục lục tài liệu giới hạn hàm số

I. Giới hạn hữu hạn của một hàm số tại một điểm

1. Định nghĩa về giới hạn hàm số

2. Các định lí về giới hạn hữu hạn

3. Giới hạn một bên

II. Giới hạn hữu hạn của hàm số tại vô cực

III. Giới hạn vô cực của hàm số

1. Giới hạn vô cực

2. Một vài giới hạn đặc biệt

3. Một vài qui tắc tính giới hạn vô cực

IV. Các câu hỏi trắc nghiệm về giới hạn hàm số

1. Giới hạn hữu hạn

2. Giới hạn một bên

3. Giới hạn tại vô cực

4. Dạng vô định \[\frac{0}{0}\]

5. Dạng vô định \[\frac{\infty }{\infty }\]

6. Dạng vô định \[\infty -\infty \]

7. Dạng vô định \[0.\infty \]

8. Câu hỏi trắc nghiệm về tính liên tục của hàm số

Mục lục tài liệu giới hạn dãy số

I. Giới hạn hữu hạn của dãy số

II. Định lí về giới hạn hữu hạn của dãy số

III. Tổng của cấp số nhân lùi vô hạn

IV. Giới hạn vô cực

V. Trắc nghiệm giới hạn dãy số

1. Dãy số dạng phân thức

2. Dãy số chứa căn thức

3. Dãy số chứa hàm số lũy thừa, mũ, logarit

4. Trắc nghiệm tổng của cấp số nhân lùi vô hạn

Trích đoạn câu hỏi trắc nghiệm giới hạn trong tài liệu

1. Giá trị của giới hạn \[\underset{x\to 2}{\mathop{\lim }}\,(3{{x}^{2}}+7x+11)\] là:

Lời giải: \[\underset{x\to 2}{\mathop{\lim }}\,(3{{x}^{2}}+7x+11)={{3.2}^{2}}+7.3+11=37\to \] chọn A

2. Giá trị của giới hạn \[\underset{x\to \sqrt{3}}{\mathop{\lim }}\,\left| {{x}^{2}}-4 \right|\] là:

Lời giải: \[\underset{x\to \sqrt{3}}{\mathop{\lim }}\,\left| {{x}^{2}}-4 \right|=\left| {{(\sqrt{3})}^{2}}-4 \right|=1\to \] chọn B

3. Giá trị của giới hạn \[\underset{x\to 0}{\mathop{\lim }}\,{{x}^{2}}.\sin \frac{1}{2}\] là:

Lời giải: \[\underset{x\to 0}{\mathop{\lim }}\,{{x}^{2}}.\sin \frac{1}{2}=0.\sin \frac{1}{2}=0\to \] chọn B

4. Cho hàm số \[f(x)=\left\{ \begin{matrix}\frac{{{x}^{2}}+1}{1-x},x<1 \\\sqrt{2x-2},x\ge 1 \\\end{matrix} \right.\]. Khi đó \[\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)\] là:

Lời giải: \[\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{{{x}^{2}}+1}{1-x}=+\infty \] vì \[\left\{ \begin{matrix}\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,({{x}^{2}}+1)=2 \\\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,(1-x)=0 \\\end{matrix} \right.\] chọn A

5. Định lí 1 về giới hạn hữu hạn của hàm số

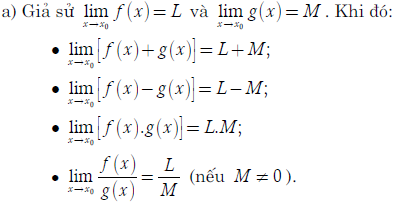
Xem thêm video

video trên Thầy Linh dạy toán

video trên Trung tâm giáo dục Tam Nguyên

Từ khóa bài viết: giới hạn hàm số, trắc nghiệm, dãy số, công thức.

Chuyên mục: Giới hạn hàm số

Nguồn bài viết: https://toanmath.com/