Tóm tắt tài liệu
Một trong những kì thi quan trọng đối với các bạn học sinh có lẽ là kì thi học sinh giỏi. Kì thì này sẽ bồi dưỡng tư duy, giúp cho các bạn học sinh sáng tạo hơn. Và với việc tuyển chọn học sinh giỏi cấp Huyện, Tỉnh đối với bộ môn Toán 11. Chúng tôi xin gửi đến các bạn học sinh bộ đề thi học sinh giỏi toán 11 nhằm giúp các bạn ôn luyện một cách dễ dàng.
Danh sách đề thi học sinh giỏi toán 11
– SỞ GD&ĐT QUẢNG BÌNH
– SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ TĨNH
– SỞ GD&ĐT NGHỆ AN
– SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
Cấu trúc đề thi
Mỗi đề thi sẽ bao gồm từ 4 đến 6 câu hỏi tự luận.
Một số câu hỏi trong đề thi
Câu 1: Một hộp chứa 17 quả cầu đánh số từ 1 đến 17. Lấy ngẫu nhiên đồng thời 3 quả cầu. Tính xác suất sao cho tổng các số ghi trên 3 quả cầu đó là một số chẵn.
Câu 2: Cho tam giác ABC cân tại A. Gọi D là trung điểm cạnh AC và M là trung điểm cạnh BC. Đoạn thẳng AM cắt đường tròn ngoại tiếp tam giác BCD tại điểm E. Đường thẳng BD cắt đường tròn ngoại tiếp tam giác ABE tại điểm F khác B. Đường thẳng AF cắt đường thẳng BE tại I, đường thẳng CI cắt đường thẳng BD tại K.
a. Chứng minh rằng DA= DF.
b. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác ABK.
Câu 3: Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC, G là trọng tâm tam giác ABM ; điểm D(7; -2) nằm trên đoạn MC sao cho GA = GD. Viết phương trình đường thẳng AB, biết hoành độ của A nhỏ hơn 4 và AG có phương trình 3x- y- 13= 0.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD // BC), BC = 2a, AB= AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD. Biết SD vuông góc với AC.
a) Chứng minh mặt phẳng (SBC) vuông góc mặt phẳng (ABCD). Tính độ dài đoạn thẳng SD.
b) Mặt phẳng ( a) đi qua điểm M thuộc đoạn thẳng OD ( M khác O và D) và song song với đường thẳng SD và AC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( a) biết MD = x. Tìm x để diện tích thiết diện lớn nhất.
Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD. Hình chiếu vuông góc của điểm D lên các đường thẳng AB, BC lần lượt là M( 2;- 2), N (- 2; 2) đường thẳng BD có phương trình 3x- 5y+ 1= 0. Tìm tọa độ điểm A.
Câu 6: Năm 2018 là năm kỷ niệm 50 năm Chiến thắng Đồng Lộc (24/7/1968-24/7/2018), trường học X cho học sinh trong các đội tuyển học sinh giỏi Toán khối 10, khối 11 của trường về tham quan khu di tích Ngã ba Đồng lộc. Biết rằng đội tuyển Toán khối 10 có 4 em gồm 2 nam, 2 nữ; đội tuyển Toán khối 11 có 4 em gồm 3 nam, 1 nữ. Trong đợt tham quan thứ nhất, trường chọn 3 học sinh với yêu cầu có cả đội tuyển 10, cả đội tuyển 11; có cả nam và cả nữ. Hỏi có bao nhiêu cách chọn.
Câu 7: Một đoàn tàu có 4 toa đỗ ở sân ga.có 4 hành khách bước lên tàu. Hỏi
a. Có bao nhiêu trường hợp có thể xảy ra về cách chọn toa của 4 hành khách
b. Có bao nhiêu trường hợp mà mỗi toa có 1 người lên
c. Có bao nhiêu trường hợp mà 1 toa có 3 người lên,1 toa có 1 ngưới lên và hai toa còn lại không có ai lên
Câu 8: Cho hình chóp SABCD, có đáy là hình thoi cạnh a, SA= SB= SC= a. Đặt SD= x (0< x< a.căn( 3) )
.a) Tính góc giữa đường thẳng SB và mặt phẳng (ABCD), biết rằng x= a.
b) Tìm x theo a để tích AC SD. đạt giá trị lớn nhất.
Câu 9: Một tứ giác có bốn góc tạo thành một cấp số nhân và số đo góc lớn nhất gấp 8 lần số đo góc nhỏ nhất. Tính số đo các góc của tứ giác trên.
Đáp số đề thi học sinh giỏi toán 11
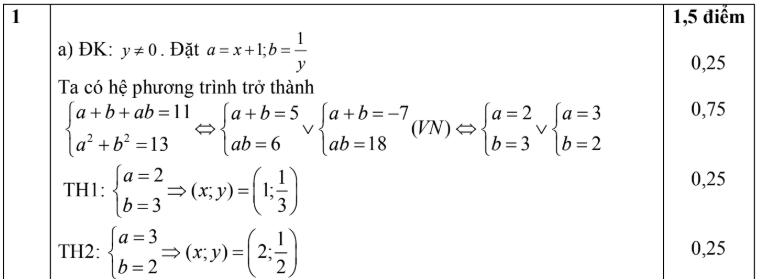
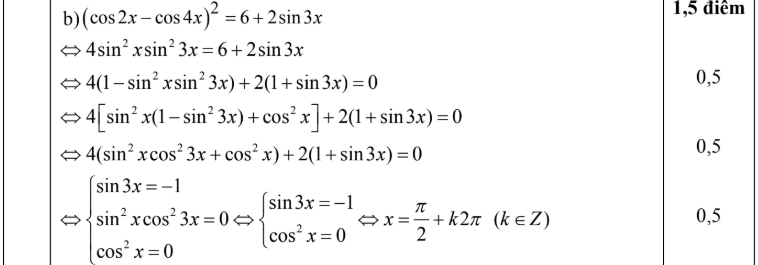
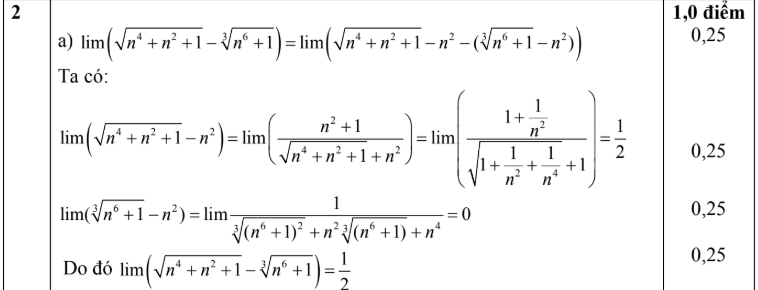
Trên đây là bộ đề thi học sinh giỏi toán 11 mà chúng tôi đem đến cho các bạn. Hi vọng với bộ đề của chúng tôi các bạn có thể luyện tập thật tốt, ôn luyện kiến thức vững chắc. Một điều nữa là bộ đề của chúng tôi có kèm theo đáp án, các bạn có thể sử dụng để so sánh kết quả một cách dễ dàng để biết mình sai ở đâu nhằm chuẩn bị tốt cho kì thi tới.




 056.3753648
056.3753648
 Chat FB
Chat FB