Tóm tắt tài liệu
Bài tập phép tịnh tiến xuất hiện trong chương phép đồng dạng và biến hình trong mặt phẳng – Hình học lớp 11. Đây là một chuyên đề khá cơ bản, tuy nhiên nguồn tài liệu chưa nhiều. Đặc biệt là về phép tịnh tiến, rất ít tài liệu nói hẵn về chuyên đề này. Đó là lý do tài liệu này được đăng tải trên website của chúng tôi. Các bạn có thể tải tài liệu về và in ra để thuận tiện hơn cho việc làm bài tập cũng như thực hành, xem công thức.
1/ LÝ THUYẾT PHÉP TỊNH TIẾN
– Trong mặt phẳng cho vectơ \[\]. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho: \[\overrightarrow{M{M}’}=\overrightarrow{v}\], được gọi là phép tịnh tiến theo vectơ \[\overrightarrow{v}\].
– Phép tịnh tiến theo vectơ không là phép đồng nhất.
– Biểu thức tọa độ của phép tịnh tiến:
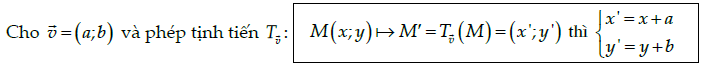
– Tính chất của phép tịnh tiến:
- Bảo toàn tính thẳng hàng và thứ tự của các điểm tương ứng.
- Biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
- Biến tam giác thành tam giác bằng nó. (trực tâm thành trực tâm, trọng tâm thành trọng tâm)
- Biến đường tròn thành đường tròn có cùng bán kính
2/ KỸ NĂNG XÁC ĐỊNH ẢNH CỦA ĐƯỜNG THẲNG QUA PHÉP TỊNH TIẾN
- Phương pháp 1: Chọn 2 điểm bất kì trên \[\Delta \] , xác định ảnh tương ứng. Đường thẳng \[\Delta \] cần tìm là đường thẳng qua hai ảnh.
- Phương pháp 2: Theo tính chất của phép tịnh tiến: Biến đường thẳng thành đường thẳng song song hoặc
trùng với nó. - Phương pháp 3: Sử dụng quĩ tích
Nhận xét: Trong 3 phương pháp trên,
+) Phương pháp 1 tỏ ra hiệu quả cho tất cả các phép biến hình (dù dài dòng).
+) Phương pháp 2 tốt vì sử dụng tính chất phép tịnh tiến.
+) Phương pháp 3 nhanh hơn, phù hợp với trắc nghiệm và việc xác định ảnh của các hình Elíp, parabol..
3/ XÁC ĐỊNH ẢNH CỦA ĐƯỜNG TRÒN
- Phương pháp 1: Theo tính chất của phép tịnh tiến: Biến đường tròn thành đường tròn có cùng bán kính.
- Phương pháp 2: Sử dụng quỹ tích
4/ SỬ DỤNG PHÉP TỊNH TIẾN GIẢI BÀI TẬP QUỸ TÍCH
Để xử lý tốt bài toán quĩ tích ta cần nắm vững một số nhận xét sau:
- Xác định các yếu tố cố định (không thay đổi), và điểm di động ban đầu.
- Biểu diễn điểm (cần tìm quỹ tích) theo điểm đi động ban đầu thông qua các yếu tố cố định.
Đây là một dạng toán khá khó, do đó các em cần có một tư duy linh động. Làm càng nhiều bài tập sẽ càng tạo nhiều tư duy cho bài tập ấy.
5/ BÀI TẬP TRẮC NGHIỆM PHÉP TỊNH TIẾN
Dưới đây là tổng hợp khác nhiều bài tập trắc nghiệm về phép tịnh tiến. Các em có thể theo dõi ngay phía bên dưới hoặc tải tài liệu về để xêm chi tiết và đầy đủ hơn nhé!
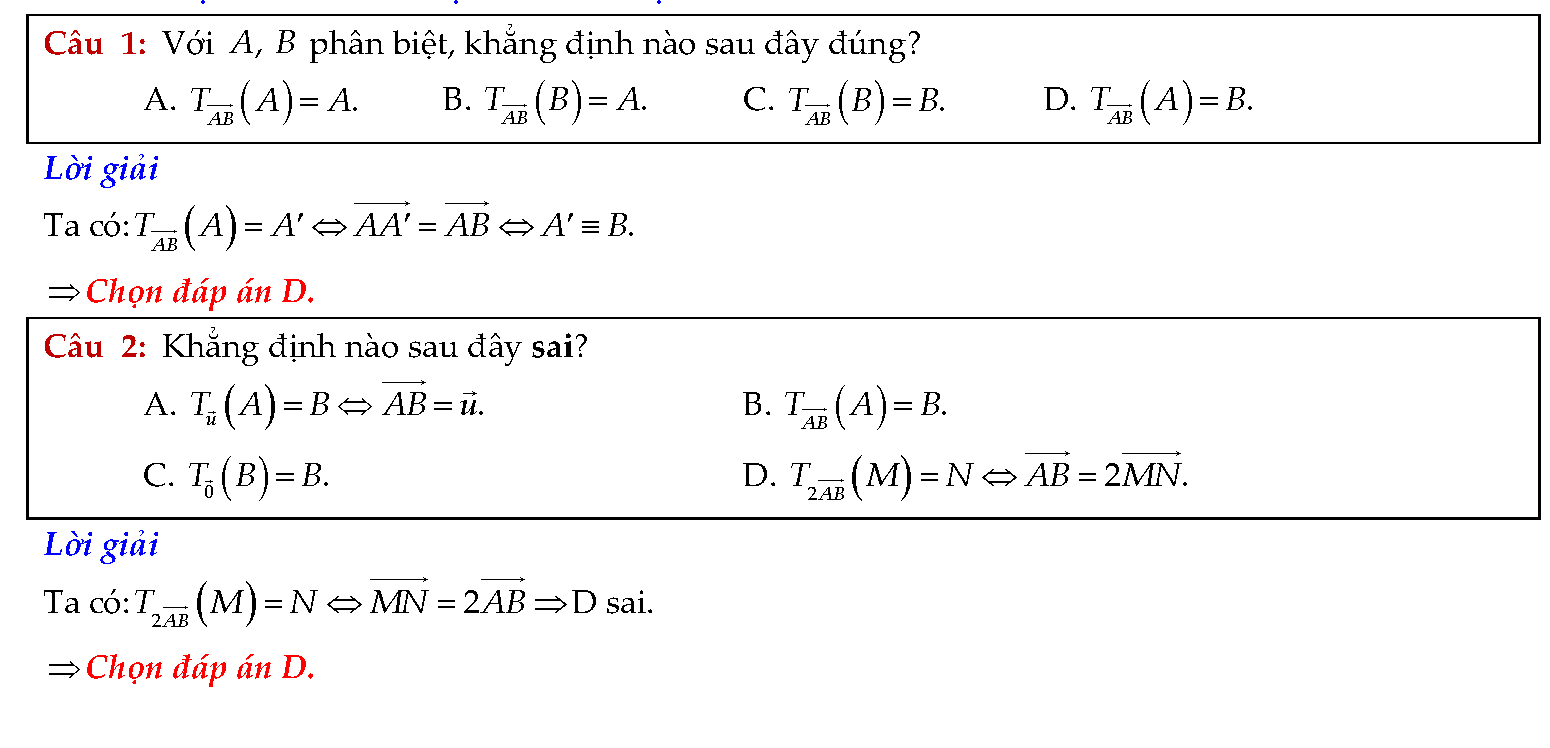

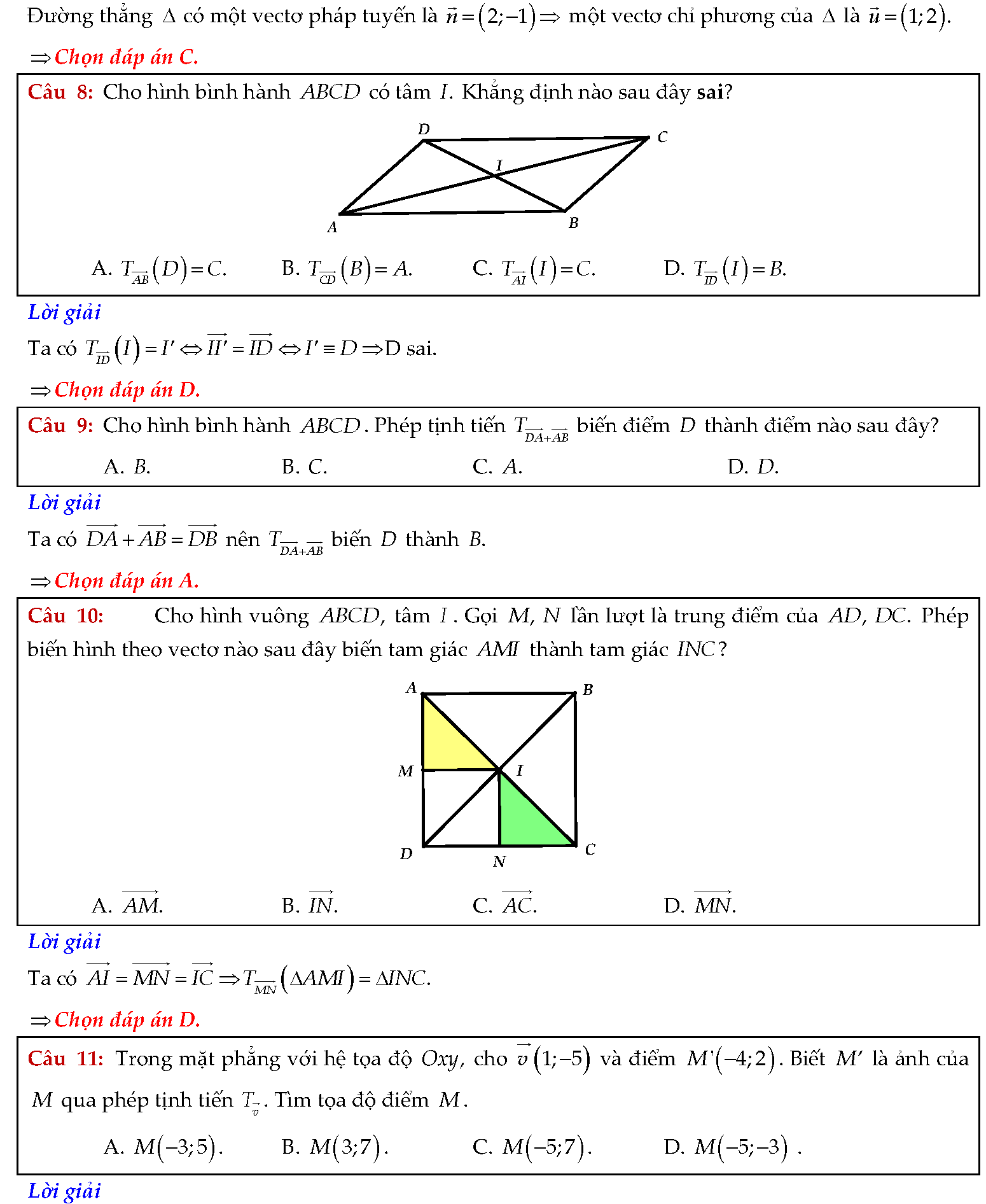



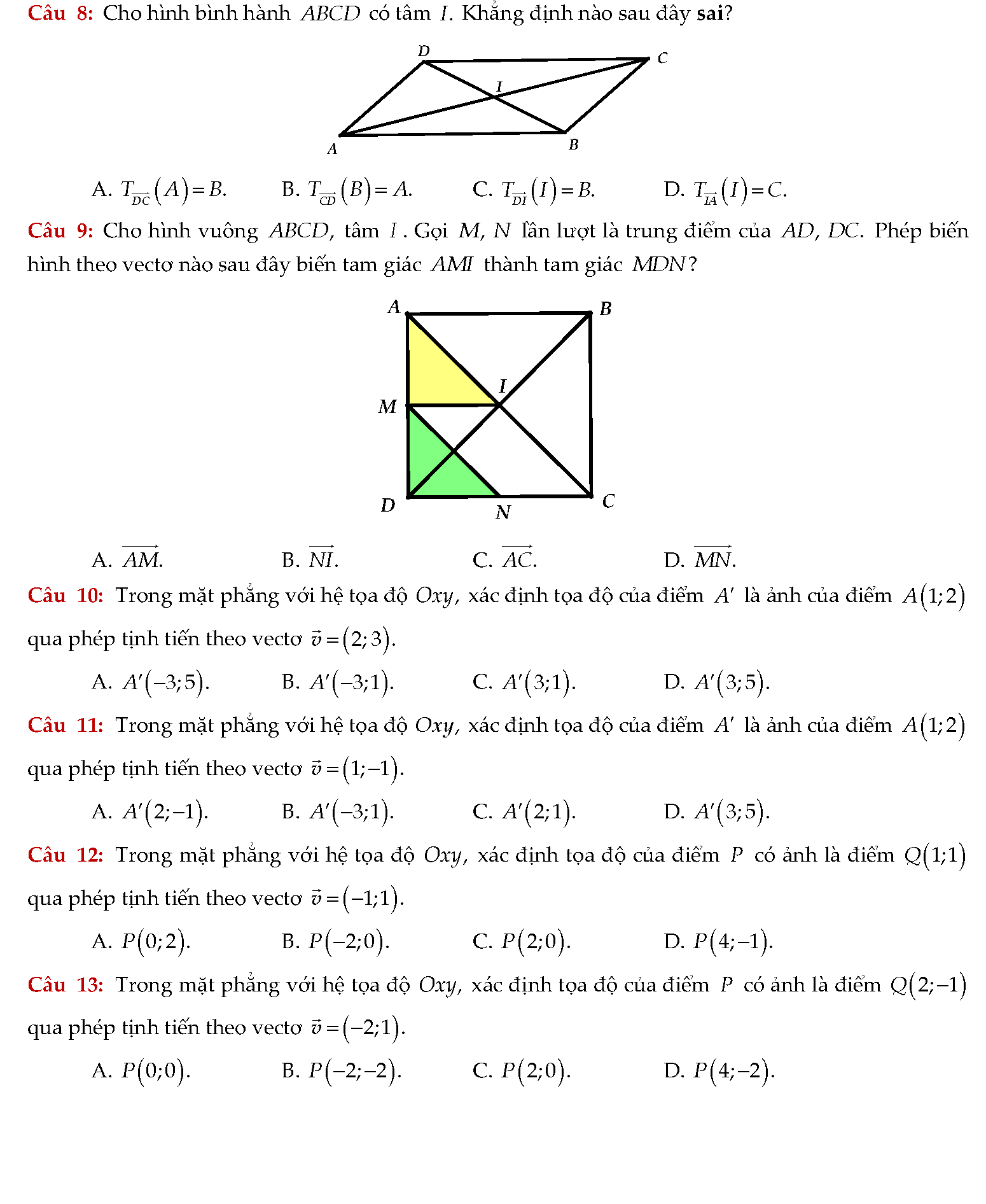
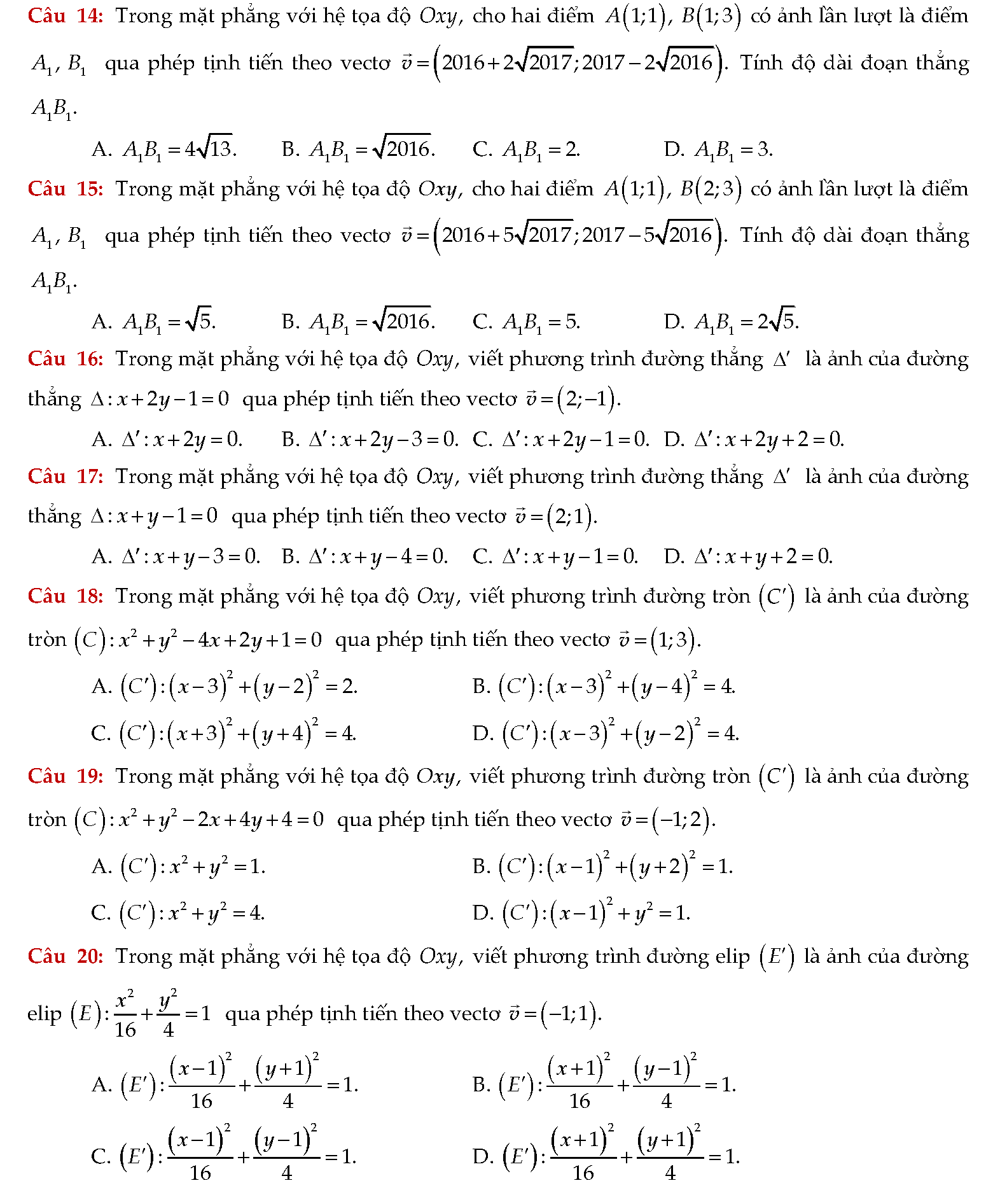

Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập phép tịnh tiến trong tài liệu trên. Để đạt được kết quả cao nhất, các em cần phải luyện tập một cách nghiêm túc. Đặc biệt cần nắm vững lý thuyết, không được nhầm lẫn giữa các công thức. Việc tự học qua những tài liệu thật sự rất có ích. Chúc các em học tốt.




 056.3753648
056.3753648
 Chat FB
Chat FB