Tóm tắt tài liệu
Bài tập hình học không gian 11 bao gồm khá nhiều dạng với một số biến thể khác nhau. Nhằm giúp các em có một nguồn tài liệu tư học phong phú, đầy đủ và rõ ràng. Chúng tôi đã tổng hợp một số bài tập hình không gian lớp 11 có lời giải chi tiết. Những bài tập dưới đây mang tính cốt lõi, đặc trưng nhất cho từng dạng toán. Do đó, đây được coi là những bài tập cơ sở giúp phát triển tư duy hình không gian của các em.
Xác định giao tuyến của hai mặt phẳng
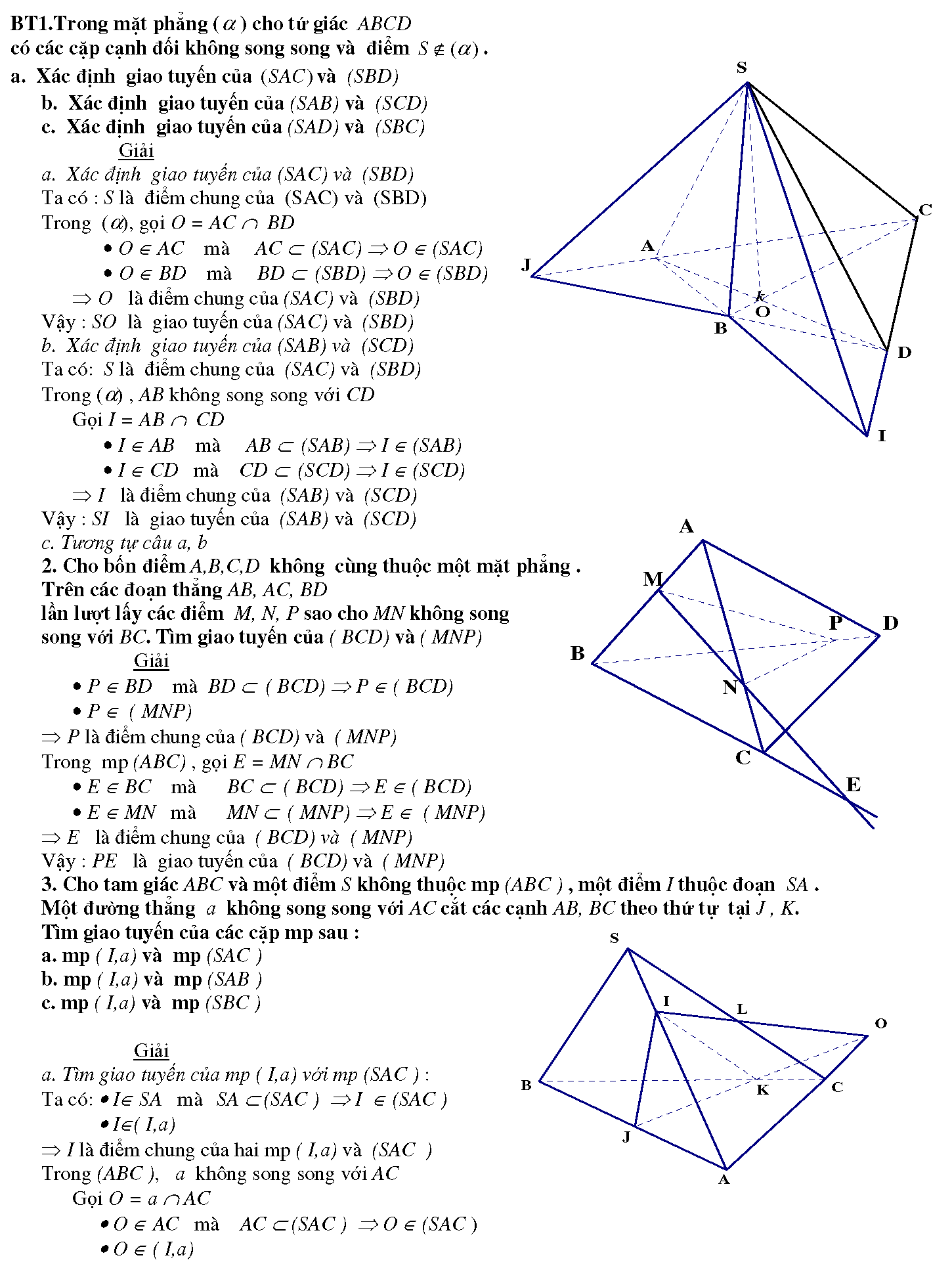
1.1. BT1.Trong mặt phẳng (a ) cho tứ giác ABCD có các cặp cạnh đối không song song và điểm S Ï(a ).
a. Xác định giao tuyến của (SAC) và (SBD)
b. Xác định giao tuyến của (SAB) và (SCD)
c. Xác định giao tuyến của (SAD) và (SBC)
1.2. Cho bốn điểm A,B,C,D không cùng thuộc một mặt phẳng. Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của ( BCD) và ( MNP).
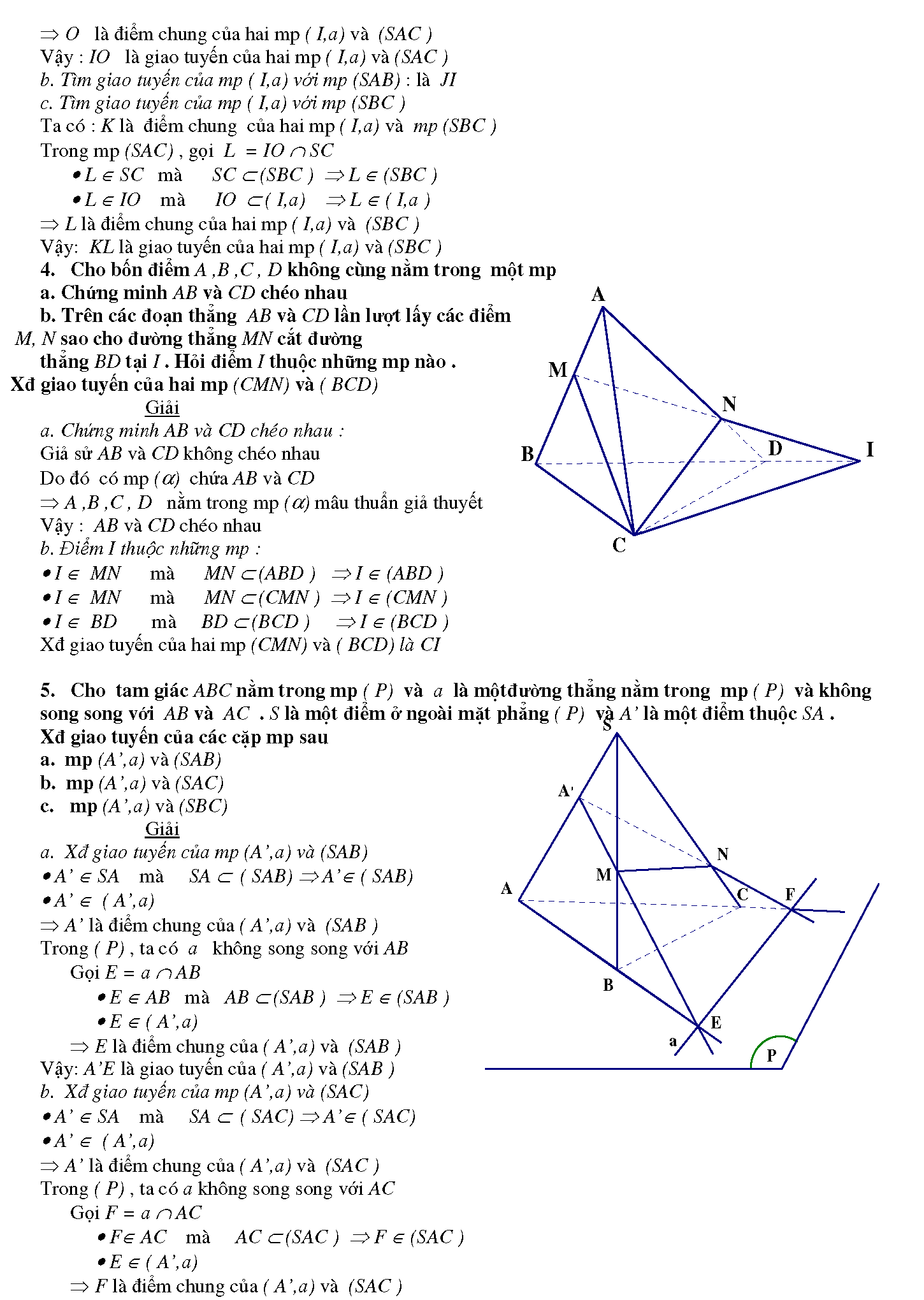
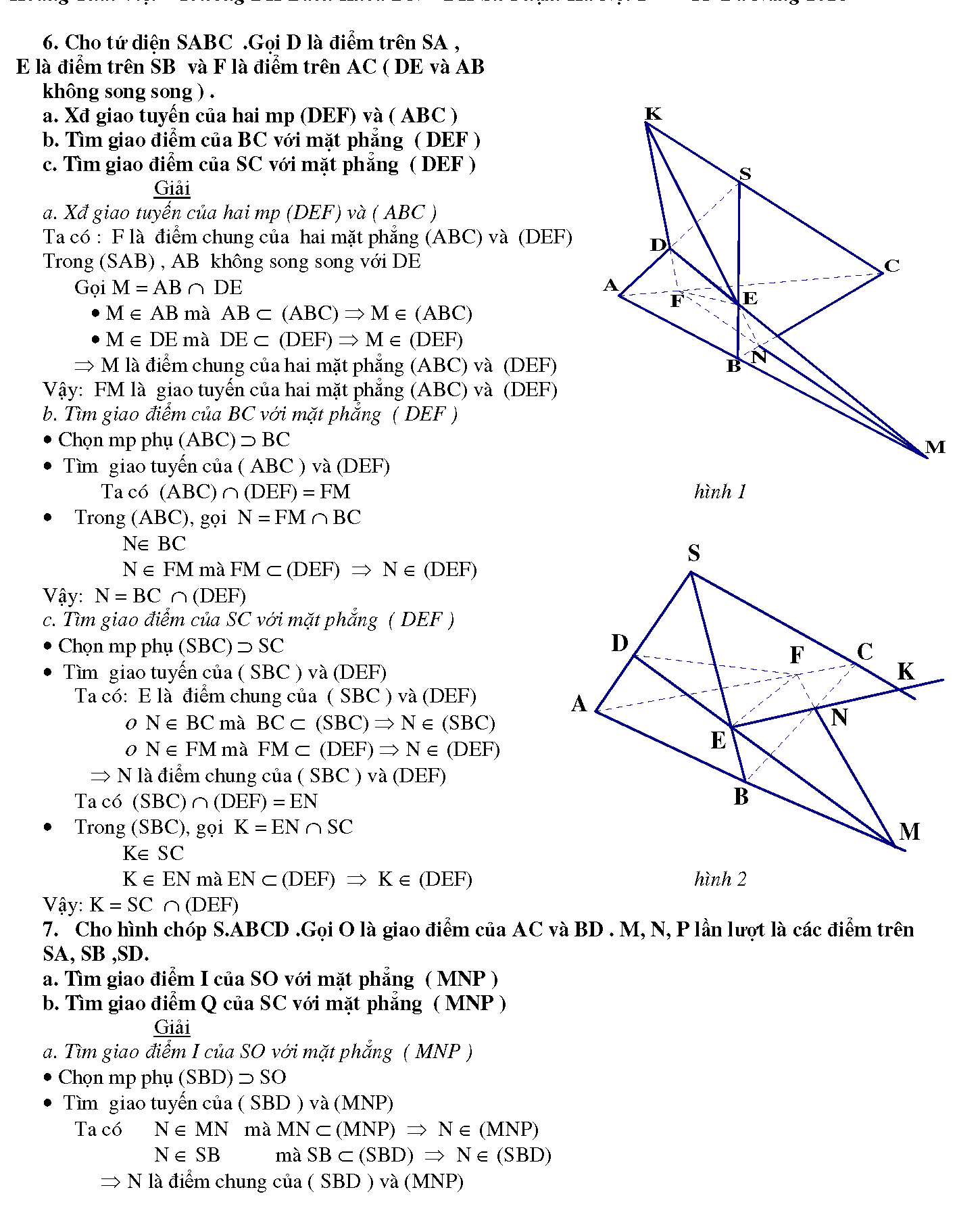
1.3. 4. Cho bốn điểm A ,B ,C , D không cùng nằm trong một mặt phẳng:
a. Chứng minh AB và CD chéo nhau
b. Trên các đoạn thẳng AB và CD lần lượt lấy các điểm M, N sao cho đường thẳng MN cắt đường thẳng BD tại I . Hỏi điểm I thuộc những mp nào. Xđ giao tuyến của hai mp (CMN) và ( BCD)?
Xác định giao điểm của một đường thẳng a và một mặt phẳng
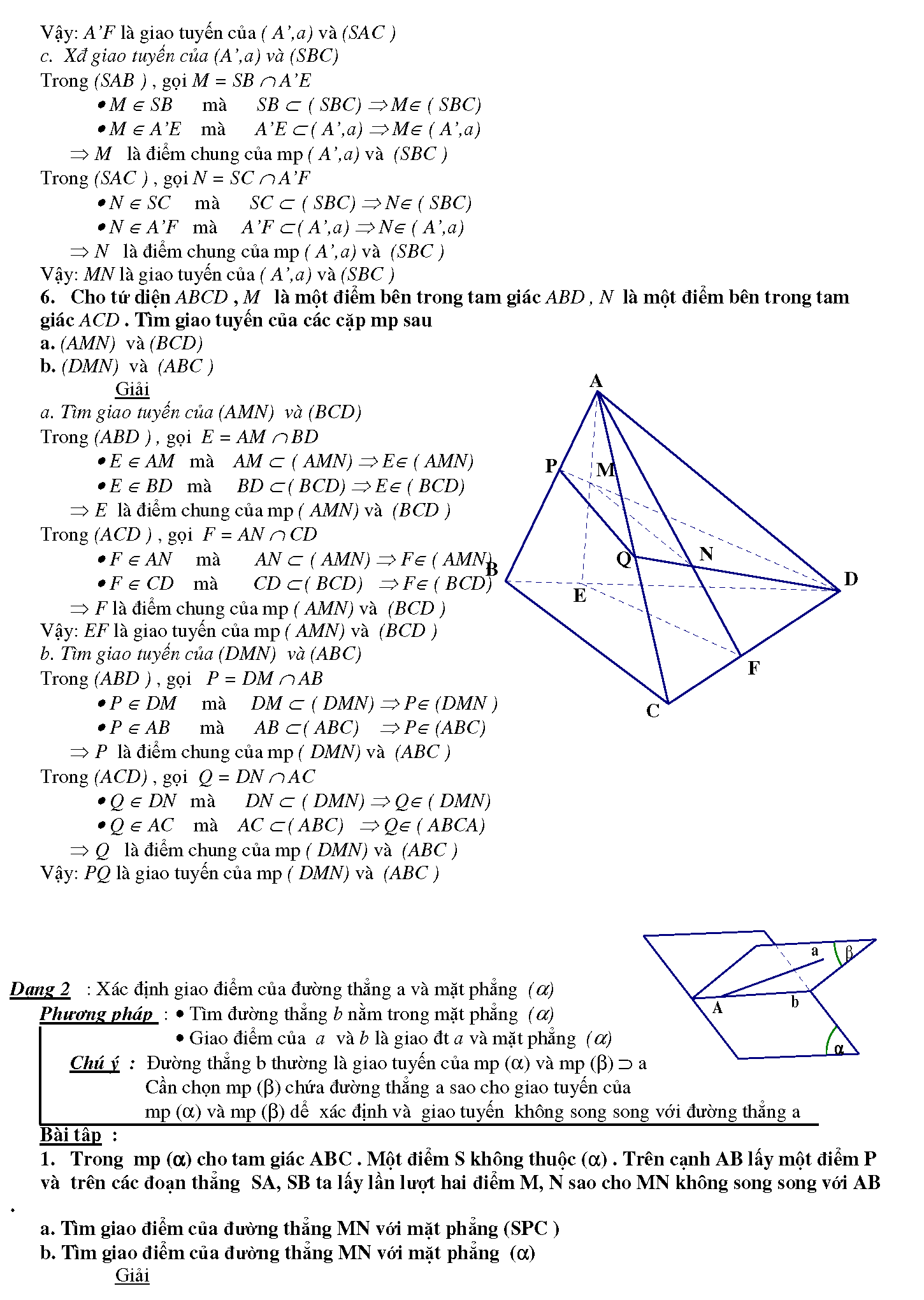
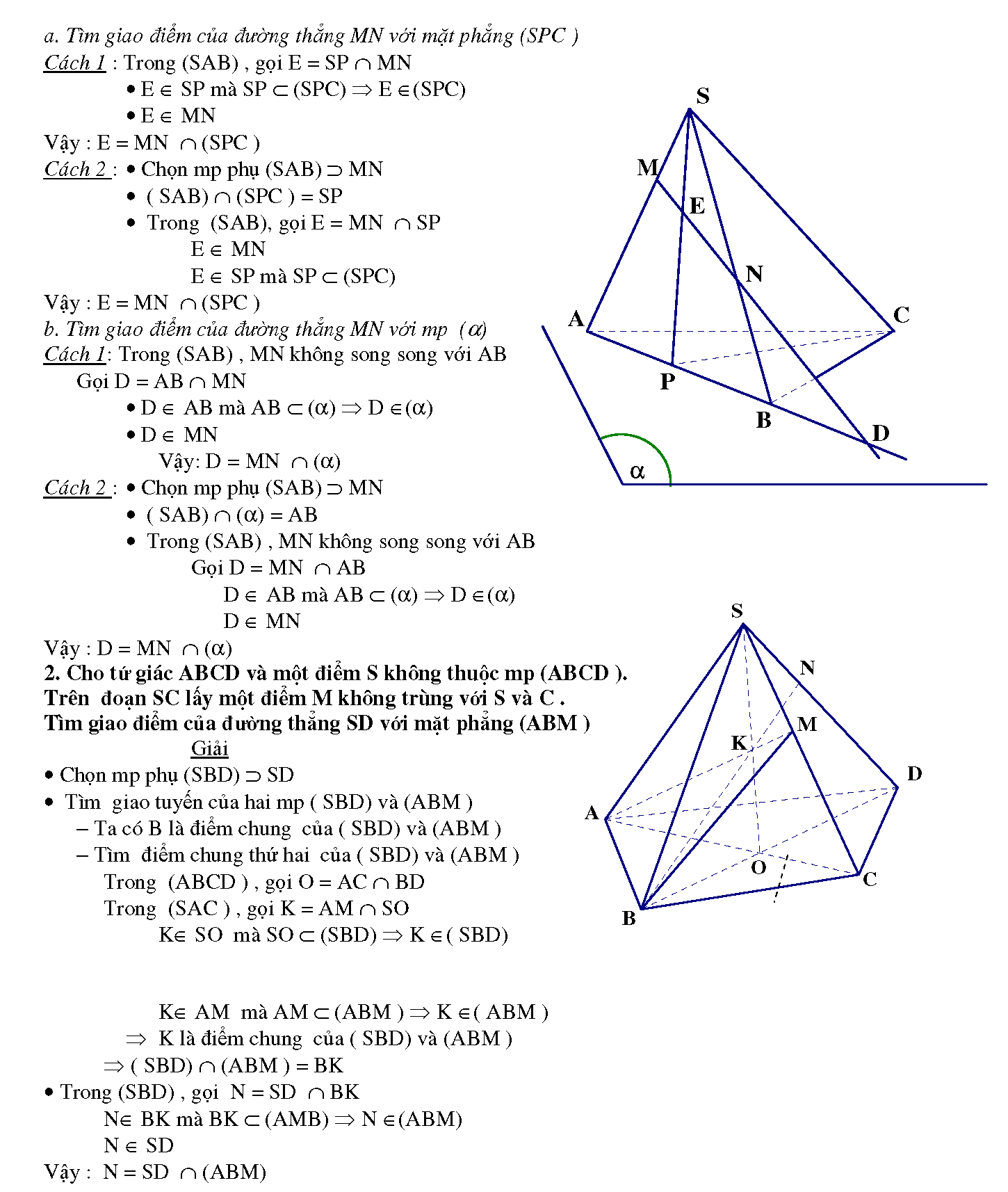
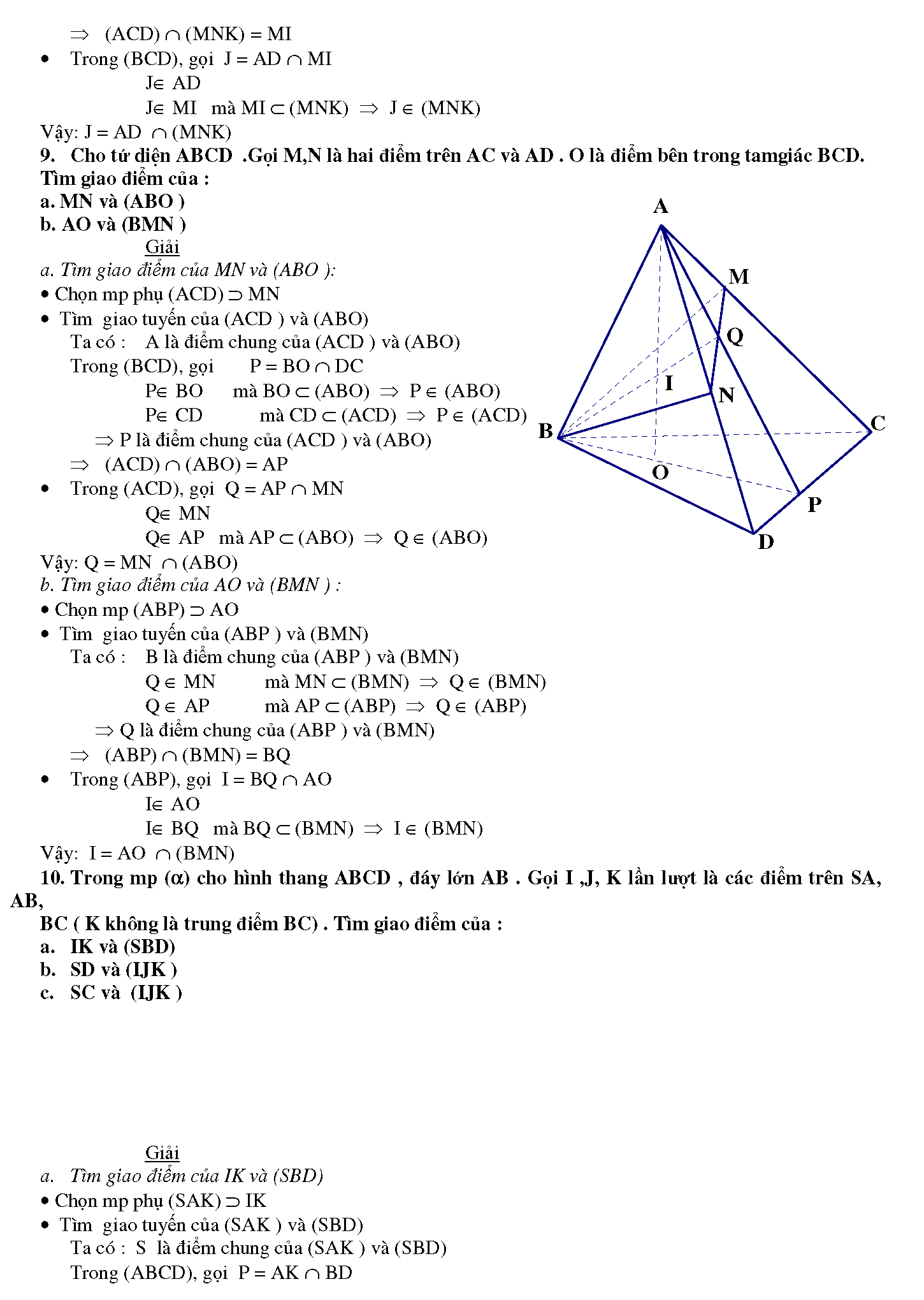
2.1. Trong mp (a) cho tam giác ABC . Một điểm S không thuộc (a) . Trên cạnh AB lấy một điểm P và trên các đoạn thẳng SA, SB ta lấy lần lượt hai điểm M, N sao cho MN không song song với AB.
a. Tìm giao điểm của đường thẳng MN với mặt phẳng (SPC )
b. Tìm giao điểm của đường thẳng MN với mặt phẳng (a)
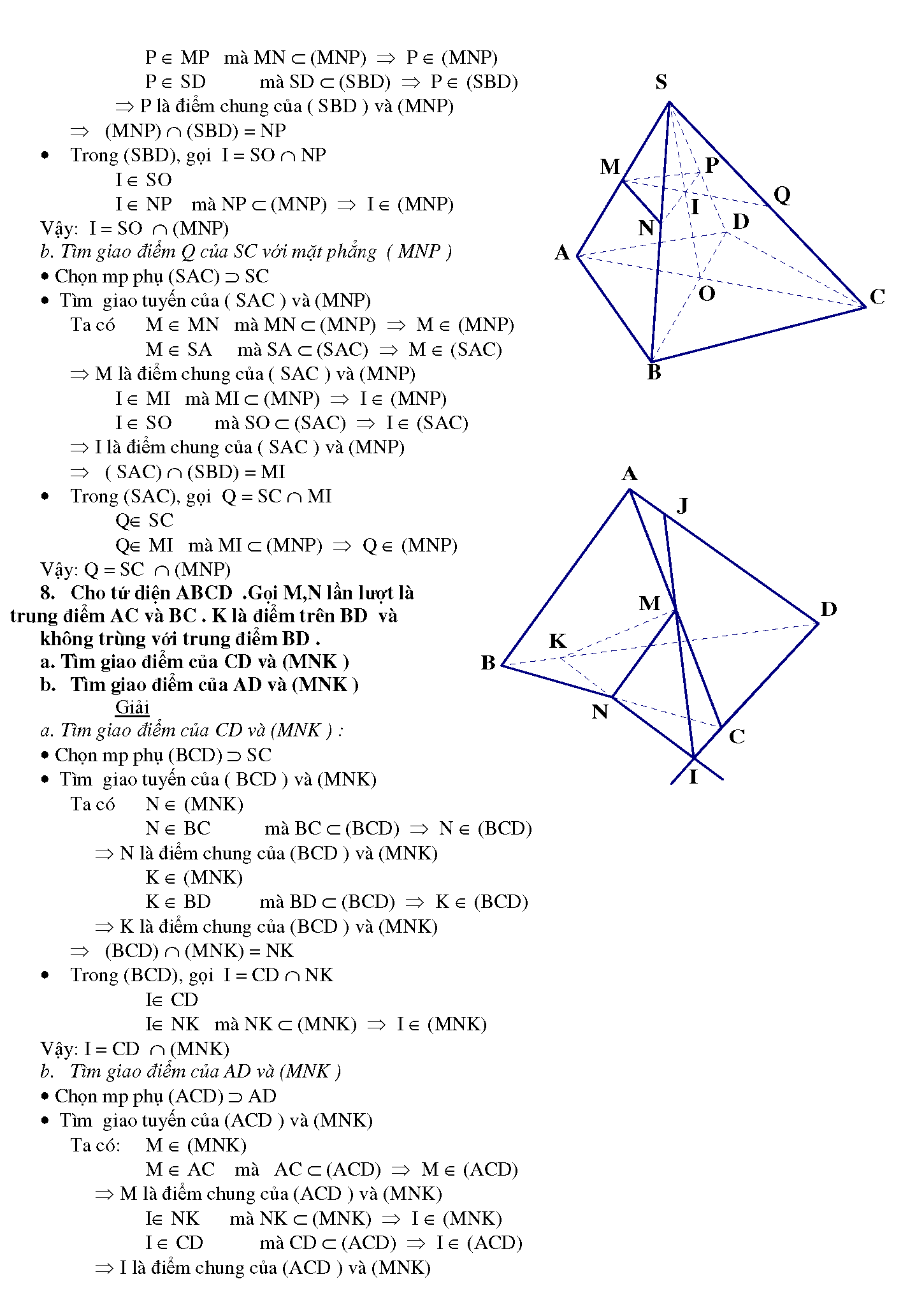
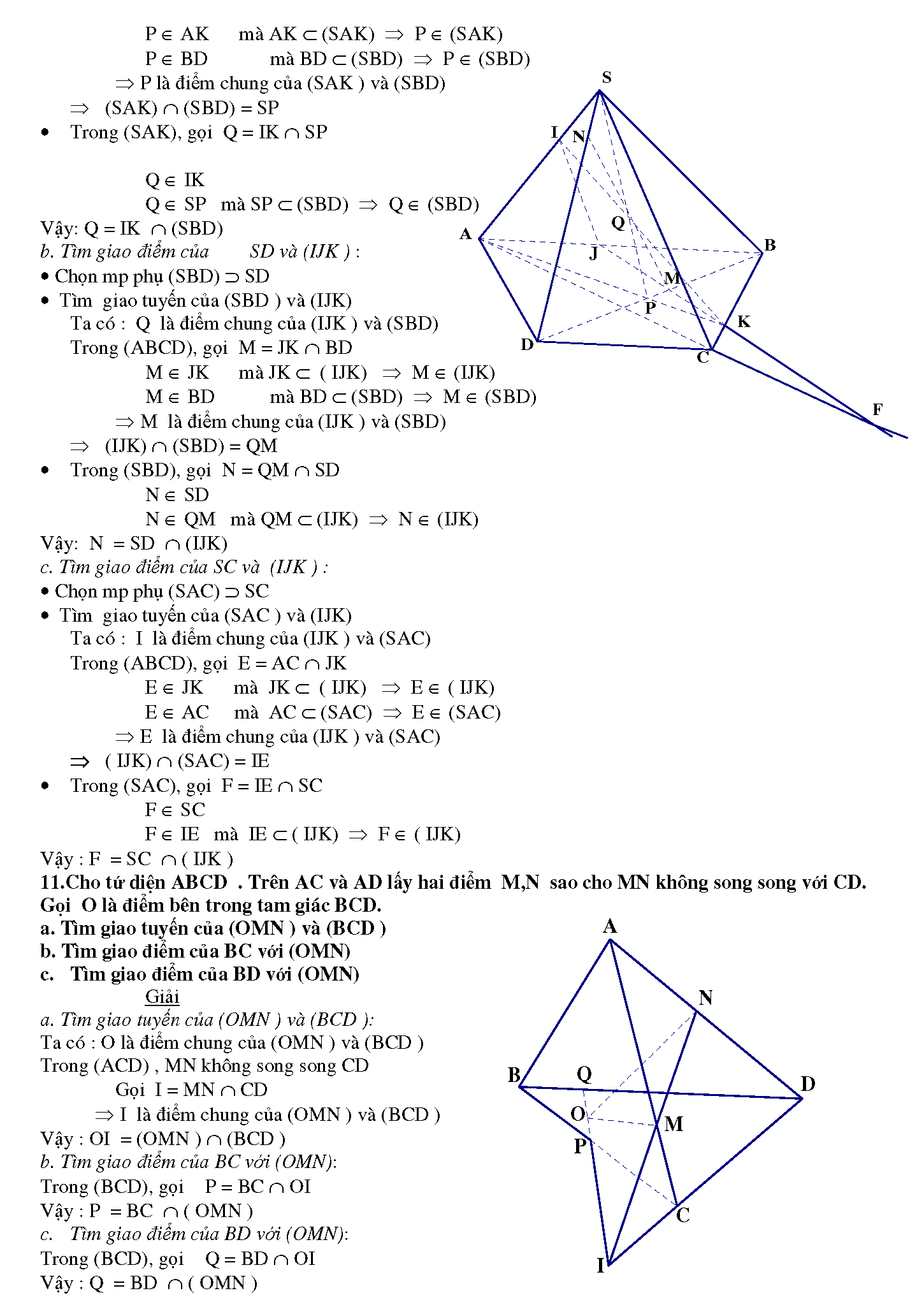
2.2. Cho tứ giác ABCD và một điểm S không thuộc mp (ABCD ). Trên đoạn SC lấy một điểm M không trùng với S và C. Tìm giao điểm của đường thẳng SD với mặt phẳng (ABM).
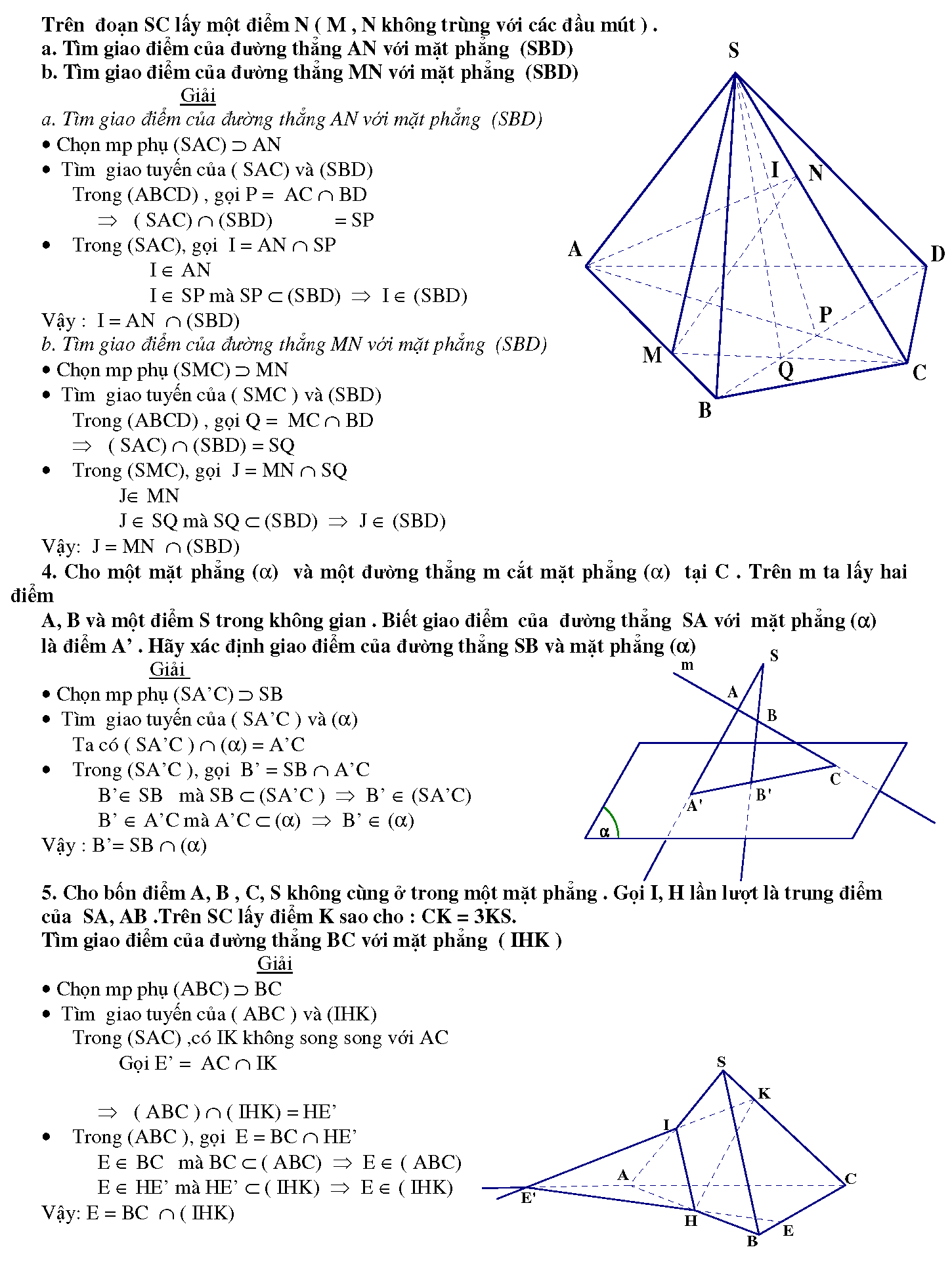
2.3. 3. Cho tứ giác ABCD và một điểm S không thuộc mp (ABCD ). Trên đoạn AB lấy một điểm M. Trên đoạn SC lấy một điểm N (M,N không trùng với các đầu mút)
a. Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD)
b. Tìm giao điểm của đường thẳng MN với mặt phẳng (SBD)
Chứng minh 3 điểm thẳng hàng
Phương pháp giải bài tập này là:
- Chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt
- Khi đó ba điểm thuộc đường thẳng giao tuyến của hai mặt phẳng
Tính thiết hiện của hình chóp và mặt phẳng
- Mặt phẳng (a ) có thể chỉ cắt một số mặt của hình chóp
- Cách 1: Xác định thiết diện bằng cách kéo dài các giao tuyến
- Cách 2: Xác định thiết diện bằng cách vẽ giao tuyến phụ
Chứng minh hai đường thẳng song song
- Chứng minh a và b đồng phẳng và không có điểm chung
- Chứng minh a và b phân biệt và cùng song song với đường thẳng thứ ba
- Chứng minh a và b đồng phẳng và áp dụng các tính chất của hình học phẳng (cạnh đối của hình bình hành , định lý talet … )
- Sử dụng các định lý
- Chứng minh bằng phản chứng
Chứng minh đường thẳng a song song với mặt phẳng (P)
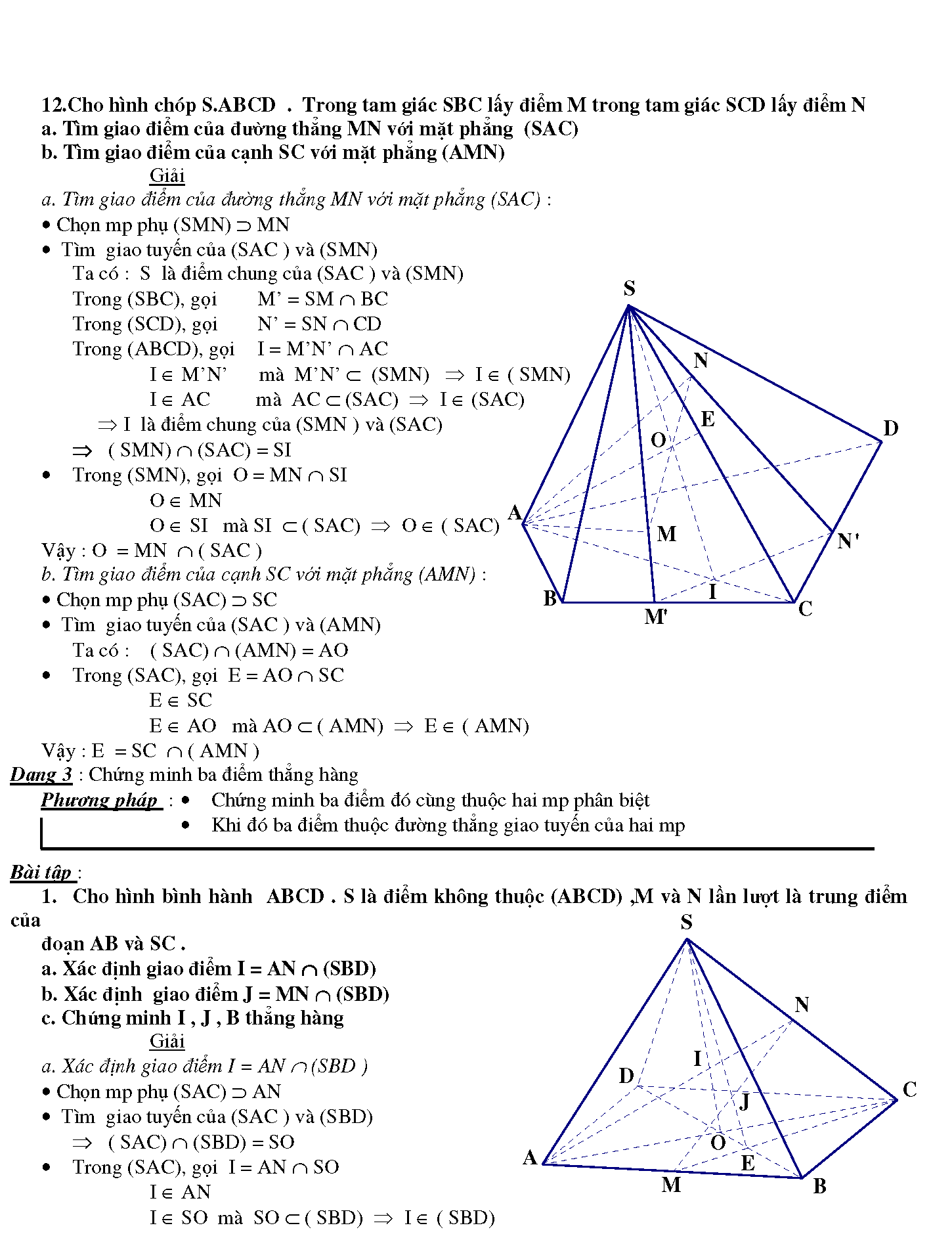
6.1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M ,N lần lượt là trung điểm các cạnh AB và CD .
a. Chứng minh MN // (SBC) , MN // (SAD)
b. Gọi P là trung điểm cạnh SA . Chứng minh SB và SC đều song song với (MNP)
c. Gọi G1 ,G2 lần lượt là trọng tâm của DABC và DSBC. Chứng minh G1G2 // (SAB)
Chứng minh hai mặt phẳng song song với nhau
7.1. Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA ,SD
a. Chứng minh rằng : (OMN) // (SBC)
b. Gọi P, Q , R lần lượt là trung điểm của AB ,ON, SB. Chứng minh : PQ // (SBC), (MOR) // (SCD)
Tổng hợp bài tập hình học không gian lớp 11
Cảm ơn các em đã xem và tải tài liệu Bài tập hình học không gian 11. Đây là một chuyên đề không quá khó, nhưng nó tạo nền tảng cho các em học hình không gian lớp 12. Do đó, cần phải học một cách kĩ lưỡng, khoa học nhất. Các bài toán thường khá logic về mặt tư duy nên các em phải nắm được. Chúc các em học tốt.



 056.3753648
056.3753648
 Chat FB
Chat FB