Tóm tắt tài liệu
Ở bài viết này sẽ giới thiệu đến các em các chủ đề kiến thức để giải bài tập đạo hàm như sau: Công thức tính đạo hàm, đạo hàm cơ bản, bài tập đạo hàm lượng giác và hơn 20 tài liệu về các bài tập trong chuyên đề.
Bảng công thức đạo hàm (pdf): CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆU >> Hướng dẫn tải
520 bài tập trắc nghiệm đạo hàm có đáp án và lời giải chi tiết: CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆU
1. Công thức tính đạo hàm
a) Qui tắc tính đạo hàm
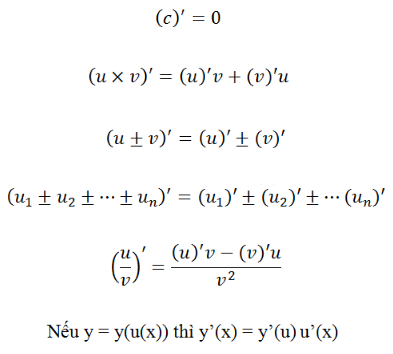
b) Công thức tính đạo hàm với biến số
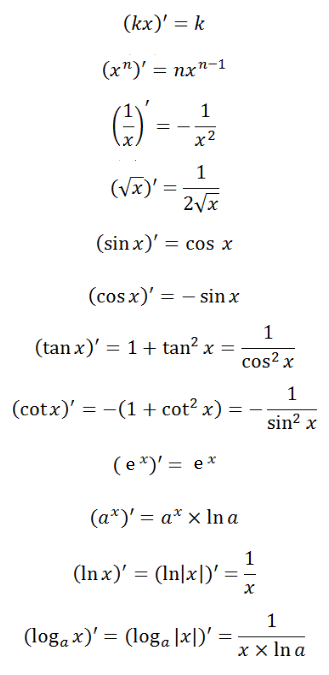
c) Đạo hàm của hàm số hợp
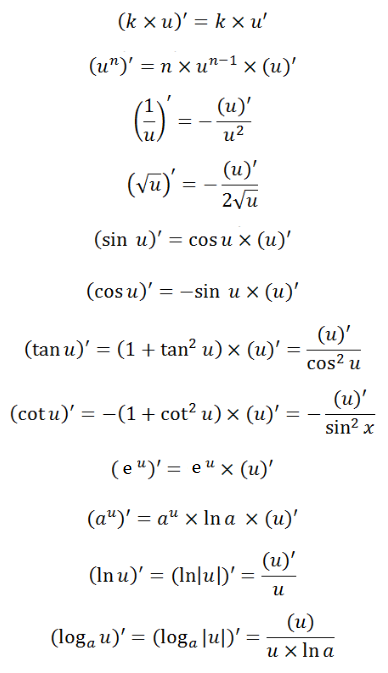
d) Đạo hàm của hàm phân thức
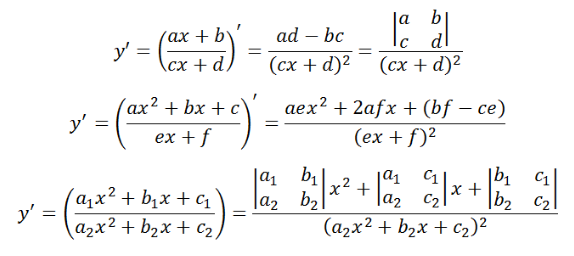
2. Các dạng toán đạo hàm cơ bản
Dạng 1: Tính đạo hàm của hàm số
+ Phương pháp: Ta vận dụng các qui tắc và phép tính đạo hàm, đặc biệt là đạo hàm của hàm hợp. Nếu đề yêu cầu tính đạo hàm tại một điểm ta cần tính đạo hàm rồi thay vào để được kết quả.
Ví dụ 1: Tính các đạo hàm của các hàm số sau
a) \[y={{x}^{3}}-2{{x}^{2}}+3x+4\]
b) \[y=\sin x-\cos x+\tan x\]
c) \[y={{x}^{4}}+2\sqrt{x}\]
d) \[y=\cot x-3x+2\]
Đáp án:
a) Ta có: \[{y}’=({{x}^{3}}-2{{x}^{2}}+3x+4)=3{{x}^{2}}-4x+3\]
b) Ta có: \[{y}’=(\sin x-\cos x+\tan x)=\cos x+\sin x+\frac{1}{{{\cos }^{2}}x}\]
c) Ta có: \[{y}’=({{x}^{4}}+2\sqrt{x}{)}’=4{{x}^{3}}+\frac{1}{\sqrt{x}}\]
d) Ta có: \[{y}’=(\cot x-3x+2{)}’=-\frac{1}{{{\sin }^{2}}x}-3\]
Ví dụ 2: Tính các đạo hàm của các hàm số sau tại các điểm tương ứng
a) \[y=-{{x}^{3}}+3{{x}^{2}}-4x+1,{{x}_{0}}=-1\]
b) \[y=\sin 2x+\cos x,{{x}_{0}}=-\frac{\pi }{4}\]
c) \[y=\sqrt{x}-2x,{{x}_{0}}=2\]
Đáp án:
a) Ta có: \[{y}’=(-{{x}^{3}}+3{{x}^{2}}-4x+1)=-3{{x}^{2}}+6x-4\]
Suy ra: \[{y}'(-1)=-3-6-4=-13\]
b) Ta có: \[{y}’=(\sin 2x+\cos x{)}’=2\cos 2x-\sin x\]
Suy ra: \[{y}’\left( -\frac{\pi }{4} \right)=2\cos \left( -\frac{\pi }{2} \right)-\sin \left( -\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}\]
c) Ta có: \[{y}’=(\sqrt{x}-2x{)}’=\frac{1}{2\sqrt{x}}-x\]
Suy ra: \[{y}’\left( 2 \right)=\frac{1}{2\sqrt{2}}-2=\frac{1-4\sqrt{2}}{2\sqrt{2}}\]
Dạng 2: Giải phương trình y’=0
Ví dụ 1: Gải phương trình y’=0 biết
a) \[y=\frac{{{x}^{2}}}{x-1}\]
b) \[y={{x}^{3}}-3{{x}^{2}}\]
c) \[y=4{{x}^{3}}-12{{x}^{2}}+9x-1\]
d) \[y=\frac{{{x}^{2}}+2x+2}{x+1}\]
e) \[y=\frac{{{x}^{2}}+3x+3}{x+1}\]
f) \[y=\frac{{{x}^{4}}}{2}-3{{x}^{2}}+\frac{5}{2}\]
g) \[y=-{{x}^{4}}-2{{x}^{2}}+3\]
h) \[y=\frac{{{x}^{2}}+x+2}{x-1}\]
i) \[y=\frac{2{{x}^{2}}+x}{x+1}\]
3. Bài tập đạo hàm lượng giác


4. Bài tập tự luận, trắc nghiệm đạo hàm
CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆU >> Hướng dẫn tải
Cảm ơn các em đã xem và tải các tài liệu trên. Để xem nhiều tài liệu hơn nữa về chuyên đề đạo hàm cũng như công thức đạo hàm, các em có thể truy cập tại đây: https://tailieure.com/tag/dao-ham




 056.3753648
056.3753648
 Chat FB
Chat FB