Đề thi HSG toán 10 – Tổng hợp hơn 30 đề thi có lời giải

Dưới đây là tài liệu tổng hợp hơn 30 đề thi HSG toán 10 đã diễn ra vào các năm học trước từ một số trường THPT trên cả nước. Đối với nhiều em học sinh thì đây là một kì thi khá quan trọng, qua kì thi các em có thể chứng minh được năng lực cũng như niềm đam mê đối với môn học này. Dưới đây là tổng hợp các đề thi có lời giải cực hay mà tailieure.com đã tổng hợp lại. Chúc các em ôn luyện thật tốt!

TẢI XUỐNG PDF ↓

Danh sách đề thi HSG toán 10

1. Đề thi học sinh giỏi toán 10 cấp thành phố

2. Đề thi học sinh giỏi toán 10 cấp trường

3. Đề thi học sinh giỏi toán 10 có đáp án cấp tỉnh

4. Đề thi học sinh giỏi toán 10 Violympic

5. Đề thi olympic toán học 30/4 Lê Hồng Phong

Chủ đề thi học sinh giỏi toán lớp 10

1. Bài toán liên quan đến tương giao đồ thị dạng nâng cao.

2. Giải bất phương trình hay lạ khó

3. Giải phương trình hay lạ khó

4. Giải bất đẳng thức hay lạ khó

5. Giải hệ phương trình hay lạ khó, nâng cao, phát triển

6. Bài toán nâng cao trong hệ tọa độ Oxy, đường tròn (C) và điểm cố định. Bài toán kết hợp với tiếp tuyến

7. Bất đẳng thức cực khó liên quan đến các bất đẳng thức dạng cổ điển.

8. Tính giá trị của biểu thức lượng giác phức tạp

9. Bài toán liên quan đến vecto hay lạ khó

10. Tìm m để bất phương trình sau có nghiệm, vô nghiệm, vô số nghiệm…

Một số bài toán khó trong các đề thi học sinh giỏi

Bài 1:

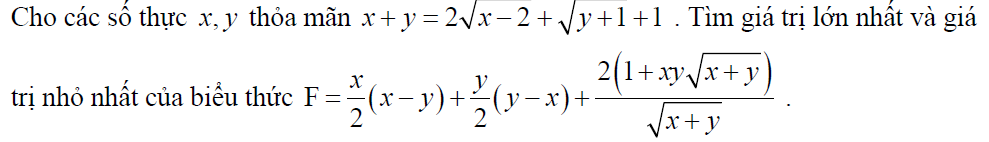
Bài 2:

Phân dạng đề thi hsg môn toán

Dạng 1: Tương giao đồ thị hàm số

Cho Parabol (P) : y = x2 + 2mx + 3 và đường thẳng (d) : y = 2x −1. Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B thỏa mãn AB = 10.

Dạng 2: Giải phương trình, hệ phương trình, bất phương trình

Giải các bất phương trình sau: \[\frac{x+2}{\sqrt{2({{x}^{4}}-{{x}^{2}}+1)}-1}\ge \frac{1}{x-1}\]

Dạng 3: Mặt phẳng tọa độ

1. Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm A(2;0) và đường tròn (C) : x2 + y2 + 2x − 6y + 2 = 0 . Tìm điểm M trên trục hoành sao cho từ M kẻ được hai tiếp tuyến MB, MC với đường tròn (B và C là các tiếp điểm) sao cho BC đi qua A.

2. Cho tam giác ABC có BC = 2, A = 60 và hai đường trung tuyến BM, CN vuông góc với nhau. Tính diện tích tam giác ABC.

3. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có tâm I. Trung điểm cạnh AB là M(0;3) , trung điểm đoạn CI là J(1;0) . Tìm tọa độ các đỉnh của hình vuông, biết đỉnh D thuộc đường thẳng Δ : x − y +1 = 0.

Ví dụ 2:
Trong mặt phẳng tọa độ 0xy cho tam giác ABC vuông tại B, AB = 2BC, D là trung điểm AB, E là điểm thuộc đoạn AC sao cho AC = 3EC, có phương trình CD: x = 3y + 1

a) Chứng minh rằng BE là phân giác trong của góc B, Tìm tọa độ điểm I là giao của CD và BE.

b) Tìm tọa độ các đỉnh A, B, C, biết A có tung độ âm.

Dạng 3: Bài toán lãi suất

Câu 1: Một hộ nông dân dự định trồng đậu và cà trên diện tích 800m2 . Biết rằng cứ 100m2 trồng đậu cần 10 công và lãi 7 triệu đồng còn 100m2 trồng cà cần 15 công và lãi 9 triệu đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được tiền lãi cao nhất khi tổng số công không vượt quá 90.

Câu 2: Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Để sản xuất 1 tấn sản phẩm loại I cần máy thứ nhất làm việc trong 3 giờ và máy thứ hai làm việc trong 1 giờ. Để sản xuất 1 tấn sản phẩm loại II cần máy thứ nhất làm việc trong 1 giờ và máy thứ hai làm việc trong 1 giờ. Mỗi máy không đồng thời làm hai loại sản phẩm cùng lúc. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai làm việc không quá 4 giờ. Hỏi một ngày nên sản xuất bao nhiêu tấn mỗi loại sản phẩm để tiền lãi lớn nhất?

Vậy là chúng ta vừa tìm hiểu xong khá nhiều đề thi HSG toán 10. Nếu có bất kì thắc mắc về lời giải cũng như phương pháp giải bài tập. Các em đừng ngần ngại mà hãy để lại bình luận dưới bài viết này. Đây là bộ tài liệu hay nhất mà chúng tôi có được từ năm 2018. Một số đề thi học sinh giỏi toán lớp 10 sẽ liên tục được cập nhật từ những năm sau.