Tóm tắt tài liệu
Hệ thức lượng trong tam giác lớp 10 thuộc bài 3 chương 2 tích vô hướng của hai véc tơ và ứng dụng. Bài viết này sẽ giới thiệu cho các em một số công thức trong tam giác và các hệ thức lượng tương ứng. Ngoài ra còn khá nhiều bài tập hay có lời giải được đưa vào tài liệu. Các dạng bài tập chủ yếu như:
- Giải tam giác (tìm các yếu tố còn thiếu trong tam giác)
- Tính độ dài đường trung tuyến trong tam giác
- Tính độ dài đường trung trực trong tam giác
- Chứng minh các biểu thức lượng giác
Hệ thức lượng trong tam giác lớp 10 – 3 tài liệu hay nhất
Lý thuyết và bài tập ứng dụng hệ thức lượng trong tam giác
Tổng hợp các dạng bài tập về hệ thức lượng – book math
1.3: 35 bài tập có lời giải về giải tam giác
Tổng hợp lý thuyết
Định lí hàm sin và cosin trong tam giác
Cho tam giác ABC có a,b,c lần lượt là 3 cạnh đối diện của 3 góc A,B,C. R là bán kình đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC thì ta có:
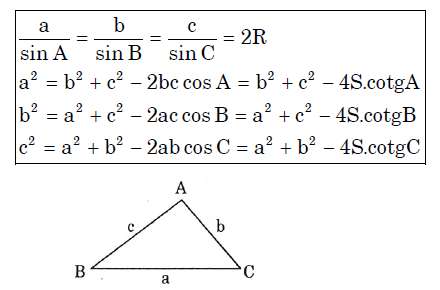
Công thức tính độ dài đường trung tuyến
Cho tam giác ABC có đường trung tuyến AM thì:
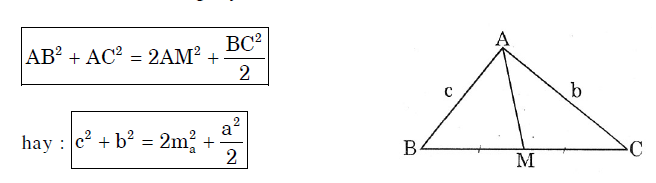
Công thức tính diện tích tam giác
Gọi:
- S là diện tích của tam giác ABC
- R là bán kính đường tròn ngoại tiếp tam giác ABC
- r là bán kính đường tròn nội tiếp tam giác ABC
- p là nửa chu vi của tam giác ABC
Ta có một số công thức tính diện tích như sau:

Các dạng toán giải tam giác
- Giải tam giác khi biết một cạnh và hai góc: Dạng bài này ta dùng định lí sin để tính 2 cạnh còn lại
- Giải tam giác khi biết hai cạnh và góc xen giữa: Dạng bài này ta dùng định lí cosin để tính cạnh thứ 3
- Giải tam giác khi biết ba cạnh: Dạng này ta dùng định lí cosin để tính góc
Lưu ý cho dạng bài tập này: Một tam giác giải được khi biết 3 cạnh của nó, trong đó phải có ít nhất một yếu tố là độ dài. Việc giải tam giác được ứng dụng mạnh mẽ vào thực tế, đặc biệt là trong quá trình đo đạc, tính toán các hình học có ý nghĩa quan trọng. Ta cùng tìm hiểu qua một số bài tập như sau:


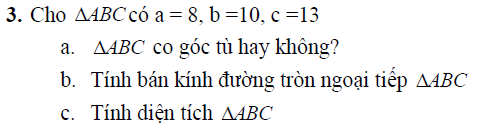

![]()
![]()
![]()
![]()
![]()
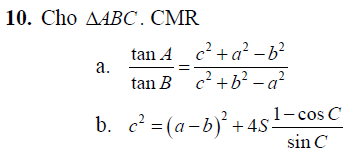
Bài tập hệ thức lượng nâng cao
- Chứng minh một đẳng thức lượng giác
- Tính giá trị của biểu thức
- Chứng minh đẳng thức lượng giác suy từ đẳng thức
- Chứng minh biểu thức lượng giác không phụ thuộc vào biến số
- Chứng minh đẳng thức lượng giác trong tam giác
- Chứng minh bất đẳng thức lượng giác
- Nhận dạng tam giác và tính các góc trong tam giác

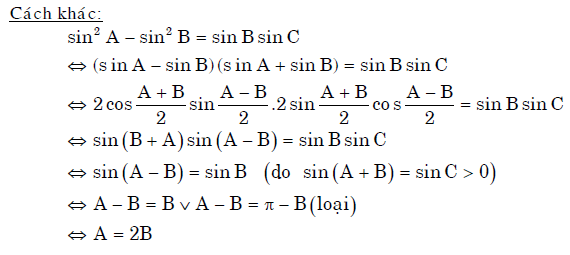
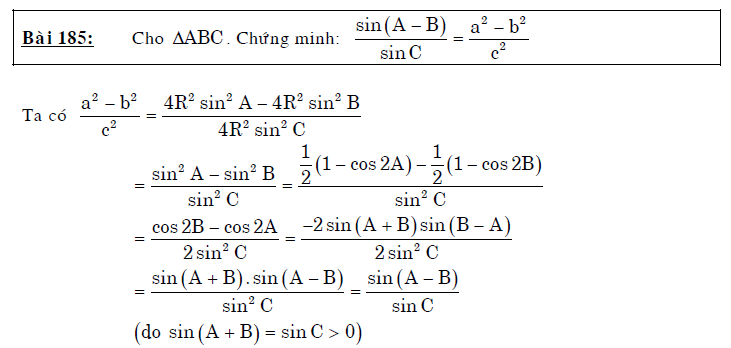
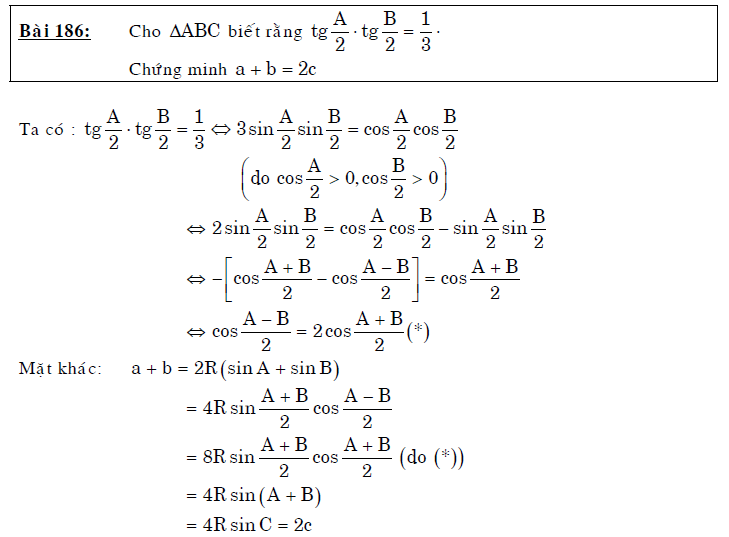

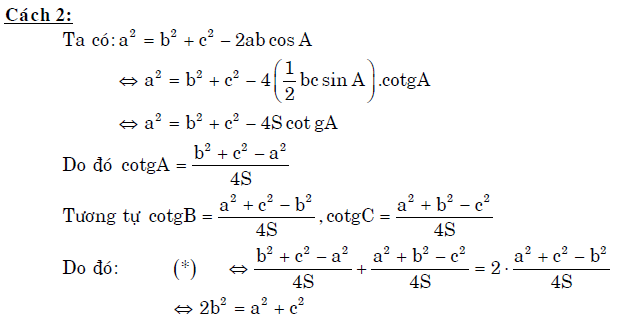

Vậy là vừa rồi chúng ta vừa tìm hiểu xong hàng loạt công thức và bài tập về hệ thức lượng trong tam giác lớp 10. Đó là những công thức cực kì quan trọng không chỉ áp dụng trong toán học mà còn có thể giải quyết các vấn đề đo đạc trong thực tế. Có thể nói, bài tập phần giải tam giác và chứng minh các đẳng thức trong tam giác mang lại ý nghĩa thực tiễn lớn nhất. Vì thế, các bài toán thực tế trong đề thi THPT quốc gia cũng khá hay ra lại các dạng bài tập này.
Xem thêm video
Từ khóa:
- các hệ thức lượng trong tam giác và giải tam giác
- hệ thức lượng trong tam giác đều
- hệ thức lượng trong tam giác lớp 8
- công thức lượng giác
- cách nhớ hệ thức lượng trong tam giác vuông
- công thức tỉ số lượng giác trong tam giác vuông
- ứng dụng các hệ thức lượng trong tam giác
- tam giác thường



 056.3753648
056.3753648
 Chat FB
Chat FB