Tóm tắt tài liệu
Kì thi học sinh giỏi là kì thi quan trọng đối với mỗi học sinh. Dưới đây là đề thi hsg toán 12 mà chúng tôi xin gửi đến các bạn, hi vọng sẽ giúp các bạn kiểm tra lại, đánh giá kiến thức của mình và có thêm thời gian chuẩn bị ôn tập cho kì thi sắp tới được tốt hơn.
Danh sách nguồn của các đề
- Đề thi học sinh giỏi toán 12 của Sở giáo dục và đào tạo gia lai
- Đề thi hsg toán lớp 12 sở giáo dục và đào tạo đồng tháp
- Đề thi hsg toán trường thpt nga sơn
Cấu trúc của các đề
Mỗi đề thi sẽ bao gồm từ 4 đến 6 câu hỏi tự luận. Các câu hỏi mang tính nâng chất phân loại học sinh. Mặc dù các đề thi học sinh giỏi được trích từ nhiều năm trước nhưng lượng kiến thức vẫn thường được sử dụng trong những kì thi gần đây. Tức các đề thi luôn được cập nhật khá chi tiết.
Đề thi học sinh giỏi toán học lớp 12 tổng hợp kiến thức
Câu 1: Câu hỏi liên quan hình chóp – hình học không gian
Cho hình chóp S.ABC có các cạnh bên SA = a, SB = b, SC = c không đổi và các góc BSC [ = α, CSA [ = β, ASB [ = γ thay đổi (00 < α, β, γ < 1800, α + β + γ < 3600 và mỗi góc nhỏ hơn tổng hai góc còn lại).
a) Tính thể tích VS.ABC của hình chóp theo a, b, c, α, β, γ.
b) Chứng minh rằng khi các góc α, β, γ thay đổi, ta luôn có VS.ABC <(abc√3)/6
Câu 2: Câu hỏi về hình lăng trụ
a) Cho hình lăng trụ ABCA’B’C’ có A’ABC là hình chóp tam giác đều, cạnh đáy AB = a, cạnh bên AA’ = b. Gọi α là góc giữa hai mặt phẳng (ABC) và (A’BC). Tính tanα và thể tích khối chópA’BB’C’C.
b)Trong mặt phẳng với hệ tọa độ Đề các vuông góc OXY tìm tọa độ các đỉnh của tam giác ABC cân tại A. Biết phương trình cạnh BC: x- y- 2= 0 .Đường phân giác trong của góc B có phương trình 2x- y- 9= 0 ,và đường cao qua điểm A của tam giác có phương trình x+ y- 4= 0.
Câu 3: Giải phương trình điều kiện tham số
Tìm tất cả các giá trị của tham số m, sao cho phương trình: x^3- 3mx^2+ 4= 0 có ba nghiệm phân biệt và
các nghiệm đều nhỏ hơn 4.
Câu 4: Bài toán đố về số nguyên
Cho số nguyên dương n. Gọi M là tập số tự nhiên (viết trong hệ thập phân) có n chữ số, các chữ số lớn hơn
1 và không có hai chữ số khác nhau cùng nhỏ hơn 7 đứng liền nhau.
1/ Chứng minh: trong M, số các số có tận cùng 2 bằng số các số có tân cùng 3.
2/ Tính số phần tử của M theo n.
Câu 5: Hình học không gian về quan hệ vuông góc
Cho tứ giác ABCD nội tiếp đường tròn và hai đường chéo vuông góc với nhau tại I; J là đỉnh thứ tư của hình
chữ nhật IBJC. Chứng minh: IJ vuông góc với AD
Câu 6: Hình học phẳng liên quan đến tam giác
Cho tam giác ABC có ba góc đều nhọn, H là trực tâm của tam giác đó. Gọi D là trung điểm của cạnh BC.
Các đường tròng đường kính BC và AD cắt nhau tại E và F. Chứng minh ba điểm E, H, F thẳng hàng.
Câu 7: Hình học phẳng liên quan đến đường tròn
Trong mặt phẳng cho hai đường tròn không bằng nhau ( O; R) và ( O’; R’), tiếp xúc ngoài với nhau tại A.
Điểm B di động trên đường tròn (O). Đường thẳng vuông góc với BA tại A cắt đường tròn (O’) tại C (khác A) .
1. Chứng minh rằng đường thẳng BC luôn luôn đi qua một điểm cố định.
2. Chứng minh rằng trọng tâm G của tam giác ABC luôn thuộc một đường tròn cố định, khi B thay đổi.
Câu 8: Bài toán đố
Cho n là một số nguyên dương. Gọi T là tập hợp tất cả các điểm (x, y) trong mặt phẳng, với x, y là các số
nguyên không âm, và x+y < n. Mỗi điểm của T được tô màu đỏ hoặc xanh. Nếu một điểm (x,y) là màu đỏ, thì mọi
điểm (x’, y’) của T cũng là màu đỏ, với x’ ≤ x và y’ ≤ y. Ta định nghĩa một kiểu tập hợp thứ nhất, gồm n điểm màu
xanh, có toạ độ x khác nhau, và một kiểu tập hợp thứ hai gồm n điểm màu xanh có toạ độ y khác nhau. Chứng
minh rằng số lượng hai kiểu tập hợp trên là bằng nhau.
Câu 9: Bài toán đố về hình học phẳng
Cho một hình lục giác lồi có tính chất sau: Với bất kỳ cặp cạnh đối diện nào, khoảng cách giữa hai trung
điểm của chúng đều bằng căn(3)/2 tổng độ dài hai cạnh đó. Chứng minh rằng tất cả các góc của lục giác đó bằng
nhau.
Đáp án đề thi
Bộ tài liệu cung cấp các đáp án chuẩn từ chính kì thi đề ra. Thuận lợi cho các bạn học sinh có thể tra cứu, tự làm lại nếu thấy thiếu sót.
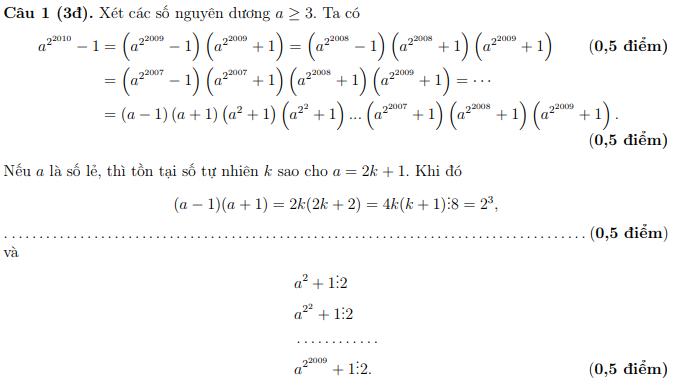


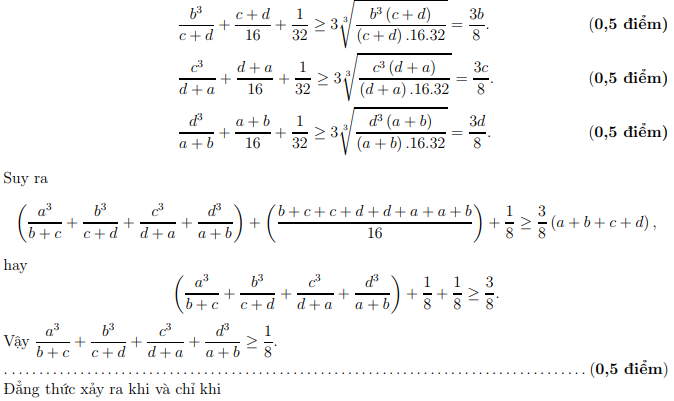
Trên đây là bộ đề thi hsg toán 12 mà chúng tôi đã gửi đến các bạn. Bộ đề thi học sinh giỏi toán học được chúng tôi sưu tầm và biên soạn một cách chọn lọc, cụ thể. Trong bộ tài liệu không chỉ có đề thi mà còn đi kèm với đáp án, các bạn có thể sử dụng để so sánh với kết quả của mình để biết mình sai ở đâu để mà rút kinh nghiệm cho các bài tập sau.




 056.3753648
056.3753648
 Chat FB
Chat FB