Tóm tắt tài liệu
Cách giải phương trình bậc 3 sẽ được đề cập chi tiết trong bài viết này. Như chúng ta đã biết, khác hoàn toàn với phương trình bậc nhất và phương trình bậc hai đã được giới thiệu từ trước. Thì phương trình bậc ba có khá nhiều điểm khác như số nghiệm và cả về độ đẹp của các nghiệm nữa. Tùy vào các hệ số mà ta có những phương pháp khác nhau.
Phương pháp tổng quát
Bất kể loại phương trình nào đều có phương pháp riêng để tiến hành giải. Hay còn gọi là những công thức tổng quát. Riêng phương trình bậc ba chúng ta sẽ tìm hiểu thông qua 3 hướng tiếp cận dựa vào mối liên hệ giữa các hệ số như sau:
Phương pháp phân tích thành nhân tử
Đây là phương pháp khá đơn giản tuy nhiên điều kiện của phương trình phải là có nghiệm đẹp. Nghiệm đẹp ở đây có thể là số nguyên hoặc là phân số. Sau khi tìm được nhân tử chung thứ nhất thì việc còn lại chỉ là giải một phương trình bậc hai vô cùng đơn giản
Khi một phương trình bậc 3 \[a{{x}^{3}}+b{{x}^{2}}+cx+d=0\] có nghiệm \[x=r\] thì chắc chắn nó sẽ xuất hiện nhân tử \[\left( xr \right)\]. Sau khi tìm được nghiệm chung, ta tiến hành phân tích thành nhân tử qua các bước sau:
Bước 1: Tìm nghiệm đơn giản của phương trình. Đối với các bài toán này thường có nghiệm khá đơn giản như 0,1,2,3. Nếu phức tạp hơn một tí thì có thể dùng máy tính casio để nhẩm nghiệm với chức năng solve.
Bước 2: Sau khi có nghiệm, ta tiến hành phép phân tích phân tử bằng cách chia tách các hệ số, sơ đồ hoocne hoặc phương pháp đồng nhất thức đều được cả.
Phương pháp Cardano
Phương pháp thiên về việc đặt ẩn phụ và khá phức tạp. Tuy nhiên lợi thế của phương pháp này là giải quyết hầu hết các bài tập phương trình bậc ba mà không cần quan tâm đến hệ số cũng như kết quả nghiệm xấu hay là đẹp. Đây là phương pháp giải được cho là tổng quát nhất và cũng khá là phức tạp:
Xét phương trình bậc 3: \[{{x}^{3}}+a{{x}^{2}}+bx+c=0\] (1)
Đặt \[x=y\frac{a}{3}\] thì phương trình (1) luôn biến đổi về dạng chính tắc là \[{{y}^{3}}+py+q=0\] trong đó:
- \[p=b\frac{{{a}^{2}}}{3}\]
- \[q=c+\frac{2{{a}^{3}}9ab}{27}\]
Trường hợp này ta chỉ xét \[p,q\ne 0\] còn trường hợp bằng 0 thì sẽ đưa về dạng đơn giản hơn rất nhiều.

Phương pháp lượng giác hóa
Một phương trình bậc ba, nếu có nghiệm thực, khi biểu diễn dưới dạng căn thức sẽ liên quan đến số phức. Vì vậy ta thường dùng phương pháp lượng giác hoá để tìm một cách biểu diễn khác đơn giản hơn, dựa trên hai hàm số cos và arcos.

Bài tập giải phương trình bậc 3 trong đề thi học sinh giỏi
Dưới đây là tổng hợp một số phương trình bậc 3 trong các đề thi học sinh giỏi đã diễn ra. Tuy các bài toán không xuất hiện ở dạng trực quan: “hãy giải phương trình bậc 3 sau?” mà chúng sẽ suất hiện dưới dạng một bài toán tổng hợp. Lồng ghép với các bài toán đại số khác để tạo thành một bài toán lớn.


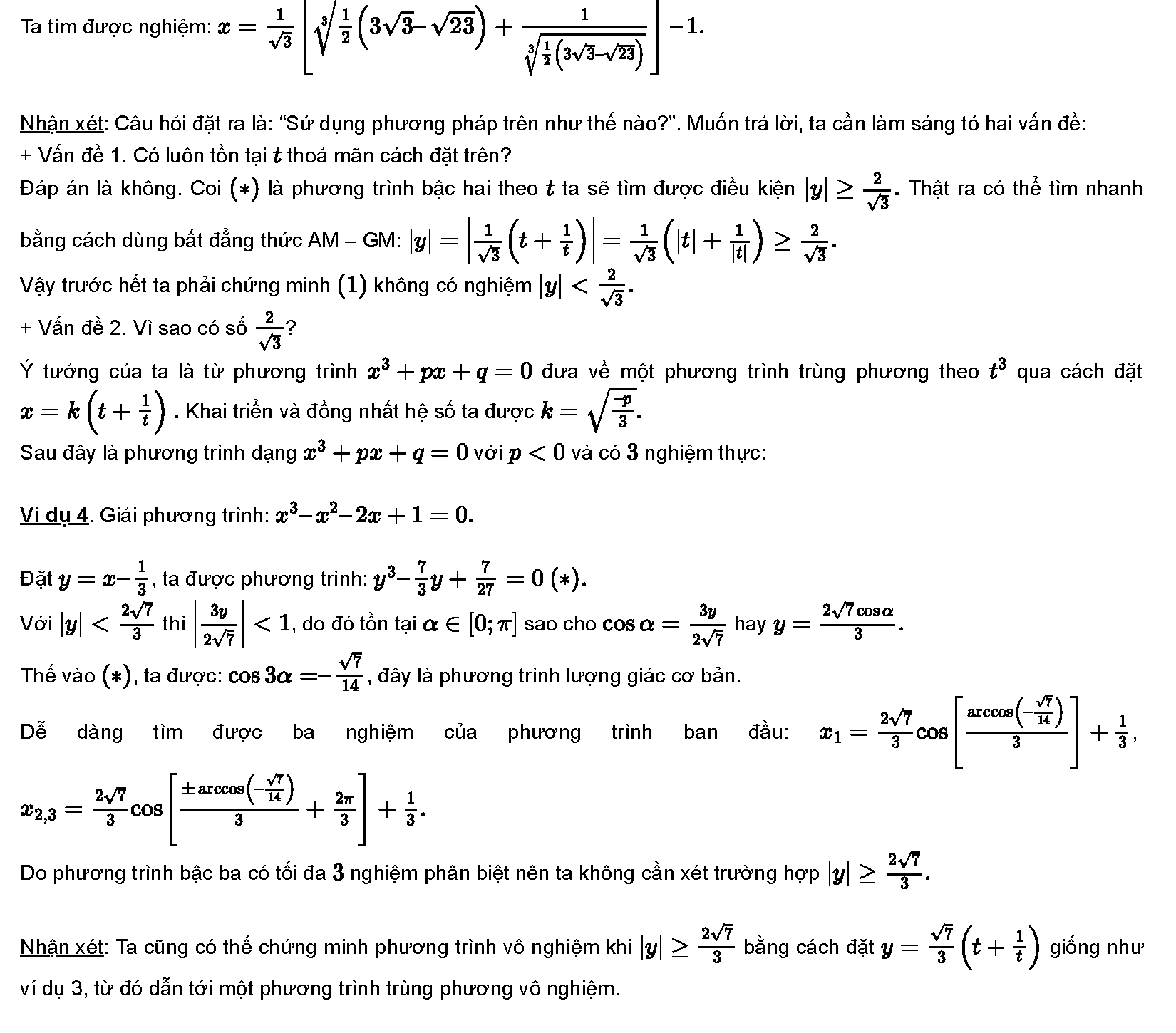

Vậy là chúng ta vừa tìm hiểu xong 3 cách giải phương trình bậc 3 cùng một số ví dụ rất hay về chuyên đề này. Để vận dụng một cách linh hoạt, các phương pháp thường kết hợp nhau hoặc loại trừ nhau. Có nhiều bài thích hợp dùng phương pháp này nhưng cũng có nhiều bài không thích hợp dùng. Do đó, chúng ta cần phải có hướng đi chính xác ngay khi gặp các phương trình bậc 3 trong đề thi. Cuối cùng thì chúc các em học tốt nhé.



 056.3753648
056.3753648
 Chat FB
Chat FB