Tài liệu gồm 98 trang tổng hợp chi tiết các chuyên đề bồi dưỡng học sinh giỏi hình học lớp 7. Ứng với các chuyên đề được phân thành các dạng bài tập chi tiết có lời giải. Các chuyên đề trong tài liệu bao gồm:
- Góc trong tam giác
- Các trường hợp bằng nhau của tam giác
- Các tam giác đặc biệt
- Bất đẳng thức trong tam giác
- Tính chất ba đường trung tuyến của tam giác


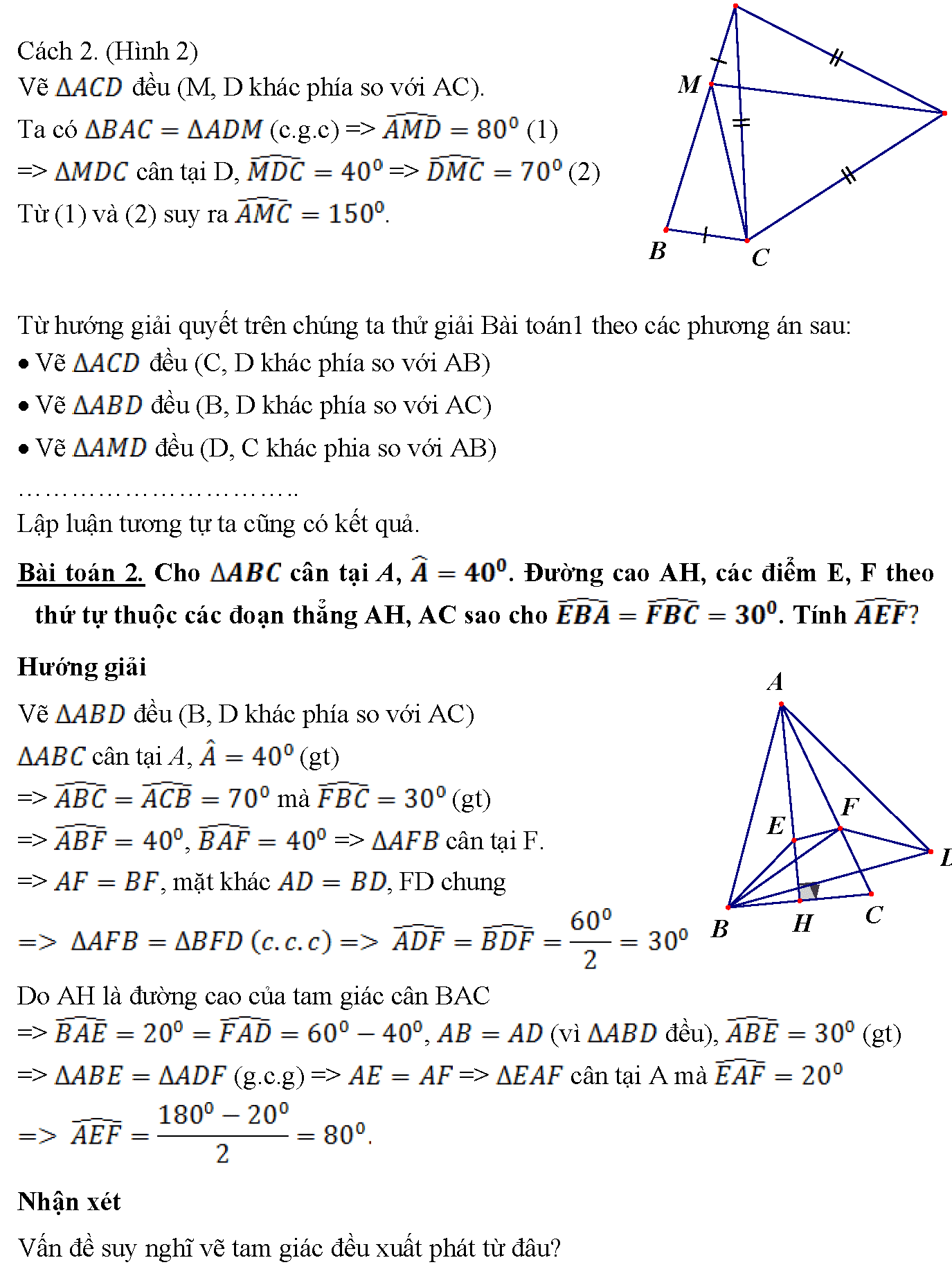








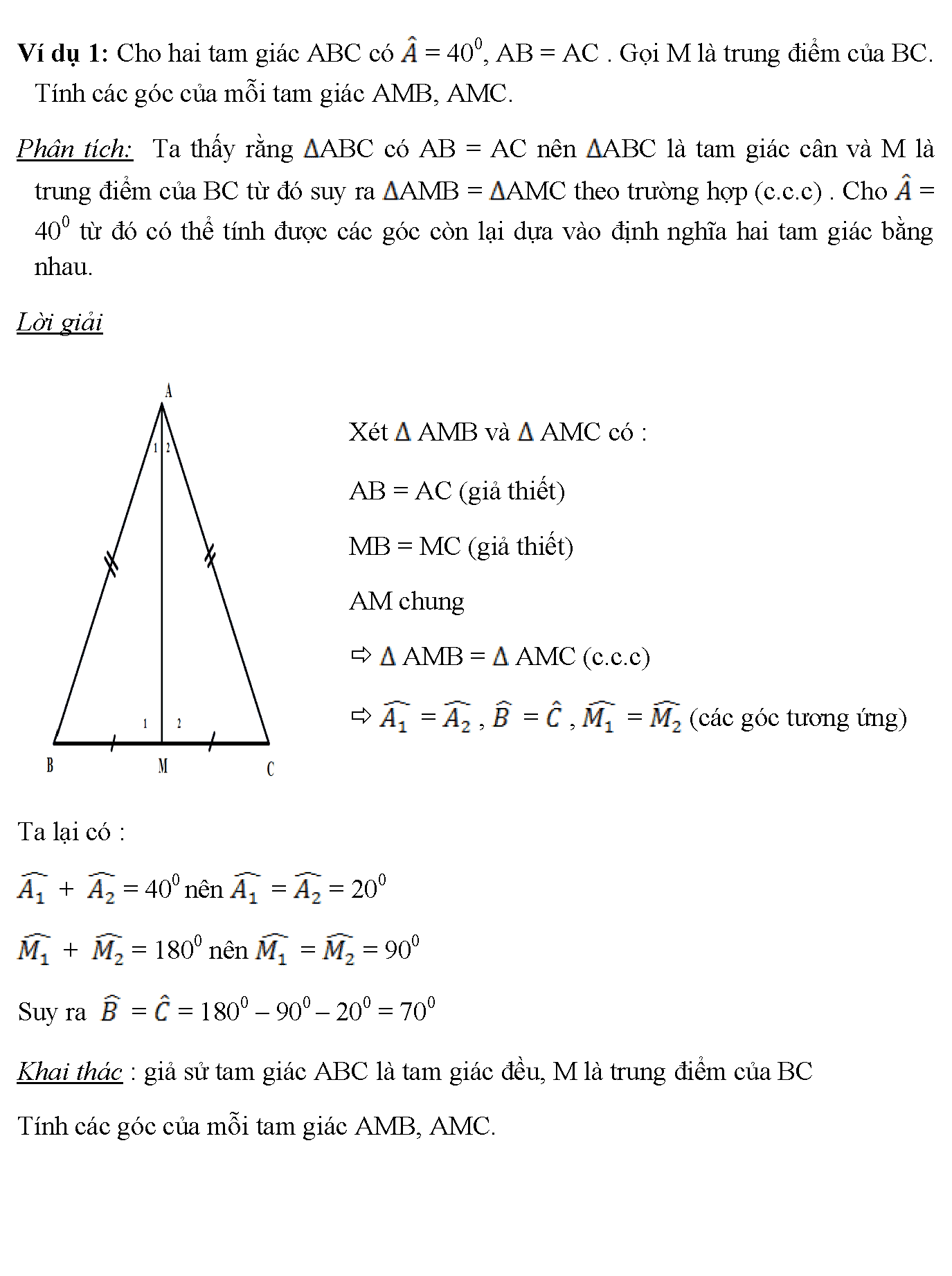
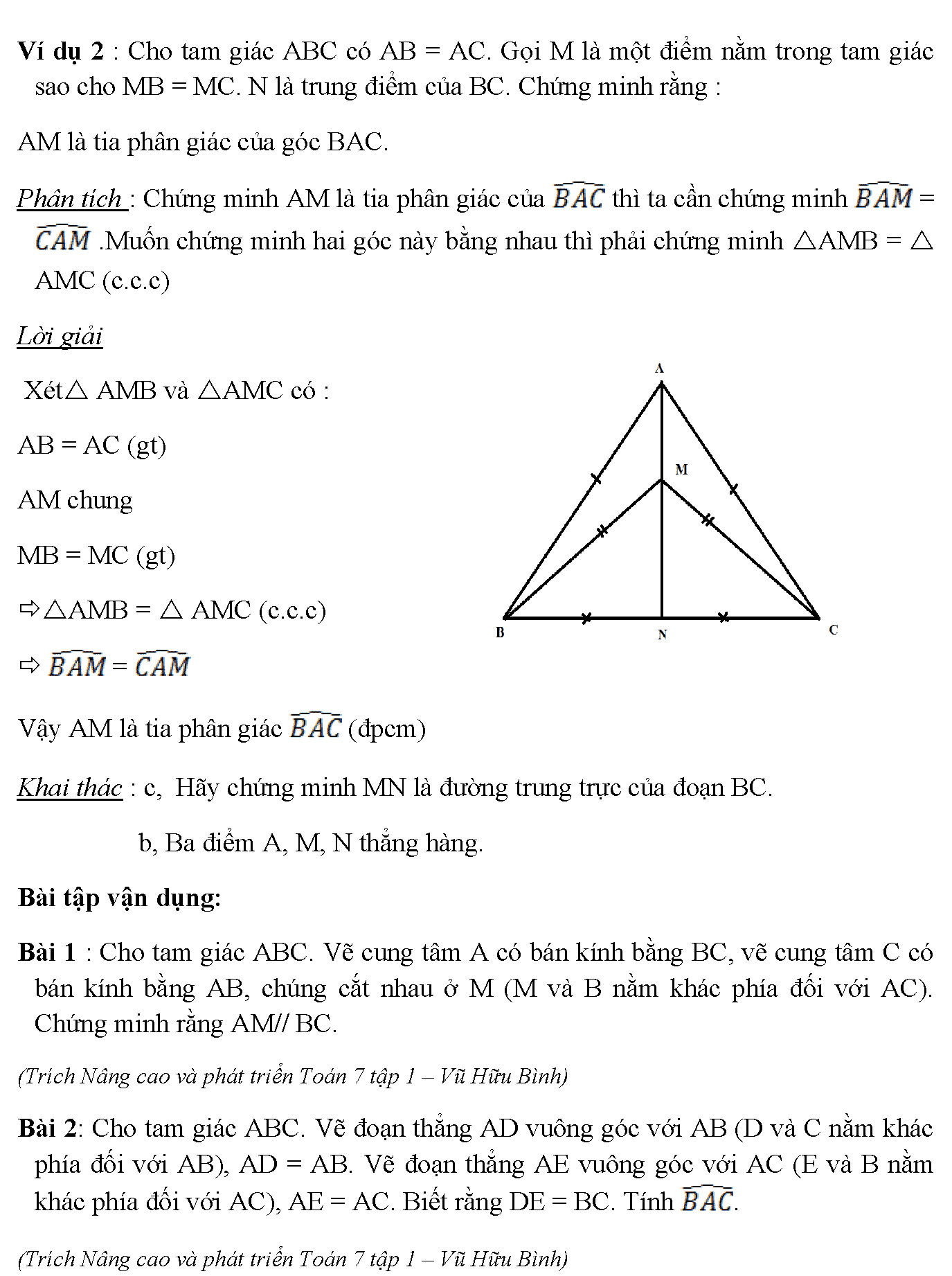
1. CÁC CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI HÌNH HỌC LỚP 7 CHUYÊN ĐỀ 1: GÓC TRONG TAM GIÁC I. Cơ sở lí thuyết Để giải tốt các bài toán tính số đo góc thì học sinh tối thiểu phải nắm vững các kiến thức sau: • Trong tam giác: o Tổng số đô ba góc trong tam giác bằng . o Biết hai góc ta xác địn được góc còn lại. o Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó. • Trong tam giác cân: biết một góc ta xác định được hai góc còn lại. • Trong tam giác vuông: o Biết một góc nhọn, xác định được góc còn lại. o Cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông có số đo bằng . • Trong tam giác vuông cân: mỗi góc nhọn có số đo bằng . • Trong tam giác đều: mỗi góc có số đo bằng . • Đường phân giác của một góc chia góc đó ra hai góc có số đo bằng nhau. • Hai đường phân giác của hai góc kề bù tạo thành một góc có số đo là . • Hai đường phân giác của hai góc kề phụ tạo thành một góc có số đo là . • Hai góc đối đỉnh thì bằng nhau. • Tính chất về góc so le trong, so le ngoài, đồng vị, hai góc trong cung phía, … Khi giải bài toán về tính số đo góc cần chú ý: 1. Vẽ hình chính xác, đúng với các số liệu trong đề bài để có hường chứng minh đúng. 2. Phát hiện các tam giác đều, “nửa tam giác đều”, tam giác vuông cân, tam giác cân trong hình vẽ. 3. Chú ý liên hệ giữa các góc của tam giác, liên hệ giữa các cạnh và các góc trong tam giác, phát hiện các cặp tam giác bằng nhau. Vẽ đường phụ hợp lí làm
2. xuất hiệ các góc đặc biệt, những cặp góc bằng nhau. Trong các đường phụ vẽ thêm, có thể vẽ đường phân giác, đường vuông góc, tam giác đều, … 4. Có thể dùng chữ để diễn đạt mối quan hệ giữa các góc. 5. Xét đủ các trường hợp về số đo góc có thể xảy ra (ví dụ góc nhọn, góc tù, …) (Tham khảo toán nâng cao lớp 7, tập 2 – Vũ Hữu Bình) Trong thực tế, để giải bài toán tính số đo góc ta thường xét các góc đó nằm trong mối liên hệ với các góc ở các hình đặc biệt đã nêu ở trên hoặc xét các góc tương ứng bằng nhau … rồi suy ra kết quả. Tuy nhiên, đứng trước một bài toán không phải lúc nào cũng gặp thuận lợi, có thể đưa về các trường hợp trên ngay mà có nhiều bài đòi hỏi người đọc phải tạo ra được những “điểm sáng bất ngờ” có thể là một đường kẻ phụ, một hình vẽ phụ… từ mối quan hệ giữa giả thiết, kết luận và những kiến thức, kỹ năng đã học trước đó mới giải quyết được. Chúng ta có thể xem “đường kẻ phụ”, “hình vẽ phụ” như là “chìa khoá “ thực thụ để giải quyết dạng toán này. II. Một số dạng toán và hướng giải quyết Dạng 1. Tính số đo góc qua việc phát hiện tam giác đều. Bài toán 1. Cho có có , lấy sao cho . Tính số đo Nhận xét Ta cần tìm thuộc có mà . Ta thấy có sự liên hệ rõ nét giữa góc và góc , mặt khác . Từ đây, ta thấy các yếu tố xuất hiệ ở trên liên quan đến tam giác đều. Điều này giúp ta nghĩ đến việc dựng hình phụ là tam giác đều. Hướng giải Cách 1. (Hình 1) Vẽ đều (D, A cùng phía so với BC). Nối A với D. Ta có (c.c.c) => Lại có (c.g.c) => =>
3. Cách 2. (Hình 2) Vẽ đều (M, D khác phía so với AC). Ta có (c.g.c) => (1) => cân tại D, => (2) Từ (1) và (2) suy ra . Từ hướng giải quyết trên chúng ta thử giải Bài toán1 theo các phương án sau: • Vẽ đều (C, D khác phía so với AB) • Vẽ đều (B, D khác phía so với AC) • Vẽ đều (D, C khác phia so với AB) ………………………….. Lập luận tương tự ta cũng có kết quả. Bài toán 2. Cho cân tại A, . Đường cao AH, các điểm E, F theo thứ tự thuộc các đoạn thẳng AH, AC sao cho . Tính Hướng giải Vẽ đều (B, D khác phía so với AC) cân tại A, (gt) => mà (gt) => , => cân tại F. => , mặt khác , FD chung Do AH là đường cao của tam giác cân BAC => , (vì đều), (gt) => (g.c.g) => => cân tại A mà Nhận xét Vấn đề suy nghĩ vẽ tam giác đều xuất phát từ đâu?
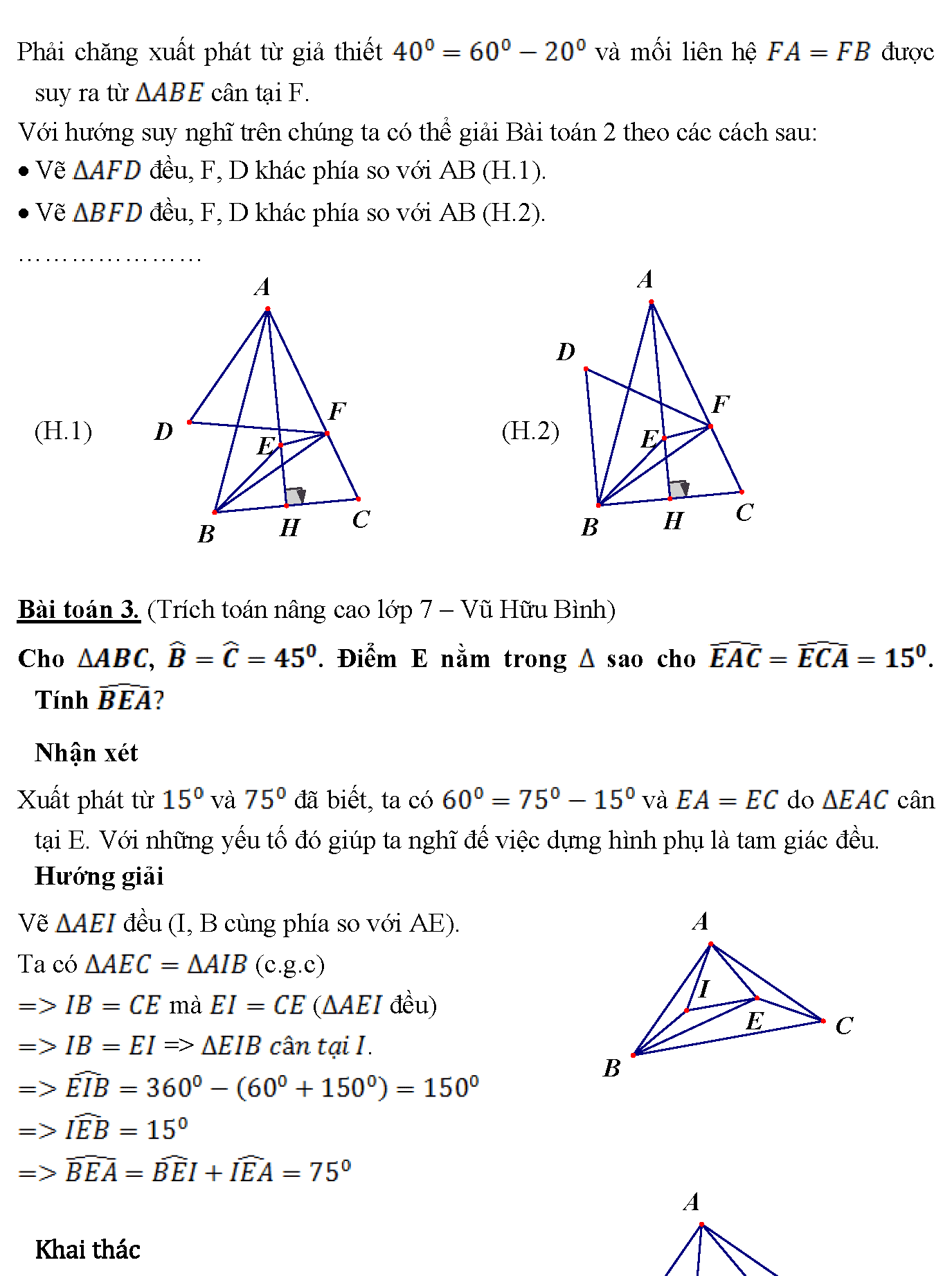
4. Phải chăng xuất phát từ giả thiết và mối liên hệ được suy ra từ cân tại F. Với hướng suy nghĩ trên chúng ta có thể giải Bài toán 2 theo các cách sau: • Vẽ đều, F, D khác phía so với AB (H.1). • Vẽ đều, F, D khác phía so với AB (H.2). ………………… (H.1) (H.2) Bài toán 3. (Trích toán nâng cao lớp 7 – Vũ Hữu Bình) Cho , . Điểm E nằm trong sao cho . Tính Nhận xét Xuất phát từ và đã biết, ta có và do cân tại E. Với những yếu tố đó giúp ta nghĩ đế việc dựng hình phụ là tam giác đều. Hướng giải Vẽ đều (I, B cùng phía so với AE). Ta có (c.g.c) mà ( đều) => . Khai thác
5. Chúng ta có thể giải Bài toán 3 theo cách sau: Vẽ đều (D, E khác phía so với AC) • Một số bài toán tương tự Bài toán 3.1. Cho , . Kẻ tia . Kẻ AD sao cho (B, D cùng phía so với AC). Tính Bài toán 3.2. Cho , (B, H khác phía so với AC). Tính Bài toán 3.3. Cho . Điểm M nằm trong tam giác sao cho . Tính Bài toán 4. Cho . M là điểm nằn trong tam giác sao cho . Tính Nhận xét Xuất phát từ giả thiết và liên hệ giữa góc với ta có . Từ đó nghĩ đến giải pháp dựng tam giác đều. Hướng giải Cách 1. (H.1) Vẽ đều (A, D cùng phía so với BC) Dễ thấy (c.g.c) và (g.c.g) cân tại B, Cách 2. (H.2) Vẽ (D, A khác phía so với BC)
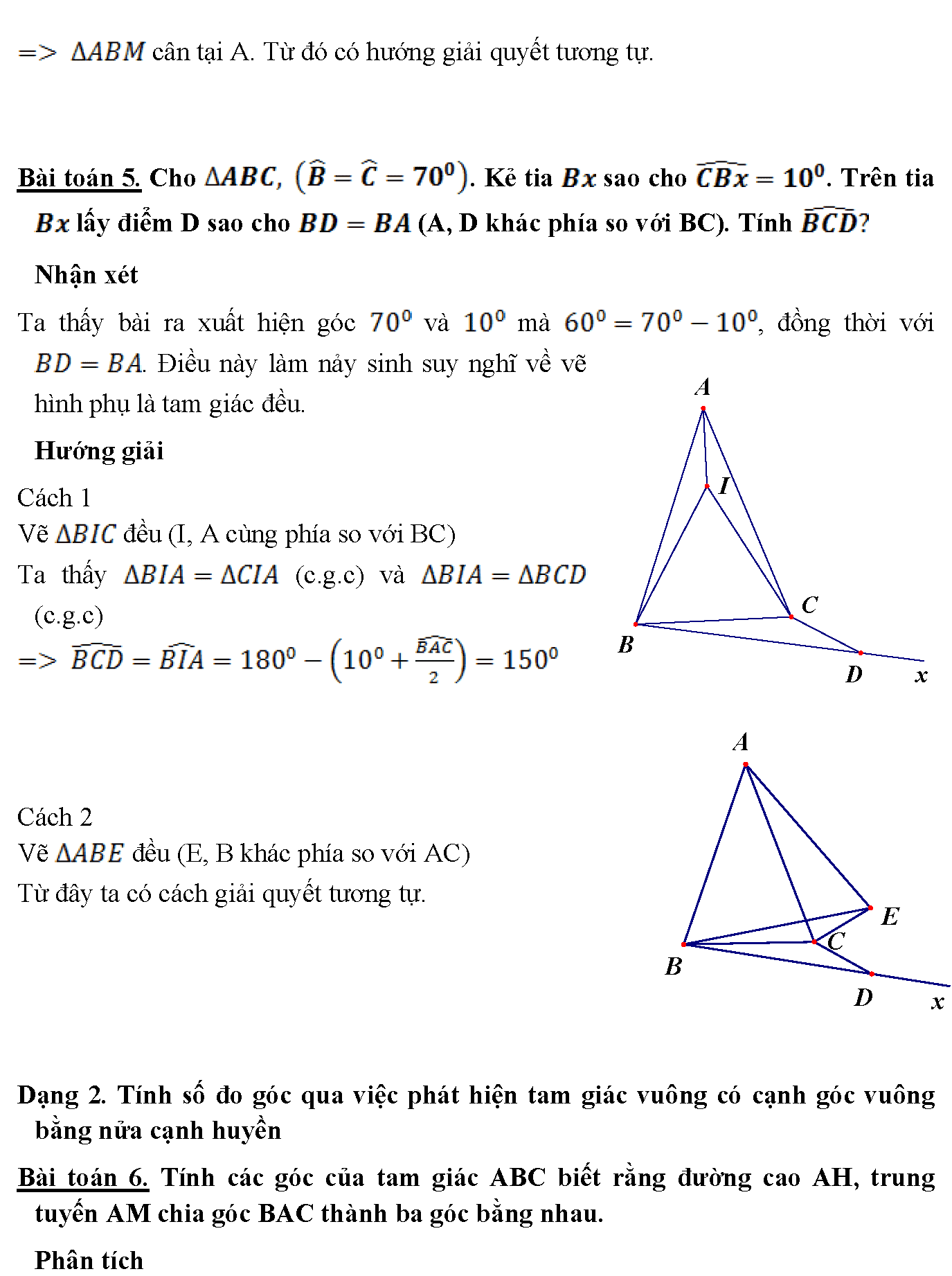
6. cân tại A. Từ đó có hướng giải quyết tương tự. Bài toán 5. Cho . Kẻ tia sao cho . Trên tia lấy điểm D sao cho (A, D khác phía so với BC). Tính Nhận xét Ta thấy bài ra xuất hiện góc và mà , đồng thời với . Điều này làm nảy sinh suy nghĩ về vẽ hình phụ là tam giác đều. Hướng giải Cách 1 Vẽ đều (I, A cùng phía so với BC) Ta thấy (c.g.c) và (c.g.c) Cách 2 Vẽ đều (E, B khác phía so với AC) Từ đây ta có cách giải quyết tương tự. Dạng 2. Tính số đo góc qua việc phát hiện tam giác vuông có cạnh góc vuông bằng nửa cạnh huyền Bài toán 6. Tính các góc của tam giác ABC biết rằng đường cao AH, trung tuyến AM chia góc BAC thành ba góc bằng nhau. Phân tích
7. +/ Đường cao AH, trung tuyến AM chia thành ba góc bằng nhau cân tại A (Đường cao đồng thời là phân giác) đồng thời là trung tuyến +/ Có thể vẽ thêm đường phụ liên quan đến và liên quan đến HM = HB = BM = MC Kẻ MK AC tại K. Khi đó có sơ sơ đồ phân tích. Hướng giải Vì tại K. Xét có AH là đường cao ứng với BM AH là đường phân giác ứng với cạnh BM (vì ) Nên cân tại đỉnh A => H là trung điểm BM Xét có AM là cạnh huyền chung (gt) (cạnh huyền – góc nhọn)
8. (hai cạnh tương ứng) Xét có , KM = MC khi đó ta tính được Vậy Bài toán 7. Cho . Đường cao AH AH = BC. D là trung điểm của AB. Tính Hướng giải cân tại C => CD là phân giác => Nhận xét Suy nghĩ chứng minh cân xuất phát từ đâu? Phải chăng xuất phát từ vuông có và AH = BC. Thực sự hai yếu tố này đã giúp ta nghĩ đến tam giác vuông có một góc bằng . Bài toán 8. Cho có ba góc nhọn. Về phía ngoài của ta vẽ các tam giác đều ABD và ACE. I là trực tâm , H là trung điểm BC. Tính Phân tích là một nửa tam giác đều =>, vẽ thêm đường phụ để xuất hiện nửa tam giác đều (còn lại) => Trên tia đối của tia HE lấy điểm F sao cho HE = HF Hướng giải Trên tia đối của tia HE lấy điểm F sao cho HE = HF
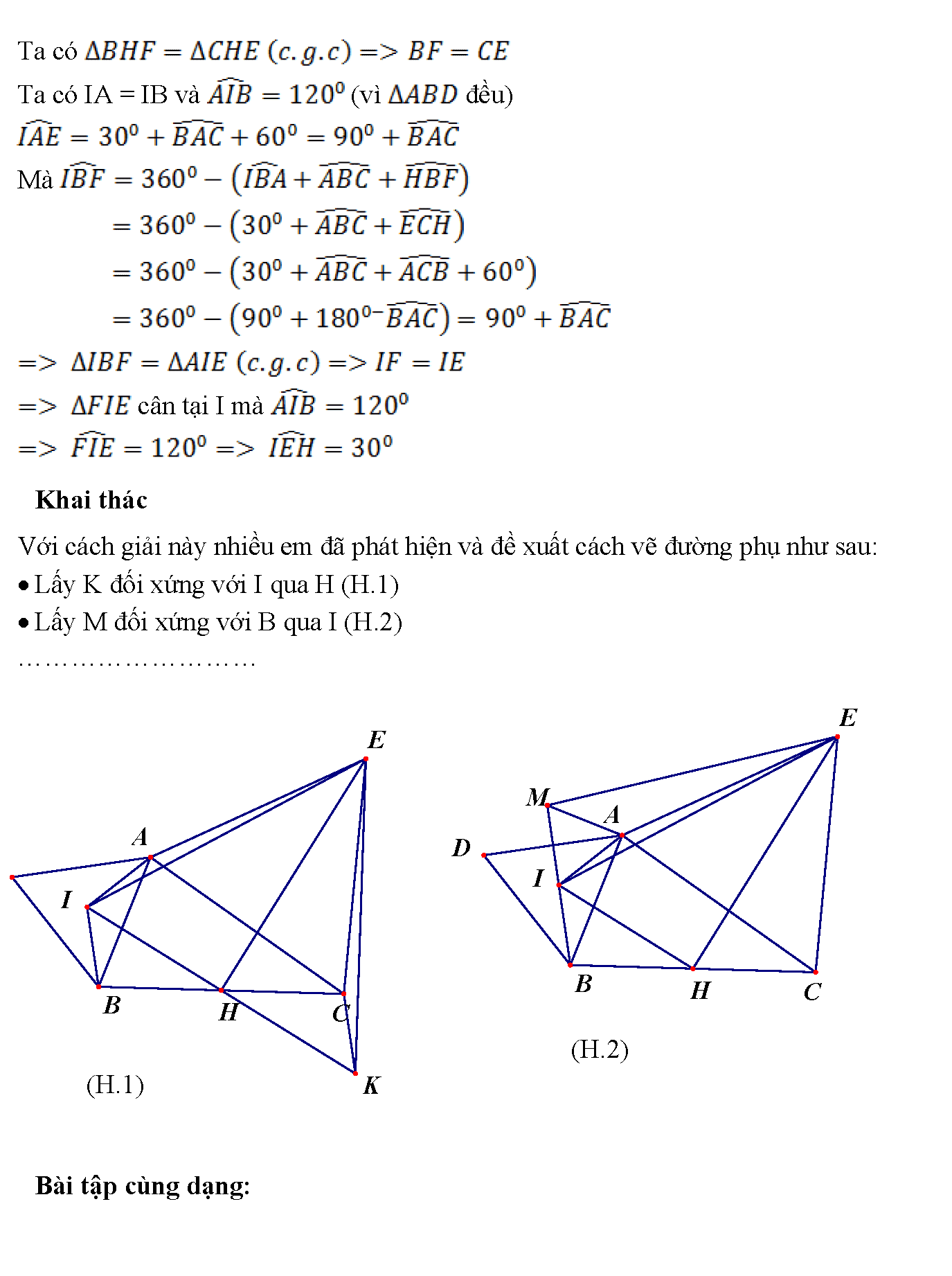
9. Ta có Ta có IA = IB và (vì đều) Mà cân tại I mà Khai thác Với cách giải này nhiều em đã phát hiện và đề xuất cách vẽ đường phụ như sau: • Lấy K đối xứng với I qua H (H.1) • Lấy M đối xứng với B qua I (H.2) ………………………
10. Cho , vẽ đều (E, D nằm ngoài tam giác). I, P lần lượt là trung điểm của AD và CE. Điểm F nằm trên BC sao cho BF = 3FC. Tính Dạng 3. Tính số đo góc qua việc phát hiện tam giác vuông cân Bài toán 9. Cho , M là trung điểm của BC, . Tính Phân tích Khi đọc kĩ bài toán ta thấy , quan sát hình vẽ rồi nhận dạng bài toán ta biết được nó có nguồn gốc từ Bài toán 3. Mặt khác , điều này giúp ta nghĩ đến dựng tam giác vuông cân. Hướng giải Cách 1. Hạ (Dễ chứng minh được tia CB nằm giữa hai tia CA và CK) Ta có vuông cân tại K (vì ) Vẽ vuông cân tại S (K, S khác phía so với AC) Do vuông tại K => KM = BC = MC cân tại M Dễ thấy và đều => AS = SM = AK cân tại A Cách 2. Lấy D đối xứng B qua AM => cân tại A
11. Ta có DC // MI (vì MB = MC, IB = ID), ( ) Mà Mặt khác xét có cân tại D => AD = CD Mà AD = BD ( đều) Vậy vuông cân tại D => Bài toán 10. Cho . D là điểm thuộc đoạn AC sao cho AD = 2DC. Tính Hướng giải Kẻ sao cho EA = ED, với EF = AD (B, F khác phía so với AC) Ta có (c.g.c) (*) vuông cân tại D (1) Trên tia đối của tia AB lấy I sao cho AI = 2AB Dễ thấy (c.g.c) => (2) Từ (*), (1) và (2) ta có Nhận xét Sau khi vẽ hình ta dự đoán lúc đó ta nghĩ đến việc tạo ra một tam giác vuông cân làm sao để tổng số đo của hai góc cần tìm bằng số đo góc . Ý nghĩ dự đoán xuất phát từ đâu? Phải chăng xuất phát từ vuông cân (E là trung điểm AD). Khi phát hiện tổng hai góc đó bằng chúng ta có thể giải bài toán theo nhiều cách giải khác nhau.
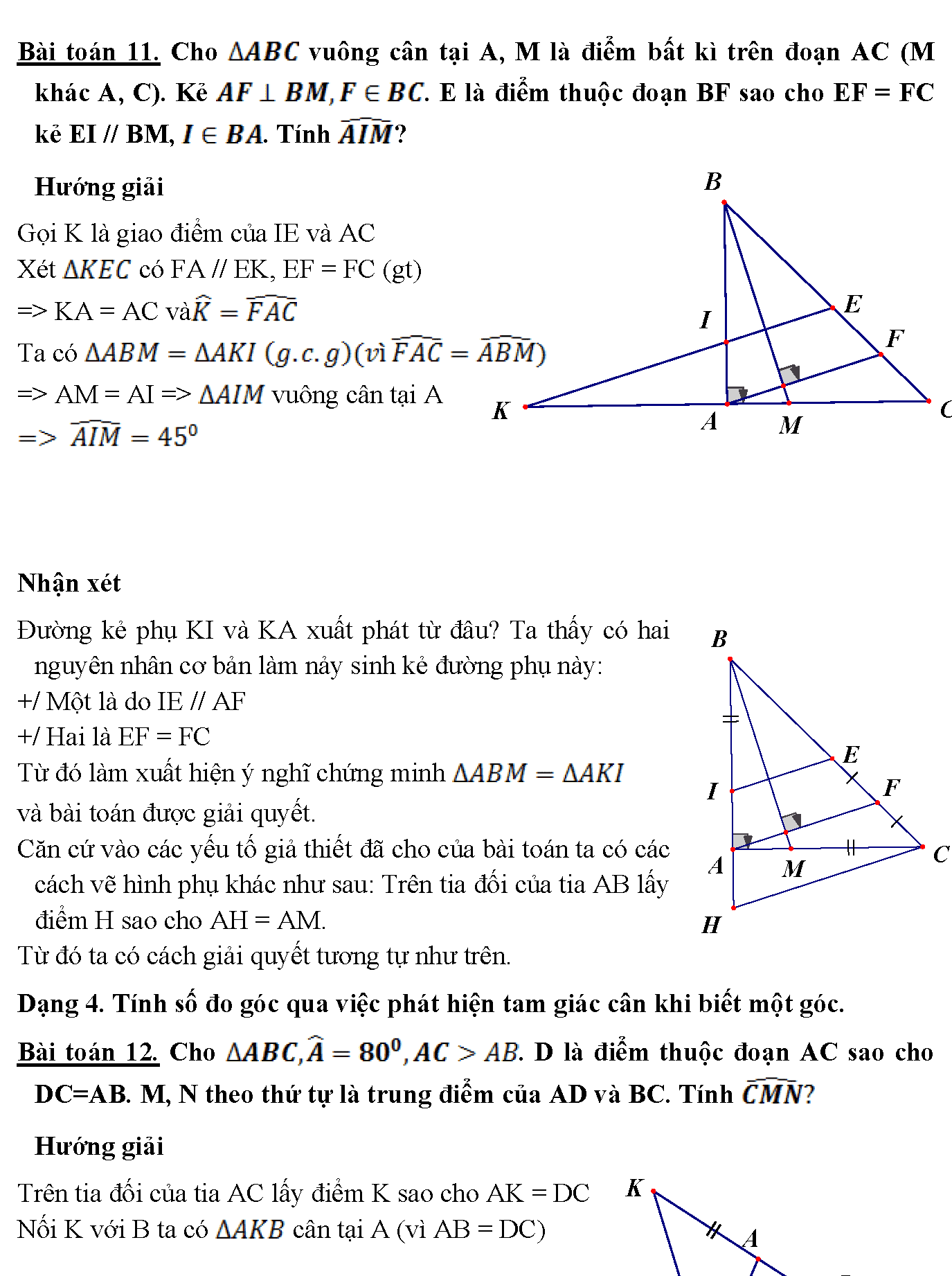
12. Bài toán 11. Cho vuông cân tại A, M là điểm bất kì trên đoạn AC (M khác A, C). Kẻ . E là điểm thuộc đoạn BF sao cho EF = FC kẻ EI // BM, . Tính ? Hướng giải Gọi K là giao điểm của IE và AC Xét có FA // EK, EF = FC (gt) => KA = AC và Ta có => AM = AI => vuông cân tại A Nhận xét Đường kẻ phụ KI và KA xuất phát từ đâu? Ta thấy có hai nguyên nhân cơ bản làm nảy sinh kẻ đường phụ này: +/ Một là do IE // AF +/ Hai là EF = FC Từ đó làm xuất hiện ý nghĩ chứng minh và bài toán được giải quyết. Căn cứ vào các yếu tố giả thiết đã cho của bài toán ta có các cách vẽ hình phụ khác như sau: Trên tia đối của tia AB lấy điểm H sao cho AH = AM. Từ đó ta có cách giải quyết tương tự như trên. Dạng 4. Tính số đo góc qua việc phát hiện tam giác cân khi biết một góc. Bài toán 12. Cho . D là điểm thuộc đoạn AC sao cho DC=AB. M, N theo thứ tự là trung điểm của AD và BC. Tính Hướng giải Trên tia đối của tia AC lấy điểm K sao cho AK = DC Nối K với B ta có cân tại A (vì AB = DC)
13. Mặt khác ta có MA = MD => MK = MC, BN = NC => MN là đường trung bình của Nhận xét Vì đâu ta có kẻ đường phụ AK? +/ Thứ nhất: Ta có cân và biết . Như vậy các góc của sẽ tìm được. +/ Thứ hai: Vì MA = MD dẫn đến MK = MC +/ Thứ ba: Do NB = MC Với lí do thứ hai và ba ta có được góc cần tìm bằng . Vậy bài toán được giải quyết. Sau khi nêu ra các lí do cơ bản đó, ta có các đường kẻ phụ khác như sau: • Lấy K đối xứng với A qua N • Lấy K là trung điểm của BD • Lấy K đối xứng M qua B • Lấy K đối xứng D qua N ………………………… Bài toán trên có thể ra dưới dạng tổng quát như sau: Giữ nguyên giả thiết và thay Một số bài toán tham khảo Bài 1. Cho , các phân giác AD, CE cắt nhau tại F, , . Tính Bài 2. Cho , CA = CB, điểm M nằm trong tam giác sao cho . Tính Bài 3. Cho cân tại C, , M nằm trong tam giác sao cho . Tính Bài 4. Cho AB = AC, , trung tuyến CM. trên tia đối của tia BA lấy điểm D sao cho BD = BA, biết . Tính
14. CHUYÊN ĐỀ 2 : CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC A, Tóm tắt lý thuyết 1.Hai tam giác bằng nhau: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau. ABC = A’B’C’ 2. Các trường hợp bằng nhau của tam giác a.Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh ( c.c.c )
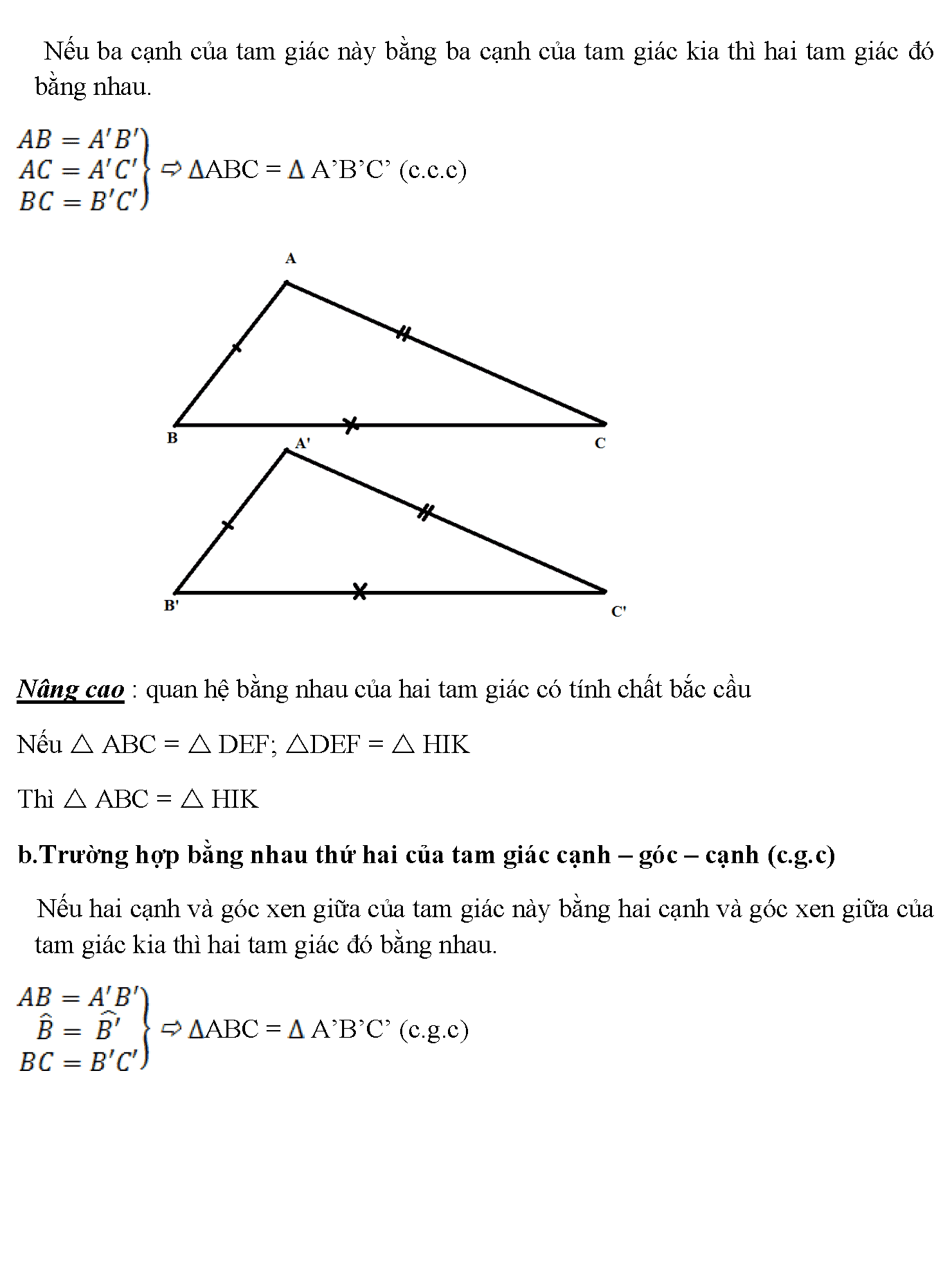
15. Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. ABC = A’B’C’ (c.c.c) Nâng cao : quan hệ bằng nhau của hai tam giác có tính chất bắc cầu Nếu ABC = DEF; DEF = HIK Thì ABC = HIK b.Trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh (c.g.c) Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. ABC = A’B’C’ (c.g.c)
16. Hệ quả : Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Nâng cao : Trong trường hợp bằng nhau cạnh – góc – cạnh, cặp góc bằng nhau phải là cặp góc xen giữa hai cặp cạnh bằng nhau. Nếu không có điều kiện đó thì hai tam giác chưa chắc đã bằng nhau. Tuy nhiên, người ta đã chứng minh được rằng : Nếu hai tam giác nhọn có hai cặp cạnh bằng nhau từng đôi một và một cặp góc tương ứng bằng nhau (không cần xen giữa) thì hai tam giác đó bằng nhau. c.Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc ( g.c.g ) Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau. ABC = A’B’C’ ( g.c.g )
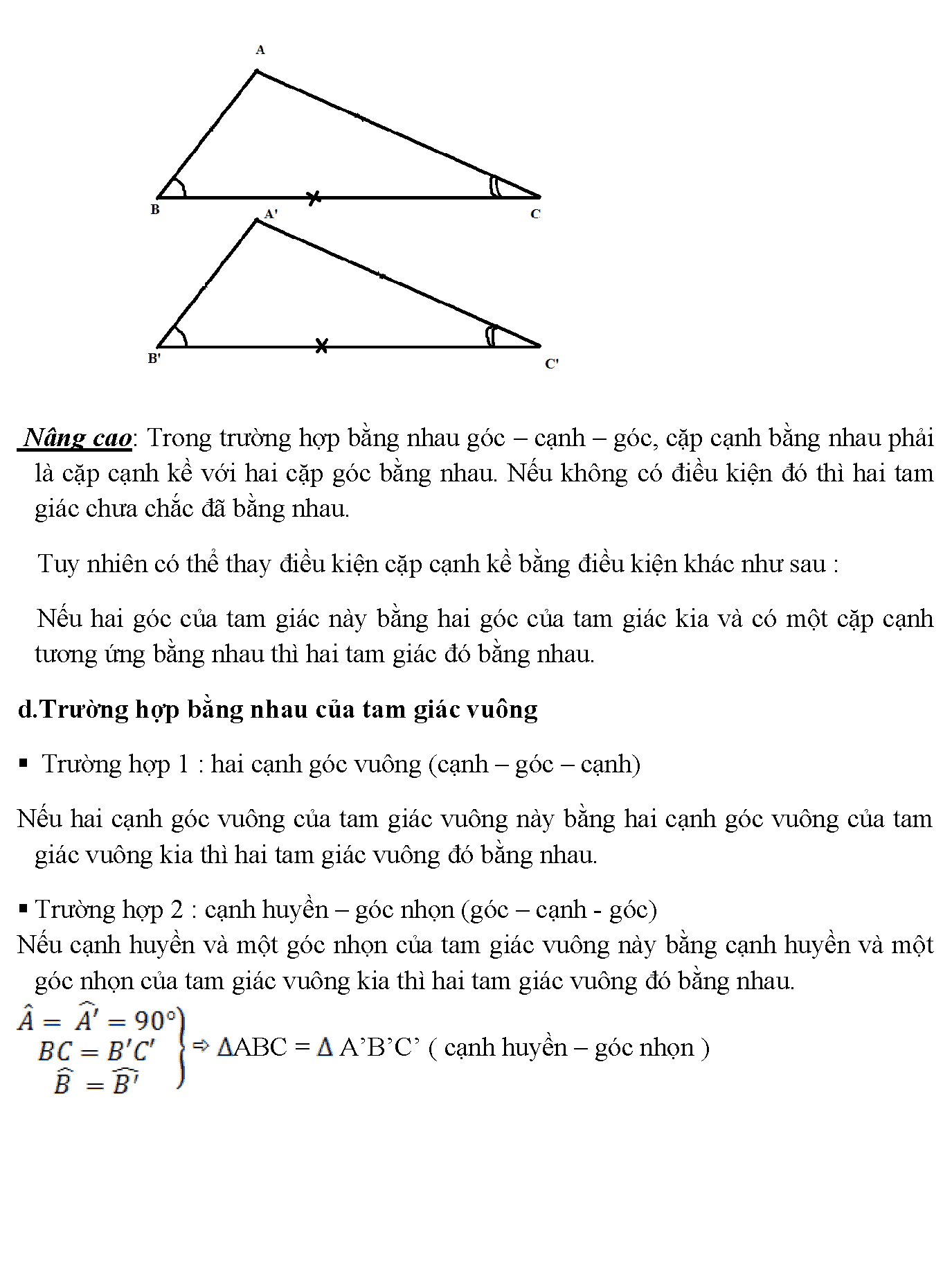
17. Nâng cao: Trong trường hợp bằng nhau góc – cạnh – góc, cặp cạnh bằng nhau phải là cặp cạnh kề với hai cặp góc bằng nhau. Nếu không có điều kiện đó thì hai tam giác chưa chắc đã bằng nhau. Tuy nhiên có thể thay điều kiện cặp cạnh kề bằng điều kiện khác như sau : Nếu hai góc của tam giác này bằng hai góc của tam giác kia và có một cặp cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau. d.Trường hợp bằng nhau của tam giác vuông Trường hợp 1 : hai cạnh góc vuông (cạnh – góc – cạnh) Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Trường hợp 2 : cạnh huyền – góc nhọn (góc – cạnh – góc) Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ABC = A’B’C’ ( cạnh huyền – góc nhọn )
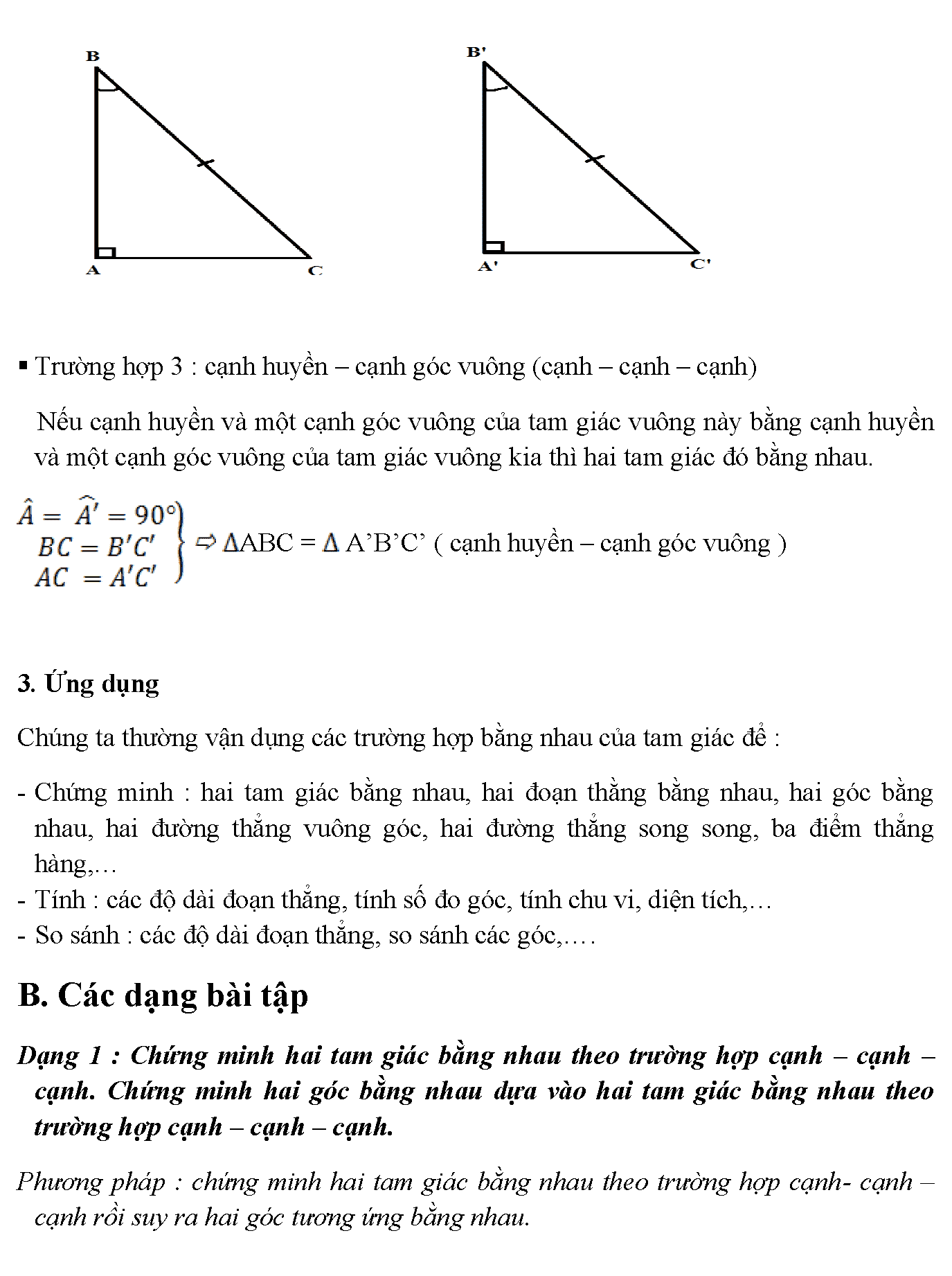
18. Trường hợp 3 : cạnh huyền – cạnh góc vuông (cạnh – cạnh – cạnh) Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau. ABC = A’B’C’ ( cạnh huyền – cạnh góc vuông ) 3. Ứng dụng Chúng ta thường vận dụng các trường hợp bằng nhau của tam giác để : – Chứng minh : hai tam giác bằng nhau, hai đoạn thằng bằng nhau, hai góc bằng nhau, hai đường thẳng vuông góc, hai đường thẳng song song, ba điểm thẳng hàng,… – Tính : các độ dài đoạn thẳng, tính số đo góc, tính chu vi, diện tích,… – So sánh : các độ dài đoạn thẳng, so sánh các góc,…. B. Các dạng bài tập Dạng 1 : Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh. Chứng minh hai góc bằng nhau dựa vào hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh. Phương pháp : chứng minh hai tam giác bằng nhau theo trường hợp cạnh- cạnh – cạnh rồi suy ra hai góc tương ứng bằng nhau.
19. Ví dụ 1: Cho hai tam giác ABC có = 400, AB = AC . Gọi M là trung điểm của BC. Tính các góc của mỗi tam giác AMB, AMC. Phân tích: Ta thấy rằng ABC có AB = AC nên ABC là tam giác cân và M là trung điểm của BC từ đó suy ra AMB = AMC theo trường hợp (c.c.c) . Cho = 400 từ đó có thể tính được các góc còn lại dựa vào định nghĩa hai tam giác bằng nhau. Lời giải Xét AMB và AMC có : AB = AC (giả thiết) MB = MC (giả thiết) AM chung AMB = AMC (c.c.c) = , = , = (các góc tương ứng) Ta lại có : + = 400 nên = = 200 + = 1800 nên = = 900 Suy ra = = 1800 – 900 – 200 = 700 Khai thác : giả sử tam giác ABC là tam giác đều, M là trung điểm của BC Tính các góc của mỗi tam giác AMB, AMC.
20. Ví dụ 2 : Cho tam giác ABC có AB = AC. Gọi M là một điểm nằm trong tam giác sao cho MB = MC. N là trung điểm của BC. Chứng minh rằng : AM là tia phân giác của góc BAC. Phân tích : Chứng minh AM là tia phân giác của thì ta cần chứng minh = .Muốn chứng minh hai góc này bằng nhau thì phải chứng minh AMB = AMC (c.c.c) Lời giải Xét AMB và AMC có : AB = AC (gt) AM chung MB = MC (gt) AMB = AMC (c.c.c) = Vậy AM là tia phân giác (đpcm) Khai thác : c, Hãy chứng minh MN là đường trung trực của đoạn BC. b, Ba điểm A, M, N thẳng hàng. Bài tập vận dụng: Bài 1 : Cho tam giác ABC. Vẽ cung tâm A có bán kính bằng BC, vẽ cung tâm C có bán kính bằng AB, chúng cắt nhau ở M (M và B nằm khác phía đối với AC). Chứng minh rằng AM// BC. (Trích Nâng cao và phát triển Toán 7 tập 1 – Vũ Hữu Bình) Bài 2: Cho tam giác ABC. Vẽ đoạn thẳng AD vuông góc với AB (D và C nằm khác phía đối với AB), AD = AB. Vẽ đoạn thẳng AE vuông góc với AC (E và B nằm khác phía đối với AC), AE = AC. Biết rằng DE = BC. Tính . (Trích Nâng cao và phát triển Toán 7 tập 1 – Vũ Hữu Bình)




 056.3753648
056.3753648
 Chat FB
Chat FB