Tóm tắt tài liệu
Hàm số lũy thừa, hàm số mũ và hàm số logarit là các dạng hàm số mà các em học sinh được tiếp xúc lần đầu trong chương 2 đại số lớp 12. Đây là một chương có khá nhiều kiến thức cũng như công thức mà các em phải nắm chắc để làm bài tập. Cũng như giải quyết khá nhiều bài tập trắc nghiệm dễ đánh lừa. Dưới đây là tài liệu rất hay được chúng tôi biên soạn và tổng hợp lại với nội dung khá đầy đủ. Các vấn đề lý thuyết, phân dạng bài tập và cả những câu trắc nghiệm có lời giải chi tiết đều được trình bày một cách chi tiết nhất.

1. Lũy thừa
Ở phần lý thuyết này, chúng ta cùng tìm hiểu một số công thức cũng như các điểm lý thuyết dưới đây:
- Lũy thừa số mũ nguyên dương
- Lũy thừa số mũ 0 – Lũy thừa số mũ nguyên âm
- Lũy thừa số mũ hữu tỷ
- Lũy thừa số thực
- Tính chất của lũy thừa số mũ nguyên
- Định nghĩa công thức lãi kép
- Công thức lãi kép cần phải ghi nhớ
2. Logarit
- Định nghĩa và ý nghĩa của logarit
- Tính chất logarit
- Các quy tắc tính logarit
- Đổi cơ số logarit
- Logarit thập phân, logarit tự nhiên
2. Hàm số lũy thừa
- Một số vấn đề luyết quan trọng được nhắc đến như:
- Định nghĩa hàm số lũy thừa
- Tập xác định
- Đạo hàm của hàm số
- Tính chất của hàm số
3. Hàm số logarit
- Định nghĩa hàm số logarit
- Đạo hàm của hàm số logarit
- Khảo sát hàm số logarit: Chiều biến thiên, Tiệm cận, đồ thị, tập xác định của hàm số
4. Hàm số mũ
- Định nghĩa
- Đạo hàm
- Khảo sát hàm số: Tập xác định, Tiệm cận, Đồ thị hàm số
5. Câu hỏi trắc nghiệm hàm số lũy thừa
Câu 1. Cho các mệnh đề sau:
(I). Cơ số của logarit phải là số nguyên dương.
(II). Chỉ số thực dương mới có logarit. Mệnh đề nào đúng ??
Câu 2. Cho a, A, B, M, N là các số thực với a, M, N dương và khác 1. Có bao nhiêu phát biểu đúng trong các phát biểu dưới đây?
Câu 3. Tính giá trị của biểu thức logarit sau
Câu 4. Tính tổng T tất cả các nghiệm của phương trình
Câu 5. Biết rằng phương trình có nghiệm duy nhất. Khẳng định nào sau đây đúng?
Câu 9. Tìm tập S nghiệm của phương trình mũ sau:
Câu 12. Tính P là tổng bình phương tất cả các nghiệm
Câu 13. Gọi S là tập nghiệm của phương trình
Câu 14. Phương trình sau có tất cả bao nhiêu nghiệm
6. Bài tập trắc nghiệm hàm số mũ và logarit
Cùng tìm hiểu một số bài tập trắc nghiệm hàm số mũ và logarit sau. Các bài tập đều có lời giải chi tiết và phân dạng, định hướng rõ ràng. Đây là một tài liệu cực hay về chuyên đề này khi nó có cả ví dụ, bài tập mẫu. Các em hãy cùng theo dõi dưới đây nhé:





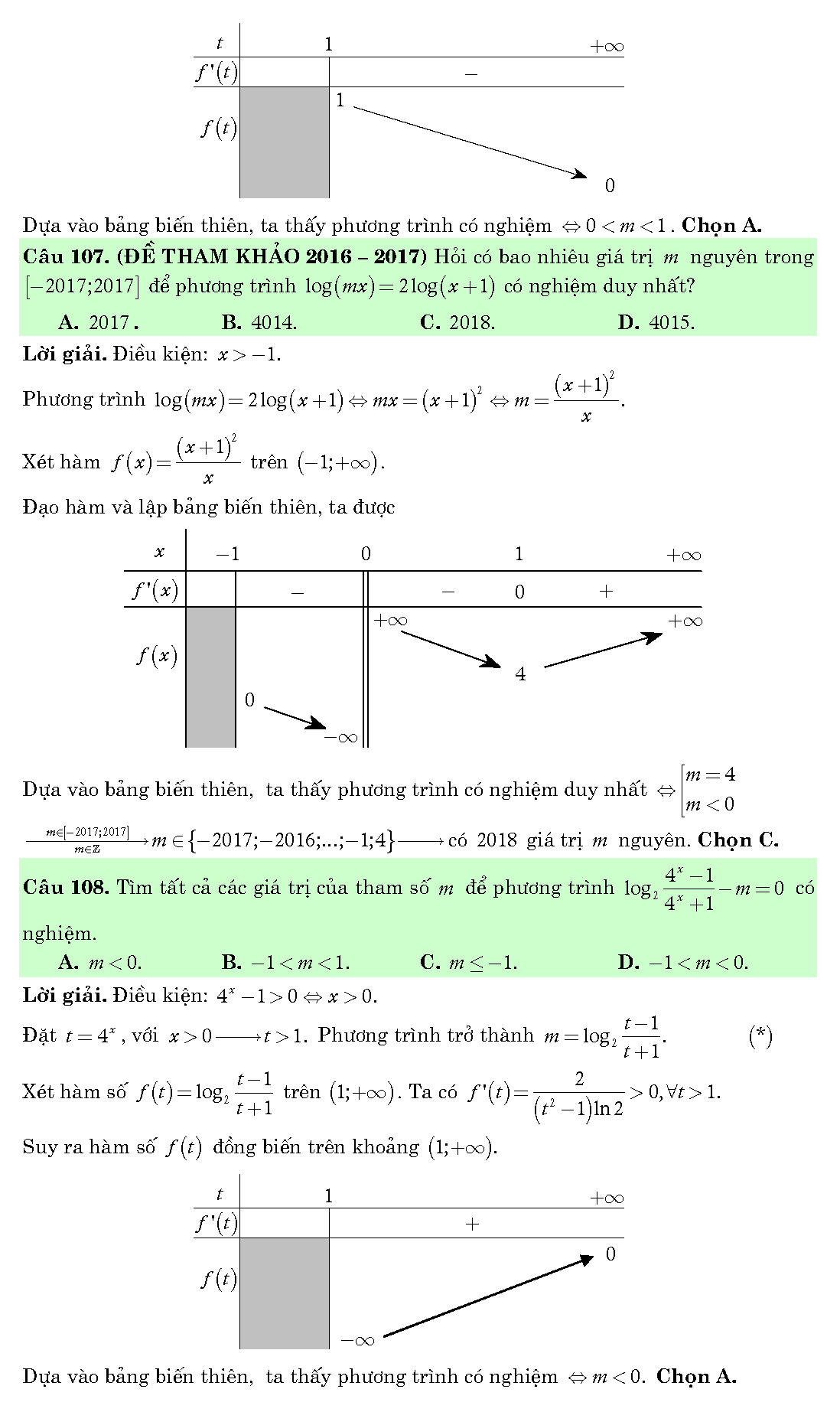

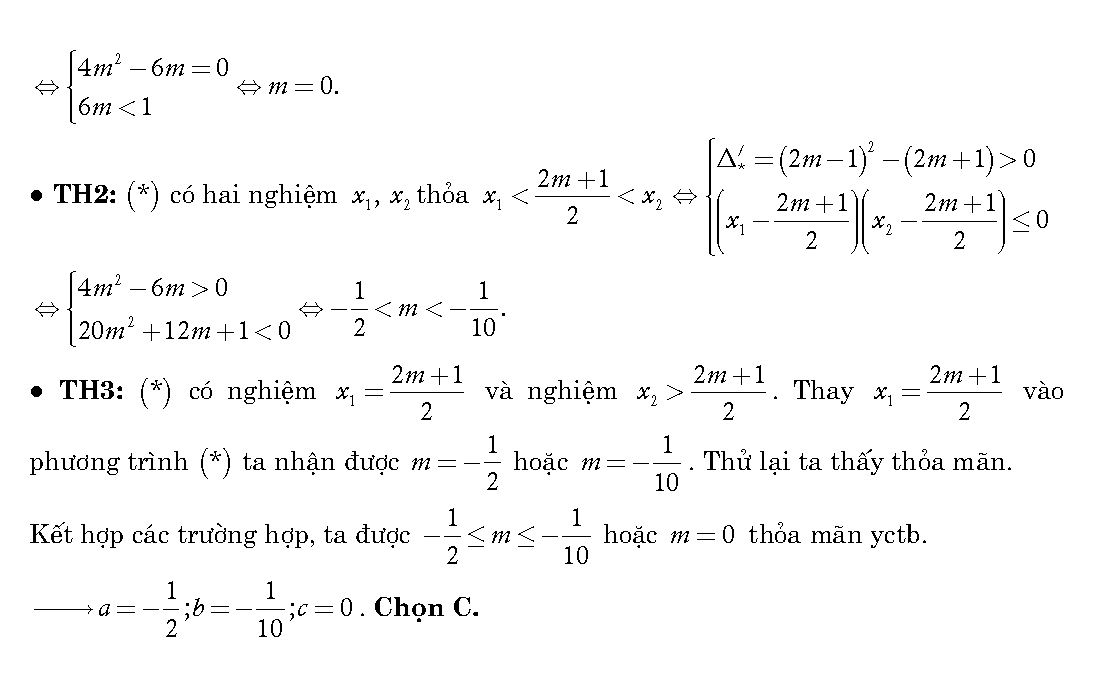



Vậy là chúng ta vừa tìm hiểu xong khá nhiều bài tập về hàm số lũy thừa, hàm số mũ và hàm số logarit trong tài liệu. Đây là một chương không quá khó, tuy nhiên để học tốt chương này thì các em cần phải học thuộc khá nhiều công thức và cách ứng dụng các công thức đó. Ngoài ra, việc vận dụng linh hoạt các công thức còn giúp các em rất nhiều trong việc tăng tốc tối đa khi làm trắc nghiệm. Chúc các em học tốt!




 056.3753648
056.3753648
 Chat FB
Chat FB