Tóm tắt tài liệu
Quan hệ vuông góc trong không gian là một chuyên đề hình học không gian rất quan trọng. Những bài toán về quan hệ vuông góc cũng như song song là nền tảng để hình học không gian phát triển theo nhiều hướng khác nhau. Ở tài liệu này, quan hệ vuông góc sẽ được trình bày một cách rõ ràng, chi tiết về cả vấn đề lý thuyết cũng như bài tập. Đây là một đề tài nghiên cứu, tuy nhiên lượng kiến thức được sắp xếp khá logic. Đề tài được bình chọn hay nhất bởi một số trường THPT về chuyên đề hình học.
Một số vấn đề được trình bày trong tài liệu được tóm tắt xuống phía dưới đây:
1. ĐỊNH NGHĨA – LÝ THUYẾT QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
1.1. Các định nghĩa
- Hai đường thẳng vuông góc
- Đường thẳng vuông góc với mặt phẳng
- Hai mặt phẳng vuông góc
- Góc giữa hai đường thẳng
- Góc giữa hai mặt phẳng
- Công thức khoảng cách từ một điểm đến một mặt phẳng
- Khoảng cách một đường thẳng đến một mặt phẳng
- Khoảng cách giữa hai mặt phẳng song song
- Khoảng cách giữa hai đường thẳng chéo nhau
1.2. Các định lí thường sử dụng
Trong tài liệu có tất cả 6 định lí mà chúng ta thường gặp nhất trong các bài toán quan hệ vuông góc. Để làm tốt thì các em cần phải nắm vững các định lí đó, áp dụng một cách nhanh chóng vào từng trường hợp.
2. CÁC DẠNG TOÁN VỀ CHỨNG MINH QUAN HỆ VUÔNG GÓC
2.1. Dạng 1: Chứng minh đường thẳng vuông góc với mặt phẳng
2.2. Dạng 2: Chứng minh hai đường thẳng vuông góc
2.3. Dạng 3: Chứng minh hai mặt phẳng vuông góc
3. CÁC DẠNG TOÁN VỀ GÓC
3.1. Dạng 1: Góc giữa hai đường thẳng
Ta thường vận dụng định lý 1 để chứng minh. Hoặc sử dụng định lý 3, định lý 5, định lý 6 trong một số trường hợp đặc biệt
3.2. Dạng 2: Góc giữa đường thẳng và mặt phẳng
Ta thường sử dụng định lý 2 hoặc là các cách chứng minh vuông góc có trong hình học phẳng
3.3. Dạng 3: Góc giữa hai mặt phẳng
Sử dụng định lý 3
4. CÁC DẠNG TOÁN VỀ KHOẢNG CÁCH
4.1. Dạng 1: Khoảng cách từ một điểm tới một mặt phẳng
Cách 1: (a,b)=(a’,b’) trong đó a’, b’ là hai đường thẳng cắt nhau và lần lượt song song với a và b. Tức là, chọn ra hai đường thẳng cắt nhau và lần lượt song song với a và b
Cách 2: (a,b)=(a,b’) trong đó b’ là đường thẳng cắt đường thẳng a và song song với b. Tức là chọn trên a (hoặc b) một điểm A rồi từ đó chọn một đường thẳng qua A và song song với b (hoặc a)
*) Chú ý: Các định lý hay sử dụng
4.2. Dạng 2: Khoảng cách giữa hai đường thẳng chéo nhau
5. BÀI TẬP QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
Dưới đây là tổng hợp một số bài tập hay nhất của chuyên đề, các bạn có thể tải về và in ra để thuận tiện hơn cho việc làm bài tập.

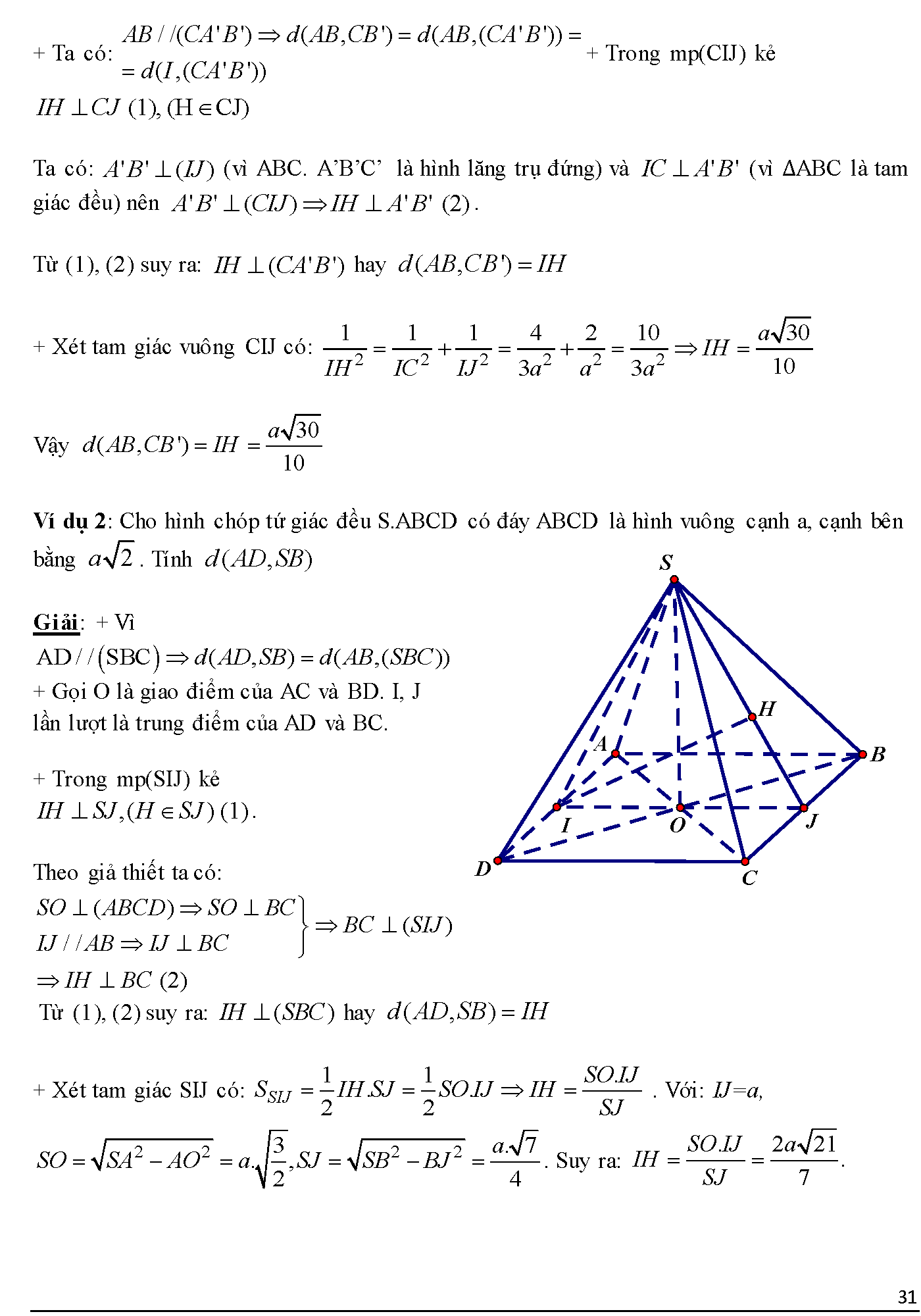
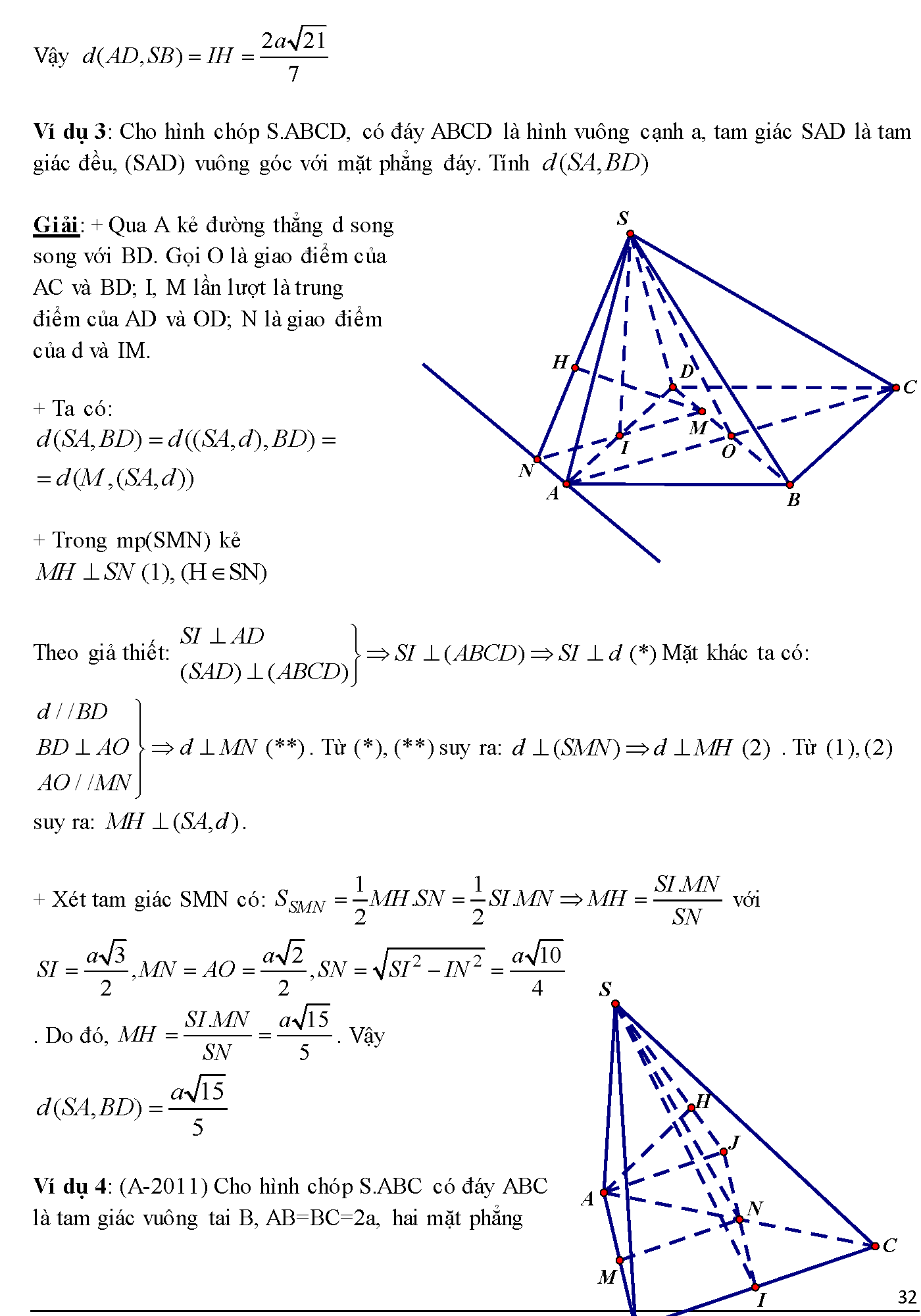




Vậy là chúng ta vừa tìm hiểu xong tất tần tật các dạng bài tập về quan hệ vuông góc trong không gian. Đối với hình học không gian thì phương pháp học tập tốt nhất vẫn là làm thật nhiều bài tập. Có bạn học sinh từng nói, hình học không gian bản chất là tưởng tượng. Do đó, làm nhiều bài tập sẽ hình thành tư duy từ đó giúp các bạn học sinh tưởng tượng tốt hơn, gải quyết bài toán một cách nhanh chóng hơn. Chúc các bạn học thật tốt chuyên đề này.




 056.3753648
056.3753648
 Chat FB
Chat FB