Tóm tắt tài liệu
Giới hạn hàm số là một chuyên đề khá quen thuộc trong chương trình toán trung học phổ thông. Để giúp các em hệ thống lại kiến thức giới hạn một cách chi tiết nhất, Tài Liệu Rẻ xin giới thiệu đến các em bài viết về phương pháp tính giới hạn hàm số.
Phương pháp tính giới hạn hàm số qua các bài toán
Bài toán 1: Tìm \[\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)\] biết \[f(x)\] xác định tại \[{{x}_{0}}\].
Bài toán 2: Tìm \[\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f(x)}{g(x)}\] trong đó \[f({{x}_{0}})=g({{x}_{0}})=0\] (dạng vô định \[\frac{0}{0}\])
Bài toán 3: Tìm \[\underset{x\to \infty }{\mathop{\lim }}\,\frac{f(x)}{g(x)}\] trong đó \[f(x),g(x)\to \infty \] (dạng \[\frac{\infty }{\infty }\])
Bài toán 4: Dạng vô định \[\infty -\infty \] và \[0.\infty \]
Bài toán 5: Dạng vô định của các hàm lượng giác.
Tính giới hạn hàm số lượng giác
Dưới đây là một vài ví dụ mẫu về tính giới hạn trong tài liệu, các em có thể tải tài liệu để xem chi tiết
Tính giới hạn các hàm số lượng giác sau
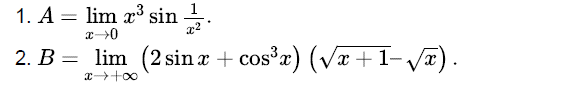

Ngoài các phương pháp giải tự luận như trên, các em hoàn toàn có thể tính giới hạn bằng một số thủ thuật casio được giới thiệu trong bài viết tính giới hạn bằng casio. Bài viết có sử dụng kiến thức từ trang toanmath.com




 056.3753648
056.3753648
 Chat FB
Chat FB